Analyse – Meervoudige integralen

Herhaling van de bepaalde integraal

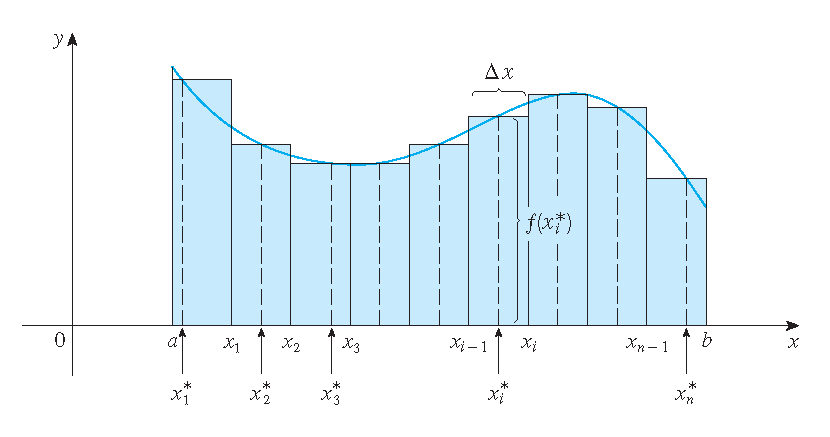
Beschouw de Riemann som

\[\sum_{i=1}^nf(x_i^*)(x_i-x_{i-1})\quad\textrm{met}\quad x_i-x_{i-1}=\Delta x=\frac{b-a}{n}.\]

Dan geldt: \(\displaystyle\int_a^bf(x)\,dx=\lim\limits_{n\to\infty}\sum_{i=1}^nf(x_i^*)\Delta x\).

Volumes en tweevoudige integralen

Evenzo, beschouw een functie \(f\) van twee variabelen gedefinieerd op een gesloten rechthoek

\[R=[a,b]\times[c,d]=\{(x,y)\,|\,a\leq x\leq b,\;c\leq y\leq d\}\]

en neem eerst aan dat \(f(x,y)\geq0\). De grafiek van \(f\) is een oppervlak met vergelijking \(z=f(x,y)\).

Laat \(S\) het lichaam zijn dat boven \(R\) ligt en onder de grafiek van \(f\), dat wil zeggen

\[S=\{(x,y,z)\in\mathbb{R}^3\,|\,0\leq z\leq f(x,y),\;(x,y)\in R\}.\]

Nu willen we het volume van \(S\) bepalen.

De eerste stap is het verdelen van de rechthoek \(R\) in deelrechthoeken. Dit wordt gedaan door het interval \([a,b]\) te verdelen in \(m\) deelintervallen \([x_{i-1},x_i]\) van gelijke breedte \(\Delta x=(b-a)/m\) en door het interval \([c,d]\) te verdelen in \(n\) deelintervallem \([y_{j-1},y_j]\) van gelijke breedte \(\Delta y=(d-c)/n\).

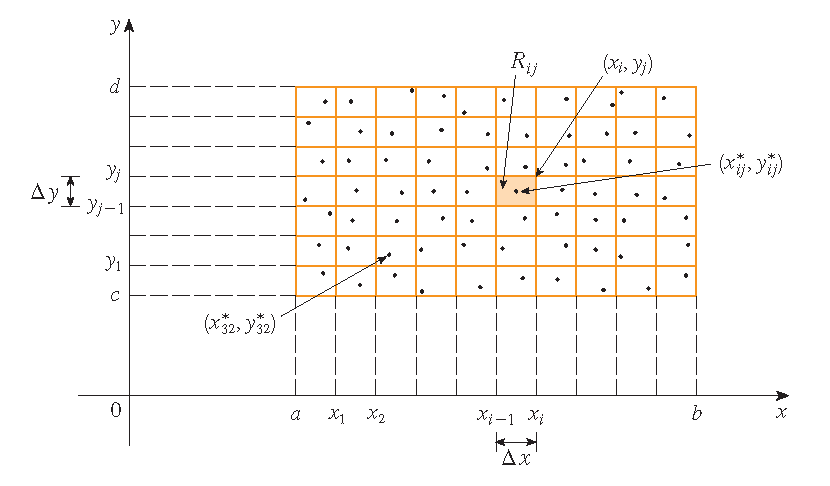
Beschouw de deelrechthoeken

\[R_{ij}=[x_{i-1},x_i]\times[y_{j-1},y_j]=\{(x,y)\,|\,x_{i-1}\leq x\leq x_i,\;y_{j-1}\leq y\leq y_j\},\]

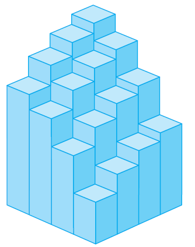
elk met oppervlakte \(\Delta A=\Delta x\,\Delta y\). Kiezen we nu een strooipunt \((x_{ij}^*,y_{ij}^*)\) in elke deelrechthoek \(R_{ij}\), dan kan het volume van \(S\) worden benaderd door de som van de volumes van rechthoekige boxen met hoogte \(f(x_{ij}^*,y_{ij}^*)\):

\[\sum_{i=1}^m\sum_{j=1}^nf(x_{ij}^*,y_{ij}^*)\Delta A.\]

Dit heet een dubbele Riemannsom.

Definitie: De tweevoudige integraal van \(f\) over de rechthoek \(R\) is

\[\iint\limits_Rf(x,y)\,dA=\lim\limits_{m\to\infty}\lim\limits_{n\to\infty}\sum_{i=1}^m\sum_{j=1}^nf(x_{ij}^*,y_{ij}^*)\Delta A.\]

---

Laatst gewijzigd op 25 september 2021