Calculus – Multiple integrals

Review of the definite integral

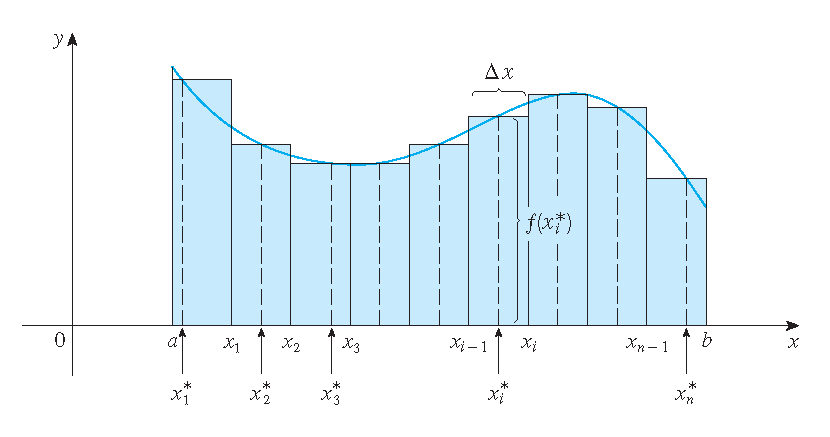
Consider the Riemann sum

\[\sum_{i=1}^nf(x_i^*)(x_i-x_{i-1})\quad\textrm{with}\quad x_i-x_{i-1}=\Delta x=\frac{b-a}{n}.\]

Then we have: \(\displaystyle\int_a^bf(x)\,dx=\lim\limits_{n\to\infty}\sum_{i=1}^nf(x_i^*)\Delta x\).

Volumes and double integrals

Similarly, consider a function \(f\) of two variables defined on a closed rectangle

\[R=[a,b]\times[c,d]=\{(x,y)\,|\,a\leq x\leq b,\;c\leq y\leq d\}\]

and first suppose that \(f(x,y)\geq0\). The graph of \(f\) is a surface with equation \(z=f(x,y)\).

Let \(S\) be the solid that lies above \(R\) and under the graph of \(f\), that is

\[S=\{(x,y,z)\in\mathbb{R}^3\,|\,0\leq z\leq f(x,y),\;(x,y)\in R\}.\]

Now we want to find the volume of \(S\).

The first step is to divide the rectangle \(R\) into subrectangles. This is accomplished by dividing the interval \([a,b]\) into \(m\) subintervals \([x_{i-1},x_i]\) of equal width \(\Delta x=(b-a)/m\) and dividing the interval \([c,d]\) into \(n\) subintervals \([y_{j-1},y_j]\) of equal width \(\Delta y=(d-c)/n\).

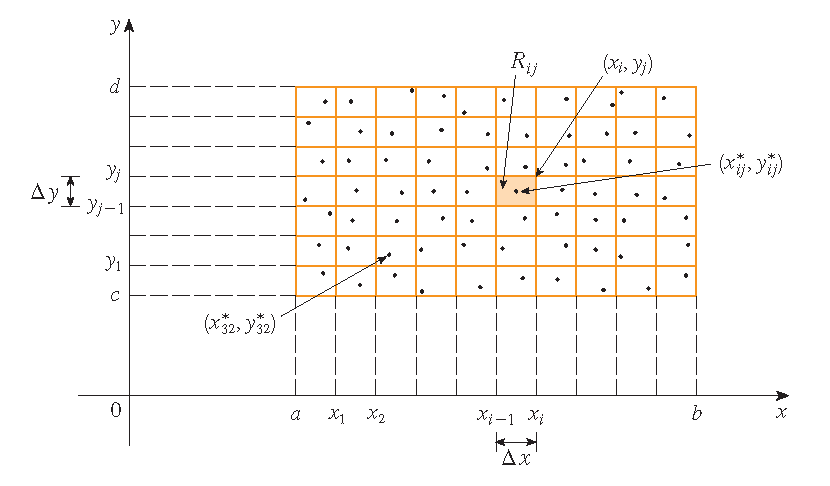
Consider the subrectangles

\[R_{ij}=[x_{i-1},x_i]\times[y_{j-1},y_j]=\{(x,y)\,|\,x_{i-1}\leq x\leq x_i,\;y_{j-1}\leq y\leq y_j\},\]

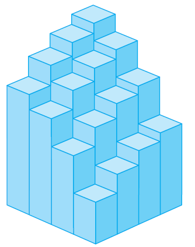
each with area \(\Delta A=\Delta x\,\Delta y\). If we choose a sample point \((x_{ij}^*,y_{ij}^*)\) in each subrectangle \(R_{ij}\), then the volume of \(S\) can be approximated by the sum of the volumes of rectangular boxes with height \(f(x_{ij}^*,y_{ij}^*)\):

\[\sum_{i=1}^m\sum_{j=1}^nf(x_{ij}^*,y_{ij}^*)\Delta A.\]

This is called a double Riemann sum.

Definition: The double integral of \(f\) over the rectangle \(R\) is

\[\iint\limits_Rf(x,y)\,dA=\lim\limits_{m\to\infty}\lim\limits_{n\to\infty}\sum_{i=1}^m\sum_{j=1}^nf(x_{ij}^*,y_{ij}^*)\Delta A.\]

---

Last modified on September 25, 2021