Analyse – Eerste orde differentiaalvergelijkingen – Separabele differentiaalvergelijkingen

Definitie: Een eerste orde differentiaalvergelijking heet separabel als deze geschreven kan worden in de vorm:

\[\frac{dy}{dx}=g(x)f(y).\]

Als \(f(y)\neq0\), dan kan dit geschreven worden als

\[\frac{dy}{dx}=g(x)f(y)=\frac{g(x)}{h(y)}\quad\text{met}\quad h(y)=\frac{1}{f(y)}.\]

Dan volgt dat

\[h(y)\,dy=g(x)\,dx\quad\Longrightarrow\quad\int h(y)\,dy=\int g(x)\,dx.\]

Deze vergelijking definieert \(y\) impliciet als een functie van \(x\).

Voorbeelden:

1) \(\displaystyle\frac{dy}{dx}=\frac{x}{y}\) met \(y\neq0\) is separabel:

\[y\,dy=x\,dx\quad\Longleftrightarrow\quad\tfrac{1}{2}y^2=\tfrac{1}{2}x^2+C\quad\Longleftrightarrow\quad y^2=x^2+K.\]

Dit is een impliciete vorm van de oplossing. Zonodig volgt hieruit de expliciete vorm \(y(x)=\pm\sqrt{x^2+K}\) met \(K\in\mathbb{R}\).

2) \(\displaystyle\frac{dy}{dx}=\frac{y}{x}\) met \(x>0\) is separabel. Merk op dat \(y=0\) een oplossing is. Voor \(y\neq0\) volgt:

\[\frac{dy}{y}=\frac{dx}{x}\quad\Longleftrightarrow\quad\ln|y(x)|=\ln|x|+C\quad\Longleftrightarrow\quad y(x)=\pm e^Cx.\]

Omdat ook \(y=0\) een oplossing is, volgt hieruit dat de algemene oplossing is: \(y(x)=Kx\) met \(K\in\mathbb{R}\).

3) \(\displaystyle\frac{dy}{dx}=2xy\) is separabel. Merk op dat \(y=0\) een oplossing is. Voor \(y\neq0\) volgt:

\[\frac{dy}{y}=2x\,dx\quad\Longleftrightarrow\quad\ln|y(x)|=x^2+C\quad\Longleftrightarrow\quad y(x)=\pm e^C\cdot e^{x^2}.\]

Omdat ook \(y=0\) een oplossing is, volgt hieruit dat de algemene oplossing is: \(y(x)=Ke^{x^2}\) met \(K\in\mathbb{R}\).

4) \(\displaystyle\frac{dy}{dx}=2x(1+y^2)\) is separabel:

\[\frac{dy}{1+y^2}=2x\,dx\quad\Longleftrightarrow\quad\arctan(y)=x^2+C\quad\Longleftrightarrow\quad y=\tan(x^2+C).\]

De algemene oplossing is dus: \(y(x)=\tan(x^2+C)\) met \(C\in\mathbb{R}\).

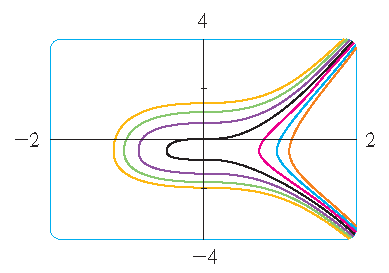
5) Stewart §9.3, Voorbeeld 2: \(\displaystyle\frac{dy}{dx}=\frac{6x^2}{2y+\cos(y)}\) is separabel:

\[(2y+\cos(y))\,dy=6x^2\,dx\quad\Longleftrightarrow\quad y^2+\sin(y)=2x^3+C.\]

Deze familie van impliciet gegeven oplossingen kan worden weergegeven in een plaatje:

Een voorbeeld van de methode van Feynman (zie: de methode van Feynman)

Beschouw de integraal \(I(t)=\displaystyle\int_0^{\infty}e^{-x^2}\cos(xt)\,dx\). Dan volgt: \(I(0)=\displaystyle\int_0^{\infty}e^{-x^2}\,dx=\tfrac{1}{2}\sqrt{\pi}\) (zie: de normale verdeling) en

\begin{align*} I'(t)&=-\int_0^{\infty}xe^{-x^2}\sin(xt)\,dx=\frac{1}{2}\int_0^{\infty}\sin(xt)\,de^{-x^2} =\frac{1}{2}e^{-x^2}\sin(xt)\bigg|_0^{\infty}-\frac{1}{2}\int_0^{\infty}e^{-x^2}\,d\sin(xt)\\[2.5mm] &=0-\frac{1}{2}t\int_0^{\infty}e^{-x^2}\cos(xt)\,dx=-\frac{1}{2}tI(t). \end{align*}

Dit is een separabele differentiaalvergelijking met algemene oplossing \(I(t)=ce^{-\frac{1}{4}t^2}\). Nu volgt \(c=I(0)=\frac{1}{2}\sqrt{\pi}\). Dus: \(I(t)=\frac{1}{2}\sqrt{\pi}e^{-\frac{1}{4}t^2}\).

---

Laatst gewijzigd op 20 april 2024