OnderwijsAnalyse – Eerste orde differentiaalvergelijkingen – Toepassingen
Populatiegroei
De logistische differentiaalvergelijking \(\displaystyle\frac{dP}{dt}=kP\left(1-\frac{P}{M}\right)\) is separabel. Merk op dat \(P(t)=0\)
en \(P(t)=M\) twee constante oplossingen zijn, die evenwichtsoplossingen worden genoemd. Voor \(P\neq0\) en \(P\neq M\) geldt:
Nu gebruiken we de partiële breuksplitsing \(\displaystyle\frac{M}{P(M-P)}=\frac{1}{P}+\frac{1}{M-P}\):
\[\int\frac{M}{P(M-P)}\,dP=\int\left(\frac{1}{P}+\frac{1}{M-P}\right)\,dP=\ln|P|-\ln|M-P|+\text{a constant.}\]Dus geldt:
\[\ln\left|\frac{P}{M-P}\right|=kt+C\quad\Longrightarrow\quad\frac{M-P}{P}=\pm e^{-C}\cdot e^{-kt}.\]Merk op dat \(\pm e^{-C}\) een willekeurige positieve of negatieve constante is. Als we dit vervangen door een willekeurige constante \(K\) dan krijgen we de "verloren" constante oplossing \(P=M\) weer terug: \(\displaystyle\frac{M-P}{P}=Ke^{-kt}\). Dit is een impliciete vorm van de oplossing. Als we dit oplossien voor \(P\) dan volgt \(P(t)=\displaystyle\frac{M}{1+Ke^{-kt}}\). Voor een beginvoorwaarde \(P(0)=P_0>0\) volgt dan dat \(K=\displaystyle\frac{M-P_0}{P_0}\). We concluderen dus dat
\[P(t)=\frac{M}{1+Ke^{-kt}}\quad\text{met}\quad K=\frac{M-P_0}{P_0}.\]De koelingswet van Newton
De koelingswet van Newton zegt dat the snelheid waarmee een object afkoelt evenredig is met het temperatuurverschil tussen dat van het object
en dat van de omgeving, mits dit verschil niet te groot is. Laat \(T(t)\) de temperatuur zijn van een object op tijdstip \(t\)en \(T_s\) de
temperatuur van de omgeving, dan kan deze wet worden geschreven als:
waarbij \(T_0\) de temperatuur van het object is op tijdstip \(t=0\). Hier heet\(T(0)=T_0\) de beginvoorwaarde.
Omdat \(T_s\) constant is, leidt de substitutie \(y(t)=T(t)-T_s\) eenvoudig tot de oplossing:
\[T(t)=T_s+(T_0-T_s)e^{kt}.\]Echter, merk op dat de differentiaalvergelijking separabel is en dat \(T(t)=T_s\) een (constante) oplossing is. Voor \(T(t)\neq T_s\) geldt:
\[\frac{dT}{T-T_s}=k\,dt\quad\Longrightarrow\quad\ln|T-T_s|=kt+C\quad\Longrightarrow\quad T(t)-T_s=\pm e^C\cdot e^{kt}.\]Omdat \(T(t)=T_s\) ook een oplossing is, concluderen we dat de algemene oplossing \(T(t)-T_s=Ke^{kt}\) met \(K\in\mathbb{R}\) is. Nu leidt de beginvoorwaarde \(T(0)=T_0\) tot \(K=T_0-T_s\). Dus geldt: \(T(t)=T_s+(T_0-T_s)e^{kt}\).
Voorbeelden
1) Een fles frisdrank met een temperatuur van \(20^{\circ}\;\text{C}\) wordt in een koelkast geplaatst waar de temperatuur \(5^{\circ}\;\text{C}\) is. Na een half uur is de frisdrank gekoeld tot \(15^{\circ}\;\text{C}\).
- Wat is de temperatuur van de frisdrank na een half uur?
- Hoelang duurt het tot de frisdrank is afgekoeld tot \(10^{\circ}\;\text{C}\)?
Merk op dat hier \(T_s=5\) en \(T(0)=20\). Dus geldt:
\[\frac{dT}{dt}=k(T-5),\quad T(0)=20\quad\Longrightarrow\quad T(t)=5+15e^{kt}.\]Als we minuten kiezen als eenheid voor de tijd \(t\), dan volgt dat
\[T(30)=15\quad\Longleftrightarrow\quad 15=5+15e^{30k}\quad\Longleftrightarrow\quad 30k=\ln\left(\frac{10}{15}\right).\]Hieruit volgt dat \(k=\frac{1}{30}\ln\left(\frac{2}{3}\right)\approx−0.0135\). Dan volgt:
- \(T(60)=5+15e^{−0.0135\cdot60}\approx11.7^{\circ}\;\text{C}\).
- \(T(t)=10\;\Longleftrightarrow\;10=5+15e^{−0.0135t}\quad\Longleftrightarrow\quad−0.0135t=\ln\left(\frac{5}{15}\right)\).
Hieruit volgt dat het ongeveer \(\displaystyle\frac{\ln\left(\frac{1}{3}\right)}{−0.0135}\approx81.4\) minuten duurt tot de frisdrank is afgekoeld tot \(10^{\circ}\;\text{C}\).
2) Een kop koffie met een temperatuur van \(95^{\circ}\;\text{C}\) wordt geplaatst in een ruimte waar de temperatuur \(20^{\circ}\;\text{C}\) is. Na \(10\) minuten is de koffie afgekoeld tot \(75^{\circ}\;\text{C}\).
- Wat is de temperatuur van de koffie na \(15\) minutes?
- Hoelang duurt het tot de koffie is afgekoeld tot \(80^{\circ}\;\text{C}\)?
Merk op dat hier \(T_s=20\) en \(T(0)=95\). Dus geldt:
\[\frac{dT}{dt}=k(T-20),\quad T(0)=95\quad\Longrightarrow\quad T(t)=20+75e^{kt}.\]Merk op dat
\[T(10)=75\quad\Longleftrightarrow\quad 75=20+75e^{10k}\quad\Longleftrightarrow\quad 10k=\ln\left(\frac{55}{75}\right).\]Hieruit volgt dat \(k=\frac{1}{10}\ln\left(\frac{11}{15}\right)\approx−0.031\). Dan volgt:
- \(T(15)=20+75e^{−0.031\cdot15}\approx67^{\circ}\;\text{C}\).
- \(T(t)=80\;\Longleftrightarrow\;80=20+75e^{−0.031t}\quad\Longleftrightarrow\quad−0.031t=\ln\left(\frac{60}{75}\right)\).
Hieruit volgt dat het ongeveer \(\displaystyle\frac{\ln\left(\frac{4}{5}\right)}{−0.031}\approx7.2\) minuten duurt tot de koffie is afgekoeld tot \(80^{\circ}\;\text{C}\).
De wet van Torricelli
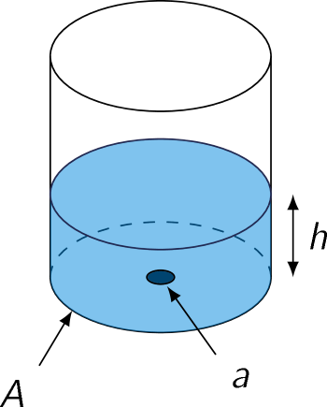De wet van Torricelli, ook wel de stelling van Torricelli, is een stelling in de vloeistofdynamica die de snelheid van een vloeistof die uit een
opening stroomt relateert aan de hoogte van de vloeistof boven het gat. De wet zegt dat de uitstroomsnelheid \(v\) van een vloeistof dat door
een gat met scherpe randen in de bodem van een vat, dat tot een diepte \(h\) is gevuld, stroomt gelijk is aan de snelheid dat een lichaam (in
dit geval een waterdruppel) zou verkrijgen als dit vrij zou vallen vanaf een hoogte \(h\), d.w.z. \(v=\sqrt{2gh}\), waarbij \(g\) de versnelling
van de zwaartekracht (\(981\;\text{cm}/\text{s}^2\) is in de buurt van de oppervlak van de aarde).
Beschouw nu een cilindrische tank met een gat met oppervlakte \(a\) in de bodem (zie het plaatje) en neem aan dat er water stroomt uit het gat. Als \(V(t)\) het volume van het water weergeeft op tijdstip \(t\), dan leidt de wet van Torricelli tot:
\[\frac{dV}{dt}=-a\sqrt{2gh}.\]Als de oppervlakte van de dwarsdoorsnede van de tank gelijk is aan \(A\), dan geldt:
\[A\frac{dh}{dt}=-a\sqrt{2gh}.\]Merk op dat dit een separabele differentiaalvergelijking is.
Als de straal van de tank gelijk is aan \(10\;\text{cm}\), de straal van het gat \(1\;\text{cm}\) en de hoogte van het water \(10;\text{cm}\), dan is
\[A=100\pi\;\text{cm}^3,\quad a=\pi\;\text{cm}^3\quad\text{en}\quad h=10\;\text{cm}.\]Hoelang duurt het tot het water volledig is weggestroomd?
We willen dus het beginwaardeprobleem
\[100\frac{dh}{dt}=-\sqrt{2gh},\quad h(0)=10\]oplossen, Merk op dat \(h(t)=0\) een (constante) oplossing van de differentiaalvergelijking is. Voor \(h(t)\neq0\) vinden we
\[100\frac{dh}{\sqrt{h}}=-\sqrt{2g}\,dt\quad\Longrightarrow\quad 200\sqrt{h}=-\sqrt{2g}t+C.\]Uit de beginvoorwaarde \(h(0)=10\) volgt dat \(C=200\sqrt{10}\). Hieruit volgt dat de oplossing geschreven kan worden als
\[h(t)=\left(\frac{200\sqrt{10}-\sqrt{2g}t}{200}\right)^2.\]Nu kunnen we de vraag beantwoorden: \(h(t)=0\;\Longleftrightarrow\;t=\displaystyle\frac{200\sqrt{10}}{\sqrt{2g}}\). Hieruit volgt dat de tank na \(\displaystyle\frac{200\sqrt{10}}{\sqrt{2g}}\approx14.3\) seconden leeg zal zijn.
Leercurve (Stewart §9.5, Opgave 31)
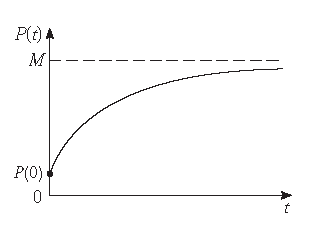
Laat \(P(t)\) het prestatieniveau zijn van iemand die een vaardigheid leert als functie van de trainingstijd \(t\). De grafiek van \(P\) heet een
leercurve.
Als \(M\) het maximale prestatieniveau is waartoe een leerling in staat zou kunnen zijn, dan is
\[\frac{dP}{dt}=k(M-P)\]een redelijk model voor het leren (zie: Stewart §9.1, Opgave 15), waarbij \(k\) een positieve constante is.
Merk op dat deze differentiaalvergelijking lineair is. We zoeken dus een integrerende factor \(I(t)\):
\[I(t)P'(t)+kI(t)P(t)=kMI(t)\quad\text{with}\quad I'(t)=kI(t)\quad\Longrightarrow\quad I(t)=e^{kt}\;\text{for instance}.\]Hieruit volgt dat
\[\frac{d}{dt}\left[e^{kt}P(t)\right]=kMe^{kt}\quad\Longrightarrow\quad e^{kt}P(t)=\int kMe^{kt}\,dt=Me^{kt}+C.\]Dus gledt: \(P(t)=M+Ce^{-kt}\).
Vrije val
Als een skydiver uit een vliegtuig springt zonder beginsnelheid, dan zal de luchtweerstand evenredig zijn aan zijn snelheid. Een model voor de
snelheid van de skydiver is:
\(m\displaystyle\frac{dv}{dt}=mg-kv,\quad v(0)=0\),
waarbij \(m\) de massa van de skydiver is, \(g=9.81\;\text{m}/\text{s}^2\) de versnelling van de zwaartekracht en \(k\) een positieve constante.
Neem aan dat \(m=90\;\text{kg}\) en \(k=15\), dan geldt:
\[90\frac{dv}{dt}=90g-15v\quad\Longleftrightarrow\quad v'(t)+\tfrac{1}{6}v(t)=g.\]Dit is een lineaire differentiaalvergelijking. Met behulp van de integrerende factor \(e^{\frac{1}{6}t}\) volgt dan dat:
\[\frac{d}{dt}\left[e^{\frac{1}{6}t}v(t)\right]=ge^{\frac{1}{6}t}\quad\Longrightarrow\quad e^{\frac{1}{6}t}v(t)=6ge^{\frac{1}{6}t}+C \quad\Longrightarrow\quad v(t)=6g+Ce^{-\frac{1}{6}t}.\]Uit de beginvoorwaarde \(v(0)=0\) volgt dan dat \(C=-6g\). Dus geldt: \(v(t)=6g\left(1-e^{-\frac{1}{6}t}\right)\).
Met \(6g=6\cdot9.8=58.8\), volgt hieruit bijvoorbeeld dat de snelheid van de skydiver na \(10\) seconden gelijk is aan: \(v(10)=58.8\left(1-e^{-\frac{5}{3}}\right)\approx47.7\;\text{m}/\text{s}\).
Verder, omdat \(v(t)=50\;\Longleftrightarrow\displaystyle\;t=-6\ln\left(\frac{8.8}{58.8}\right)\approx11.4\) concluderen we dat het ongeveer \(11.4\) seconden duurt tot een snelheid van \(50\;\text{m}/\text{s}\) (dat is \(180\;\text{km}/\text{h}\)) wordt bereikt.
Ten slotte, als de vrije val eeuwig zou kunnen duren, dan zou de (theoretische) maximumsnelheid \(\lim\limits_{t\to\infty}v(t)=58.8\;\text{m}/\text{s}\) zijn. Oplossen van
\[v(t)=58\quad\Longleftrightarrow\quad t=-6\ln\left(\frac{0.8}{58.8}\right)\approx25.8.\]leidt tot de conclusie dat het ongeveer \(25.8\) seconden duurt tot een snelheid van \(58\;\text{m}/\text{s}\) (dat is \(208.8\;\text{km}/\text{h}\)) wordt bereikt.
Laatst gewijzigd op 8 maart 2021
