TeachingCalculus – First-order differential equations – Applications
Population growth
The logistic differential equation \(\displaystyle\frac{dP}{dt}=kP\left(1-\frac{P}{M}\right)\) is separable. Observe that \(P(t)=0\)
and \(P(t)=M\) are two constant solutions, which are called equilibrium solutions. For \(P\neq0\) and \(P\neq M\) we have:
Now we use the partial fraction decomposition \(\displaystyle\frac{M}{P(M-P)}=\frac{1}{P}+\frac{1}{M-P}\) to find that
\[\int\frac{M}{P(M-P)}\,dP=\int\left(\frac{1}{P}+\frac{1}{M-P}\right)\,dP=\ln|P|-\ln|M-P|+\text{a constant.}\]Hence we have:
\[\ln\left|\frac{P}{M-P}\right|=kt+C\quad\Longrightarrow\quad\frac{M-P}{P}=\pm e^{-C}\cdot e^{-kt}.\]Note that \(\pm e^{-C}\) is an arbitrary positive or negative constant. If we replace this by an arbitrary constant \(K\) we retrieve the "lost" constant solution \(P=M\): \(\displaystyle\frac{M-P}{P}=Ke^{-kt}\). This is an implicit form of the solution. Solving for \(P\) we obtain \(P(t)=\displaystyle\frac{M}{1+Ke^{-kt}}\). For an initial condition \(P(0)=P_0>0\) we find that \(K=\displaystyle\frac{M-P_0}{P_0}\). So we conclude that
\[P(t)=\frac{M}{1+Ke^{-kt}}\quad\text{with}\quad K=\frac{M-P_0}{P_0}.\]Newton's law of cooling
Newton's law of cooling states that the rate of cooling of an object is proportional to the temperature difference between the object and its
surroundings, provided that this difference is not too large. Let \(T(t)\) be the temperature of the object at time \(t\) and \(T_s\) the
temperature of the surroundings, then this law can be written as:
where \(T_0\) denotes the temperature of the object at time \(t=0\). Here \(T(0)=T_0\) is called the initial condition.
Since \(T_s\) is constant, the substitution \(y(t)=T(t)-T_s\) easily leads to the solution:
\[T(t)=T_s+(T_0-T_s)e^{kt}.\]However, note that the differential equation is separable and that \(T(t)=T_s\) is a (constant) solution. For \(T(t)\neq T_s\) we have:
\[\frac{dT}{T-T_s}=k\,dt\quad\Longrightarrow\quad\ln|T-T_s|=kt+C\quad\Longrightarrow\quad T(t)-T_s=\pm e^C\cdot e^{kt}.\]Since \(T(t)=T_s\) is a solution too, we conclude that the general solution is \(T(t)-T_s=Ke^{kt}\) with \(K\in\mathbb{R}\). Now the initial condition \(T(0)=T_0\) leads to \(K=T_0-T_s\). Hence we have: \(T(t)=T_s+(T_0-T_s)e^{kt}\).
Examples
1) A bottle of soda pop with a temperature of \(20^{\circ}\;\text{C}\) is placed in a refrigerator where the temperature is \(5^{\circ}\;\text{C}\). After half an hour the soda pop has cooled to \(15^{\circ}\;\text{C}\).
- What is the temperature of the soda pop after one hour?
- How long does it take for the soda pop to cool to \(10^{\circ}\;\text{C}\)?
Note that \(T_s=5\) and \(T(0)=20\) here. So we have:
\[\frac{dT}{dt}=k(T-5),\quad T(0)=20\quad\Longrightarrow\quad T(t)=5+15e^{kt}.\]If we choose to take minutes for the time \(t\), we conclude that
\[T(30)=15\quad\Longleftrightarrow\quad 15=5+15e^{30k}\quad\Longleftrightarrow\quad 30k=\ln\left(\frac{10}{15}\right).\]This implies that \(k=\frac{1}{30}\ln\left(\frac{2}{3}\right)\approx−0.0135\). Then we have:
- \(T(60)=5+15e^{−0.0135\cdot60}\approx11.7^{\circ}\;\text{C}\).
- \(T(t)=10\;\Longleftrightarrow\;10=5+15e^{−0.0135t}\quad\Longleftrightarrow\quad−0.0135t=\ln\left(\frac{5}{15}\right)\).
This implies that it takes approximately \(\displaystyle\frac{\ln\left(\frac{1}{3}\right)}{−0.0135}\approx81.4\) minutes for the soda pop to cool to \(10^{\circ}\;\text{C}\).
2) A cup of coffee with a temperature of \(95^{\circ}\;\text{C}\) is placed in a room where the temperature is \(20^{\circ}\;\text{C}\). After \(10\) minutes the coffee has cooled to \(75^{\circ}\;\text{C}\).
- What is the temperature of the coffee after \(15\) minutes?
- How long does it take for the coffee to cool to \(80^{\circ}\;\text{C}\)?
Note that \(T_s=20\) and \(T(0)=95\) here. So we have:
\[\frac{dT}{dt}=k(T-20),\quad T(0)=95\quad\Longrightarrow\quad T(t)=20+75e^{kt}.\]Note that
\[T(10)=75\quad\Longleftrightarrow\quad 75=20+75e^{10k}\quad\Longleftrightarrow\quad 10k=\ln\left(\frac{55}{75}\right).\]This implies that \(k=\frac{1}{10}\ln\left(\frac{11}{15}\right)\approx−0.031\). Then we have:
- \(T(15)=20+75e^{−0.031\cdot15}\approx67^{\circ}\;\text{C}\).
- \(T(t)=80\;\Longleftrightarrow\;80=20+75e^{−0.031t}\quad\Longleftrightarrow\quad−0.031t=\ln\left(\frac{60}{75}\right)\).
This implies that it takes approximately \(\displaystyle\frac{\ln\left(\frac{4}{5}\right)}{−0.031}\approx7.2\) minutes for the coffee to cool to \(80^{\circ}\;\text{C}\).
Torricelli's law
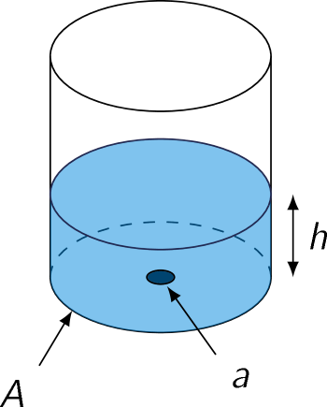Torricelli's law, also known as Torricelli's theorem, is a theorem in fluid dynamics relating the speed of fluid flowing out of an orifice to the height
of the fluid above the hole. The law states that the speed of efflux \(v\) of a fluid through a sharp-edged hole at the bottom of a tank filled to a
depth \(h\) is the same as the speed that a body (in this case a drop of water) would acquire in falling freely from a height \(h\), i.e.
\(v=\sqrt{2gh}\), where \(g\) is the acceleration due to gravity (\(981\;\text{cm}/\text{s}^2\) near the surface of the earth).
Now consider a cylindrical tank that has a hole with area \(a\) in its bottom (see the picture) and assume that water is draining from the hole. If \(V(t)\) denotes the volume of the water at time \(t\), then Torricelli's law leads to:
\[\frac{dV}{dt}=-a\sqrt{2gh}.\]If the cross-sectional area of the tank is \(A\), then we have:
\[A\frac{dh}{dt}=-a\sqrt{2gh}.\]Note that this is a separable differential equation.
If the radius of the tank is \(10\;\text{cm}\), the radius of the hole is \(1\;\text{cm}\) and the height of the water is \(10;\text{cm}\), then
\[A=100\pi\;\text{cm}^3,\quad a=\pi\;\text{cm}^3\quad\text{and}\quad h=10\;\text{cm}.\]How long does it take for the water to drain completely?
So we want to solve the initial-value problem:
\[100\frac{dh}{dt}=-\sqrt{2gh},\quad h(0)=10.\]Note that \(h(t)=0\) is a (constant) solution of the differential equation. For \(h(t)\neq0\) we obtain
\[100\frac{dh}{\sqrt{h}}=-\sqrt{2g}\,dt\quad\Longrightarrow\quad 200\sqrt{h}=-\sqrt{2g}t+C.\]The initial condition \(h(0)=10\) leads to \(C=200\sqrt{10}\). This implies that the solution can be written as
\[h(t)=\left(\frac{200\sqrt{10}-\sqrt{2g}t}{200}\right)^2.\]Now we can answer the question: \(h(t)=0\;\Longleftrightarrow\;t=\displaystyle\frac{200\sqrt{10}}{\sqrt{2g}}\). This implies that the tank will be empy after \(\displaystyle\frac{200\sqrt{10}}{\sqrt{2g}}\approx14.3\) seconds.
Learning curve (Stewart §9.5, Exercise 31)
Let \(P(t)\) be the performance level of someone learning a skill as a function of the training time \(t\). The graph of \(P\) is called a
learning curve.
If \(M\) is the maximum level of performance of which the learner is capable, then
\[\frac{dP}{dt}=k(M-P)\]is a a reasonable model for learning (see: Stewart §9.1, Exercise 15), where \(k\) is a positive constant.
Note that this differential equation is linear. So we look for an integrating factor \(I(t)\):
\[I(t)P'(t)+kI(t)P(t)=kMI(t)\quad\text{with}\quad I'(t)=kI(t)\quad\Longrightarrow\quad I(t)=e^{kt}\;\text{for instance}.\]This implies that
\[\frac{d}{dt}\left[e^{kt}P(t)\right]=kMe^{kt}\quad\Longrightarrow\quad e^{kt}P(t)=\int kMe^{kt}\,dt=Me^{kt}+C.\]Hence we have: \(P(t)=M+Ce^{-kt}\).
Free fall
If a skydiver jumps out of a plane with no initial velocity, the air resistance will be proportional to its velocity. A model for the velocity of the
skydiver is:
\(m\displaystyle\frac{dv}{dt}=mg-kv,\quad v(0)=0\),
where \(m\) denotes the mass of the skydiver, \(g=9.81\;\text{m}/\text{s}^2\) is the acceleration due to gravity and \(k\) is a positive constant.
Assume that \(m=90\;\text{kg}\) and \(k=15\), then we have:
\[90\frac{dv}{dt}=90g-15v\quad\Longleftrightarrow\quad v'(t)+\tfrac{1}{6}v(t)=g.\]This is a linear differential equation. Using the integrating factor \(e^{\frac{1}{6}t}\) we find that:
\[\frac{d}{dt}\left[e^{\frac{1}{6}t}v(t)\right]=ge^{\frac{1}{6}t}\quad\Longrightarrow\quad e^{\frac{1}{6}t}v(t)=6ge^{\frac{1}{6}t}+C \quad\Longrightarrow\quad v(t)=6g+Ce^{-\frac{1}{6}t}.\]Now we use the initial condition \(v(0)=0\) to find that \(C=-6g\). Hence we have: \(v(t)=6g\left(1-e^{-\frac{1}{6}t}\right)\).
Using \(6g=6\cdot9.8=58.8\), for instance this implies that the speed of the skydiver after \(10\) seconds is: \(v(10)=58.8\left(1-e^{-\frac{5}{3}}\right)\approx47.7\;\text{m}/\text{s}\).
Furthermore, since \(v(t)=50\;\Longleftrightarrow\displaystyle\;t=-6\ln\left(\frac{8.8}{58.8}\right)\approx11.4\) we conclude that it takes approximately \(11.4\) seconds to reach a speed of \(50\;\text{m}/\text{s}\) (which is \(180\;\text{km}/\text{h}\)).
Finally, if the free fall could last forever, the (theoretical) maximum speed would be \(\lim\limits_{t\to\infty}v(t)=58.8\;\text{m}/\text{s}\). Solving
\[v(t)=58\quad\Longleftrightarrow\quad t=-6\ln\left(\frac{0.8}{58.8}\right)\approx25.8.\]we conclude that it takes approximately \(25.8\) seconds to reach a speed of \(58\;\text{m}/\text{s}\) (which is \(208.8\;\text{km}/\text{h}\)).
Last modified on March 8, 2021
