Calculus – First-order differential equations – Separable differential equations

Definition: A first-order differentail equation is called separable if it can be written in the form:

\[\frac{dy}{dx}=g(x)f(y).\]

If \(f(y)\neq0\), then this can be written as

\[\frac{dy}{dx}=g(x)f(y)=\frac{g(x)}{h(y)}\quad\text{with}\quad h(y)=\frac{1}{f(y)}.\]

Then we have

\[h(y)\,dy=g(x)\,dx\quad\Longrightarrow\quad\int h(y)\,dy=\int g(x)\,dx.\]

This equation defines \(y\) implicitly as a function of \(x\).

Examples:

1) \(\displaystyle\frac{dy}{dx}=\frac{x}{y}\) with \(y\neq0\) is separable:

\[y\,dy=x\,dx\quad\Longleftrightarrow\quad\tfrac{1}{2}y^2=\tfrac{1}{2}x^2+C\quad\Longleftrightarrow\quad y^2=x^2+K.\]

This is an implicit form of the solution. If necessary this implies the explicit form \(y(x)=\pm\sqrt{x^2+K}\) with \(K\in\mathbb{R}\).

2) \(\displaystyle\frac{dy}{dx}=\frac{y}{x}\) with \(x>0\) is separable. Note that \(y=0\) is a solution. For \(y\neq0\) we have:

\[\frac{dy}{y}=\frac{dx}{x}\quad\Longleftrightarrow\quad\ln|y(x)|=\ln|x|+C\quad\Longleftrightarrow\quad y(x)=\pm e^Cx.\]

Since \(y=0\) is a solution too, this implies that the general solution is: \(y(x)=Kx\) with \(K\in\mathbb{R}\).

3) \(\displaystyle\frac{dy}{dx}=2xy\) is separable. Note that \(y=0\) is a solution. For \(y\neq0\) we have:

\[\frac{dy}{y}=2x\,dx\quad\Longleftrightarrow\quad\ln|y(x)|=x^2+C\quad\Longleftrightarrow\quad y(x)=\pm e^C\cdot e^{x^2}.\]

Since \(y=0\) is a solution too, this implies that the general solution is: \(y(x)=Ke^{x^2}\) with \(K\in\mathbb{R}\).

4) \(\displaystyle\frac{dy}{dx}=2x(1+y^2)\) is separable:

\[\frac{dy}{1+y^2}=2x\,dx\quad\Longleftrightarrow\quad\arctan(y)=x^2+C\quad\Longleftrightarrow\quad y=\tan(x^2+C).\]

Hence the general solution is: \(y(x)=\tan(x^2+C)\) with \(C\in\mathbb{R}\).

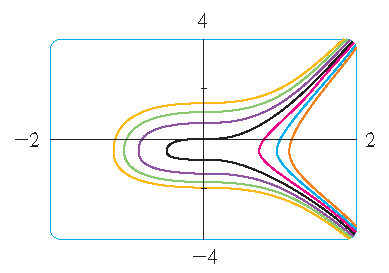
5) Stewart §9.3, Example 2: \(\displaystyle\frac{dy}{dx}=\frac{6x^2}{2y+\cos(y)}\) is separable:

\[(2y+\cos(y))\,dy=6x^2\,dx\quad\Longleftrightarrow\quad y^2+\sin(y)=2x^3+C.\]

This family of implicit given solutions can be represented in a picture:

An example of the Feynman method (see: the Feynman method)

Consider the integral \(I(t)=\displaystyle\int_0^{\infty}e^{-x^2}\cos(xt)\,dx\). Then we have: \(I(0)=\displaystyle\int_0^{\infty}e^{-x^2}\,dx=\tfrac{1}{2}\sqrt{\pi}\) (see: the normal distribution) and

\begin{align*} I'(t)&=-\int_0^{\infty}xe^{-x^2}\sin(xt)\,dx=\frac{1}{2}\int_0^{\infty}\sin(xt)\,de^{-x^2} =\frac{1}{2}e^{-x^2}\sin(xt)\bigg|_0^{\infty}-\frac{1}{2}\int_0^{\infty}e^{-x^2}\,d\sin(xt)\\[2.5mm] &=0-\frac{1}{2}t\int_0^{\infty}e^{-x^2}\cos(xt)\,dx=-\frac{1}{2}tI(t). \end{align*}

This is a separable differential equation with general soloution \(I(t)=ce^{-\frac{1}{4}t^2}\). Now we have \(c=I(0)=\frac{1}{2}\sqrt{\pi}\). Hence: \(I(t)=\frac{1}{2}\sqrt{\pi}e^{-\frac{1}{4}t^2}\).

---

Last modified on April 20, 2024