Calculus – First-order differential equations
Definition: A differential equation is an equation involving an unknown function and one or more of its derivatives. The order of the highest derivative involved is called the order of the differential equation.
For the moment we only consider first-order differential equations of the form \(\displaystyle\frac{dy}{dx}=F(x,y)\) with \(y=y(x)\).
Population growth
One model for the growth of a population is based on the assumption that the population grows at a rate proportional to the size of the population.
That is a reasonable assumption for a population of bacteria or animals under ideal conditions (unlimited environment, adequate nutrition, absence of predators, immunity of disease).
If \(P(t)\) denotes the number of individuals in a population at time \(t\), then: \(\displaystyle\frac{dP}{dt}=kP\), where \(k\) denotes the growth rate. This is called exponential growth, since the general solution is \(P(t)=Ce^{kt}\) with \(C\in\mathbb{R}\).
A more realistic model is \(\displaystyle\frac{dP}{dt}=kP\left(1-\frac{P}{M}\right)\). This is called a logistic differential equation.
This differential equation was proposed by the Belgian mathematician Pierre-François Verhulst in 1838 as a model for world population growth.
This more realistic model reflects the fact that a given environment has limited resources. Many populations start by increasing in an exponential manner, but the population levels off when it approaches its carrying capacity \(M\) (or decreases toward \(M\) if it ever exceeds \(M\)).
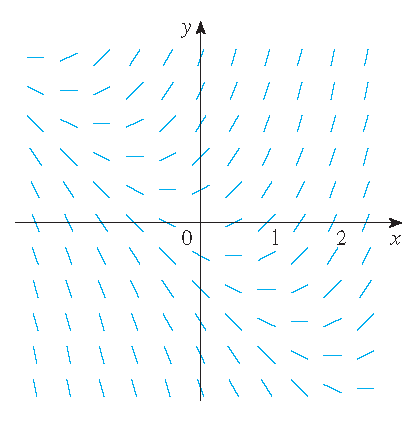
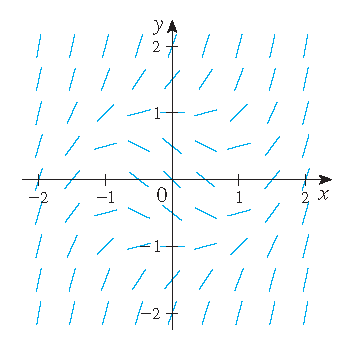
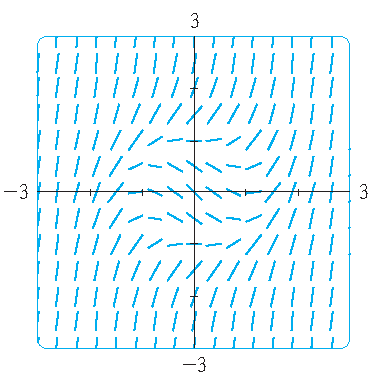
Instead of solving differential equations of the form \(\displaystyle\frac{dy}{dx}=F(x,y)\) it is possible to consider direction fields.
Examples:
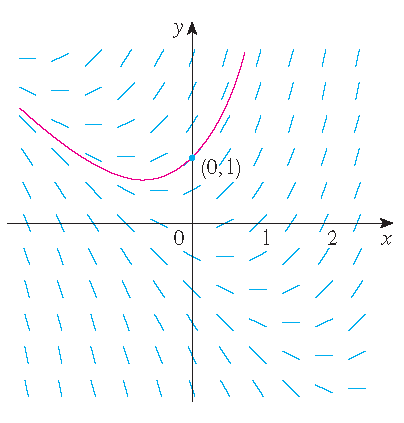
1) \(\displaystyle\frac{dy}{dx}=x+y\) and \(y(0)=1\).
2) \(\displaystyle\frac{dy}{dx}=x^2+y^2-1\) and \(y(0)=0\).
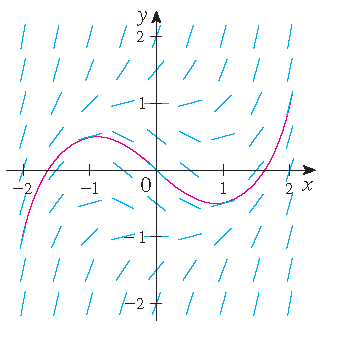
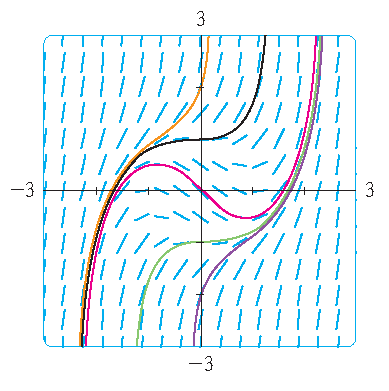
3) \(\displaystyle\frac{dy}{dx}=x^2+y^2-1\) and \(y(0)=k\) with \(k\in\{-2,-1,0,1,2\}\).
Last modified on March 8, 2021
 Teaching
Teaching

