Analyse – Eerste orde differentiaalvergelijkingen
Definitie Een differentiaalvergelijking is een vergelijking in een onbekende functie en één of meer van haar afgeleiden. De orde van de hoogste afgeleide die voorkomt heet de orde van de differentiaalvergelijking.
Voorlopig bekijken we alleen eerste orde differentiaalvergelijkingen van de vorm \(\displaystyle\frac{dy}{dx}=F(x,y)\) met \(y=y(x)\).
Populatiegroei
Eén model voor de groei van een populatie is gebaseerd op de aanname dat de populatie groeit met een snelheid evenredig met de grootte van de populatie.
Dat is een redelijke aanname voor een populatie bacterieën of dieren onder ideale omstandigheden (de leefomgeving is onbeperkt, er is voldoene voedsel, er zijn geen roofdieren en immuniteit voor ziektes).
Als \(P(t)\) het aantal individuën in een populatie aangeeft op tijdstip \(t\), dan is: \(\displaystyle\frac{dP}{dt}=kP\), waarbij \(k\) de groeisnelheid is. Dit heet exponentiële groei, omdat de algemene oplossing \(P(t)=Ce^{kt}\) is met \(C\in\mathbb{R}\).
Een meer realistisch model is \(\displaystyle\frac{dP}{dt}=kP\left(1-\frac{P}{M}\right)\). Dit heet een logistische differentiaalvergelijking.
Deze differentiaalvergelijking is in 1838 door de Belgische wiskundige Pierre-François Verhulst geïntroduceerd als een model voor de groei van de wereldbevolking.
Dit meer realistische model houdt rekening met het feit dat een zeker leefgebied beperkende factoren heeft. Veel populaties beginnen op een exponentiële manier te groeien, maar dan wordt de groei van de populatie afgevlakt als deze een bepaalde limietwaarde \(M\) benadert (of als deze daalt naar \(M\) als deze waarde \(M\) ooit wordt overschreden).
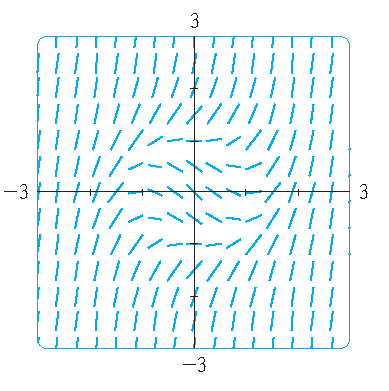
In plaats van differentiaalvergelijkingen van de vorm \(\displaystyle\frac{dy}{dx}=F(x,y)\) op te lossen is het ook mogelijk om te kijken naar richtingsvelden.
Voorbeelden:
1) \(\displaystyle\frac{dy}{dx}=x+y\) en \(y(0)=1\).
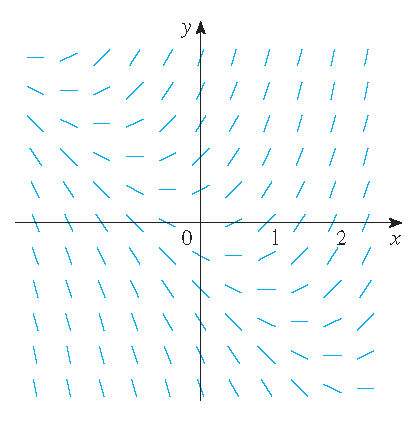
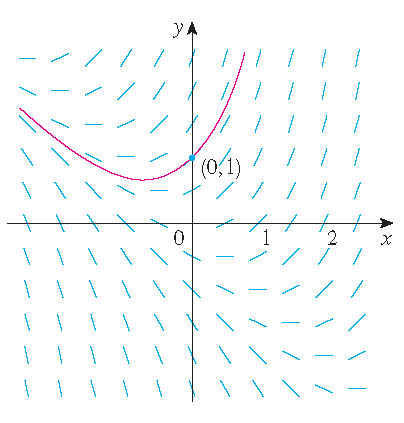
2) \(\displaystyle\frac{dy}{dx}=x^2+y^2-1\) en \(y(0)=0\).
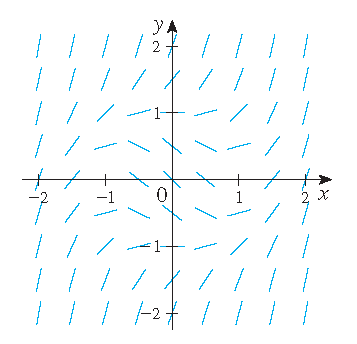
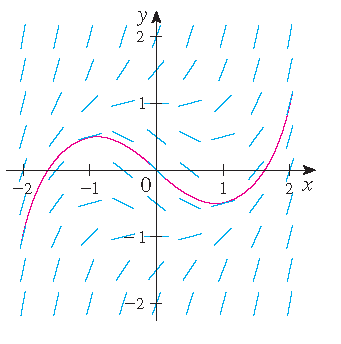
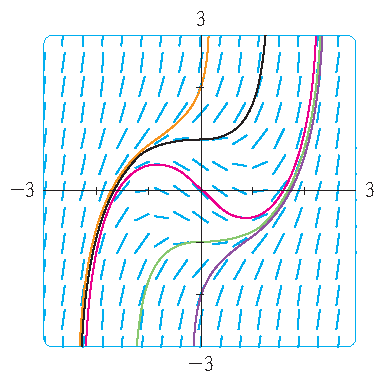
3) \(\displaystyle\frac{dy}{dx}=x^2+y^2-1\) en \(y(0)=k\) met \(k\in\{-2,-1,0,1,2\}\).
Laatst gewijzigd op 8 maart 2021
 Onderwijs
Onderwijs

