Analyse – Integreren – Toepassingen

De normale verdeling

In de waarschijnlijkheidsrekening en de statistiek speelt de normale verdeling een belangrijke rol. Deze is gebaseerd op de grafiek van de functie \(e^{-x^2}\):

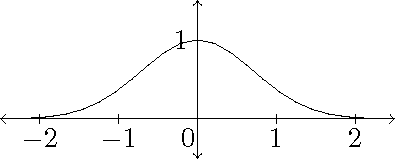
Deze grafiek wordt soms een Gaussische kromme of een klokkromme genoemd. Vanwege de symmetrie geldt dat \(\displaystyle\int_{-\infty}^{\infty}e^{-x^2}\,dx=2\int_0^{\infty}e^{-x^2}\,dx\).

In Stewart §7.8, Voorbeeld 9 wordt aangetoond dat deze integraal convergent is:

\[\int_0^{\infty}e^{-x^2}\,dx=\int_0^1e^{-x^2}\,dx+\int_1^{\infty}e^{-x^2}\,dx.\]

De eerste integraal aan de rechterkant is gewoon een eindige integraal. Voor de tweede integraal gebruiken we dat voor \(x\geq1\) geldt dat \(x^2\geq x\), dus \(−x^2\leq-x\) en dus \(e^{-x^2}\leq e^{-x}\). Nu geldt:

\[\int_1^{\infty}e^{-x}\,dx=\lim\limits_{t\to\infty}\int_1^te^{-x}\,dx=\lim\limits_{t\to\infty}\left(e^{-1}-e^{-t}\right)=e^{-1}.\]

Dit toont aan dat de tweede integraal convergeert.

Later zullen we bewijzen dat \(\displaystyle\int_0^{\infty}e^{-x^2}\,dx=\tfrac{1}{2}\sqrt{\pi}\), waaruit volgt dat \(\displaystyle\int_{-\infty}^{\infty}e^{-x^2}\,dx=\sqrt{\pi}\). Dit wordt wel de Gaussische integraal genoemd.

Uiteraard is het in de waarschijnlijkheidsrekening en de statistiek essentieel dat \(\displaystyle\frac{1}{\sqrt{\pi}}\int_{-\infty}^{\infty}e^{-x^2}\,dx=1\).

De Cauchy verdeling

De Cauchy verdeling is een andere kansverdeling die gebaseerd is op de grafiek van de functie \(\displaystyle\frac{1}{1+x^2}\):

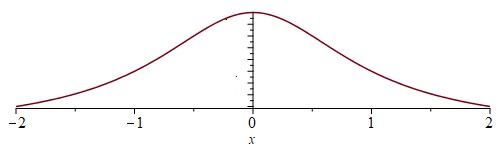
In Stewart §7.8, Voorbeeld 3 wordt deze integraal berekend:

\[\int_{-\infty}^{\infty}\frac{1}{1+x^2}\,dx=\int_{-\infty}^0\frac{1}{1+x^2}\,dx+\int_0^{\infty}\frac{1}{1+x^2}\,dx.\]

Nu geldt:

\[\int_0^{\infty}\frac{1}{1+x^2}\,dx=\arctan(x)\bigg|_0^{\infty}=\frac{1}{2}\pi-0=\frac{1}{2}\pi\quad\text{en}\quad \int_{-\infty}^0\frac{1}{1+x^2}\,dx=\arctan(x)\bigg|_{-\infty}^0=0-\left(-\frac{1}{2}\pi\right)=\frac{1}{2}\pi.\]

Hieruit volgt dat

\[\int_{-\infty}^{\infty}\frac{1}{1+x^2}\,dx=\frac{1}{2}\pi+\frac{1}{2}\pi=\pi.\]

Hier geldt dus dat \(\displaystyle\frac{1}{\pi}\int_{-\infty}^{\infty}\frac{1}{1+x^2}\,dx=1\).

De gammafunctie

Voor \(x>0\) wordt de gammafunctie gedefinieerd als \(\displaystyle\Gamma(x)=\int_0^{\infty}t^{x-1}e^{-t}\,dt\). Men kan aantonen dat deze integraal convergeert voor \(x>0\).

Merk op dat \(\Gamma(1)=\displaystyle\int_0^{\infty}e^{-t}\,dt=-e^{-t}\bigg|_0^{\infty}=1\).

Met behulp van partiële integratie vinden we voor \(x>0\)

\[\Gamma(x+1)=\int_0^{\infty}t^xe^{-t}\,dt=-\int_0^{\infty}t^x\,de^{-t}=-t^xe^{-t}\bigg|_0^{\infty}+\int_0^{\infty}e^{-t}\,dt^x =0+x\int_0^{\infty}t^{x-1}e^{-t}\,dt=x\Gamma(x).\]

Merk op dat hieruit volgt dat\({}^{(*)}\) \(\Gamma(n+1)=n!\) voor \(n=0,1,2,\ldots\). Dus, de gammafunctie kan worden gezien als een generalisatie van de faculteit.

Verder volgt met de substitutie \(t=x^2\) dat

\[\Gamma(\tfrac{1}{2})=\int_0^{\infty}t^{-\frac{1}{2}}e^{-t}\,dt=\int_0^{\infty}x^{-1}e^{-x^2}\cdot2x\,dx=2\int_0^{\infty}e^{-x^2}\,dx.\]

Later zullen we bewijzen dat \(\displaystyle\int_0^{\infty}e^{-x^2}\,dx=\tfrac{1}{2}\sqrt{\pi}\). Hieruit volgt dat \(\Gamma(\frac{1}{2})=\sqrt{\pi}\).

---

\({}^{(*)}\) De faculteit wordt gedefinieerd door \(n!=1\cdot2\cdot3\cdots n\) voor \(n=1,2,3,\ldots\). Als we afspreken dat \(0!=1\), dan geldt:

\[0!=1\quad\text{en}\quad n!=n(n-1)!,\quad n=1,2,3,\ldots.\]

---

Laatst gewijzigd op 8 maart 2021