Analyse – Integreren

Voor een positieve functie \(f\) gedefinieerd op een interval \([a,b]\) is de integraal

\[\int_a^bf(x)\,dx\]

de oppervlakte tussen de grafiek van \(f\) en de \(x\)-as tussen \(a\) en \(b\):

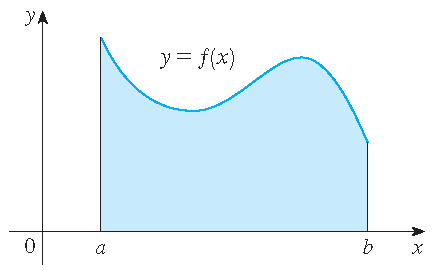
We beginnen met een benadering: verdeel het interval \([a,b]\) in deelintervallen en beschouw de som van de oppervlaktes van de aangegeven rechthoeken.

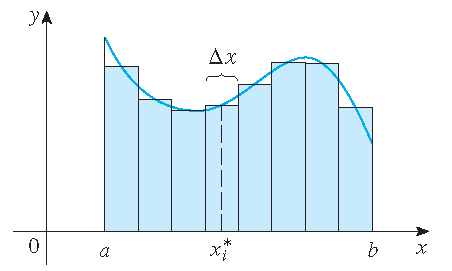
Verdeel het interval \([a,b]\) in \(n\) deelintervallen met gelijke breedte \((b-a)/n\):

\[a=x_0 < x_1 < x_2 < \ldots < x_{n-1} < x_n=b.\]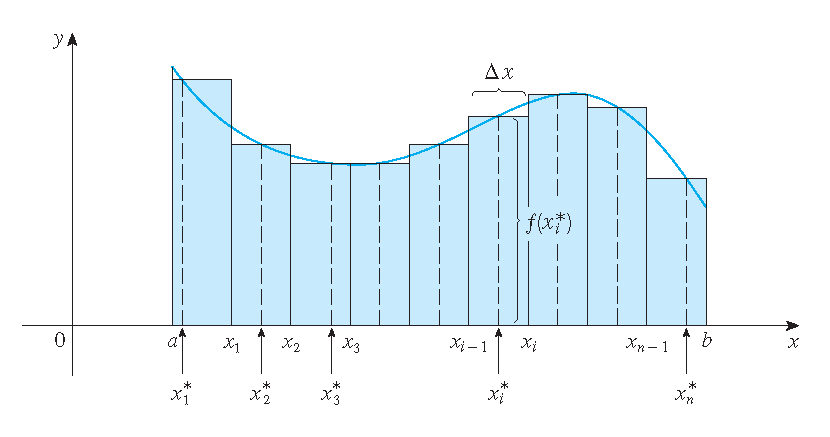

Kies een strooipunt \(x_i^*\) in elk deelinterval \([x_{i-1},x_i]\), dan volgt:

\[\int_a^bf(x)\,dx=\lim_{n\to\infty}\,\sum_{i=1}^nf(x_i^*)\Delta x\quad\text{met}\quad\Delta x=x_i-x_{i-1}=\frac{b-a}{n}.\]

De som \(\displaystyle\sum_{i=1}^nf(x_i^*)(x_i-x_{i-1})\) heet een Riemann som.

Opmerkingen:

1. Het integraalteken \(\displaystyle\int\) werd geïntroduceerd door Leibniz en heeft de vorm van een (lange) uitgerekte \(S\) dat aangeeft dat het de limiet is van (Riemann) sommen.


2. Onze definitie van de integraal van een positieve functie geldt als de functie continu is op het interval \([a,b]\), maar kan eenvoudig worden uitgebreid tot stuksgewijs continue functies.


3. We hebben ervoor gekozen om het interval \([a,b]\) in \(n\) deelintervallen van gelijke breedte \(\Delta x=(b-a)/n\) te verdelen, maar dat is niet echt nodig.





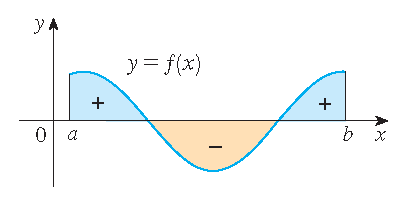
4. Voor negatieve functies wordt de integraal gedefinieerd als minus de oppervlakte tussen de grafiek van \(f\) en de \(x\)-as. Als \(f\) zowel positieve als negatieve waarden aanneemt dan is de integraal gelijk aan de totale oppervlakte boven de \(x\)-as minus de totale oppervlakte onder de \(x\)-as.


5. Een functie waarvoor de limiet van de Riemann sommen bestaat heet integreerbaar; elke stuksgewijs continue functie op een interval \([a,b]\) is integreerbaar (de integraal ervan bestaat).

Hoofdstelling van de integraalrekening (1): Als \(f\) continu is op \([a,b]\), dan is de functie \(F\) gedefinieerd door

\[F(x)=\int_a^xf(t)\,dt,\quad a\leq x\leq b\]

continu op \([a,b]\) en differentieerbaar op \((a,b)\), en \(F'(x)=f(x)\).

Definitie: Elke functie \(F\) met de eigenschap dat \(F'(x)=f(x)\) voor alle \(x\) heet een primitieve van \(f\).

Hoofdstelling van de integraalrekening (2): Als \(f\) continu is op \([a,b]\), dan is

\[\int_a^bf(x)\,dx=F(b)-F(a),\]

waarbij \(F\) een willekeurige primitieve van \(f\) is, dat wil zeggen: \(F'=f\).

---

Laatst gewijzigd op 8 maart 2021