Calculus

Calculus – Integration

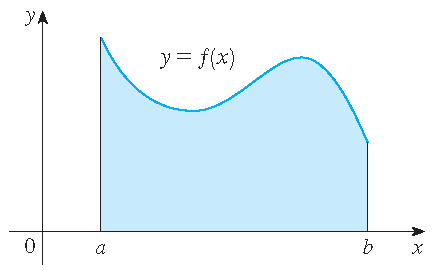
For a positive function \(f\) defined on an interval \([a,b]\) the integral

\[\int_a^bf(x)\,dx\]

is the area between the graph of \(f\) and the \(x\)-axis between \(a\) and \(b\):

We start with an approximation: divide the interval \([a,b]\) into subintervals and consider the sum of the areas of the indicated rectangles.

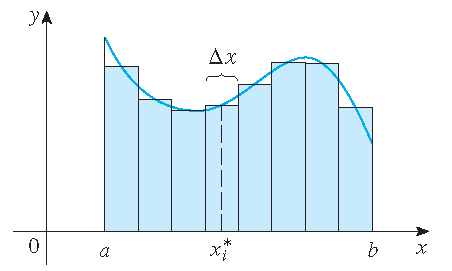
Divide the interval \([a,b]\) into \(n\) subintervals of equal width \((b-a)/n\):

\[a=x_0 < x_1 < x_2 < \ldots < x_{n-1} < x_n=b.\]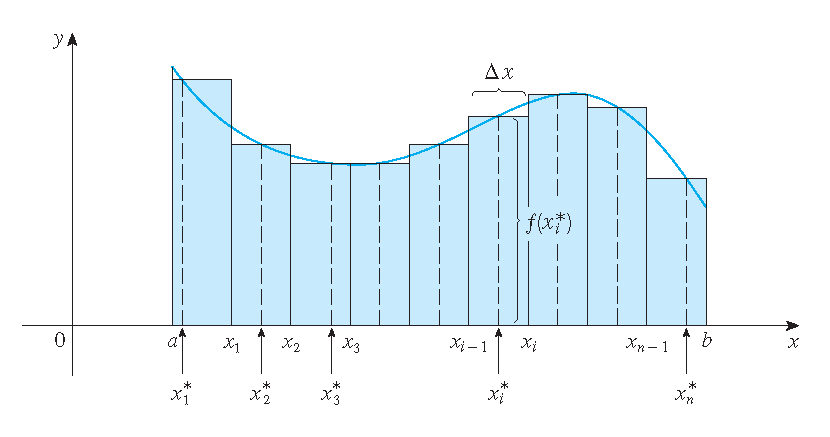

Choose a sample point \(x_i^*\) in each subinterval \([x_{i-1},x_i]\), then:

\[\int_a^bf(x)\,dx=\lim_{n\to\infty}\,\sum_{i=1}^nf(x_i^*)\Delta x\quad\text{with}\quad\Delta x=x_i-x_{i-1}=\frac{b-a}{n}.\]

The sum \(\displaystyle\sum_{i=1}^nf(x_i^*)(x_i-x_{i-1})\) is called a Riemann sum.

Remarks:

The integral sign \(\displaystyle\int\) was introduced by Leibniz and has the form of an elongated (stretched) \(S\) which indicates the limit of (Riemann) sums.

Our definition of the integral of a positive function holds when the function is continuous on the interval \([a,b]\), but can easily be extended to piecewise continuous functions.

We have chosen to divide the interval \([a,b]\) into \(n\) subintervals of equal width \(\Delta x=(b-a)/n\) which is not really necessary.

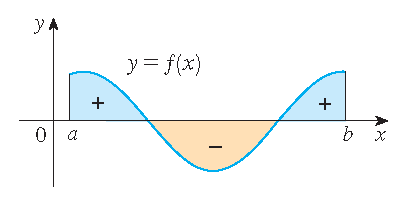
For negative functions the integral is defined as minus the area between the graph of \(f\) and the \(x\)-axis. If \(f\) takes on both positive and negative values the integral equals the total area above the \(x\)-axis minus the total area below the \(x\)-axis.

A function for which the limit of the Riemann sums exists is called integrable; every piecewise continuous function on an interval \([a,b]\) is integrable (its integral exists).