Calculus – Integration – Improper integrals

Improper integrals of type 1: an infinite interval of integration.

Definition:

• If \(\displaystyle\int_a^bf(x)\,dx\) exists for every \(b\geq a\), then \(\displaystyle\int_a^{\infty}f(x)\,dx=\lim\limits_{b\to\infty}\int_a^bf(x)\,dx\) if this limit exists.


• If \(\displaystyle\int_a^bf(x)\,dx\) exists for every \(a\leq b\), then \(\displaystyle\int_{-\infty}^bf(x)\,dx=\lim\limits_{a\to-\infty}\int_a^bf(x)\,dx\) if this limit exists.

The improper integrals \(\displaystyle\int_a^{\infty}f(x)\,dx\) and \(\displaystyle\int_{-\infty}^bf(x)\,dx\) are called convergent if the corresponding limit exists and divergent if the limit does not exist.

• If both \(\displaystyle\int_c^{\infty}f(x)\,dx\) and \(\displaystyle\int_{-\infty}^cf(x)\,dx\) are convergent, then \(\displaystyle\int_{-\infty}^{\infty}f(x)\,dx=\int_{-\infty}^cf(x)\,dx+\int_c^{\infty}f(x)\,dx\).

Improper integrals of type 2: a discontinuous integrand.

Definition:

• If \(f\) is continuous on \([a,b)\) and discontinuous at \(b\), then \(\displaystyle\int_a^bf(x)\,dx=\lim\limits_{t\uparrow b}\int_a^tf(x)\,dx\) if this limit exists.


• If \(f\) is continuous on \((a,b]\) and discontinuous at \(a\), then \(\displaystyle\int_a^bf(x)\,dx=\lim\limits_{t\downarrow a}\int_t^bf(x)\,dx\) if this limit exists.

The improper integral \(\displaystyle\int_a^bf(x)\,dx\) is called convergent if the corresponding limit exists and divergent if the limit does not exist.

• If \(f\) has a discontinuity at \(c\) where \(a < c < b\) and both \(\displaystyle\int_a^cf(x)\,dx\) and \(\displaystyle\int_c^bf(x)\,dx\) are convergent, then \(\displaystyle\int_a^bf(x)\,dx=\int_a^cf(x)\,dx+\int_c^bf(x)\,dx\).

A comparison test for improper integrals

Theorem: Suppose that \(f\) and \(g\) are continuous functions with 0\(\leq g(x)\leq f(x)\) for \(x\geq a\), then:

1. \(\displaystyle\int_a^{\infty}f(x)\,dx\) convergent \({}\;\Longrightarrow\;\displaystyle\int_a^{\infty}g(x)\,dx\) convergent,


2. \(\displaystyle\int_a^{\infty}g(x)\,dx\) divergent \({}\;\Longrightarrow\;\displaystyle\int_a^{\infty}f(x)\,dx\) divergent.

For improper integrals of type 2 we have a similar theorem.

Gabriel's horn or Torricelli's trumpet

Stewart §7.8, Example 1
Since we have \(\displaystyle\int_1^{\infty}\frac{1}{x}\,dx=\lim\limits_{b\to\infty}\int_1^b\frac{1}{x}\,dx=\lim\limits_{b\to\infty}\ln(b)=\infty\), we conclude that the area of the region \(\mathcal{R}=\{(x,y)\,|\,x\geq1,\;0\leq y\leq\frac{1}{x}\}\) is infinite:

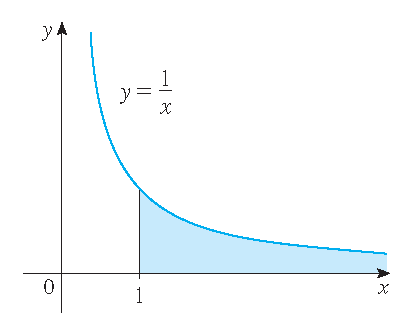
Stewart §7.8, Exercise 63
Show by rotating \(\mathcal{R}\) about the \(x\)-axis we obtain a solid with finite volume.

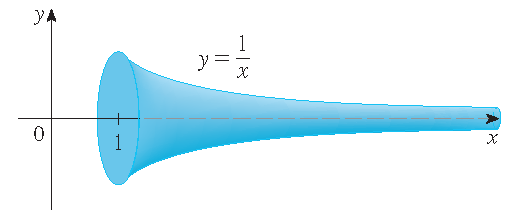
The surface shown in the picture is known as Gabriel's horn or Torricelli's trumpet.

Solution:
Using that the area of a circle with radius \(r\) equals \(\pi r^2\), we obtain that the volume equals: \(V=\pi\displaystyle\int_1^{\infty}\frac{1}{x^2}\,dx=\pi\bigg[-\frac{1}{x}\bigg]_1^{\infty}=\pi\).

Stewart §8.2, Exercise 27
Show that the surface area is infinite.

Solution:
In Stewart §8.2 it is explained that the surface area of the surface obtained by rotating the curve \(y=f(x)\) with \(a\leq x\leq b\) about the \(x\)-axis is given by

\[A=2\pi\displaystyle\int_a^bf(x)\sqrt{1+\{f'(x)\}^2}\,dx.\]

So for \(f(x)=\displaystyle\frac{1}{x}\) with \(x\geq1\) we obtain

\[A=2\pi\int_1^{\infty}\frac{1}{x}\sqrt{1+\left(-\frac{1}{x^2}\right)^2}\,dx > 2\pi\int_1^{\infty}\frac{1}{x}\,dx=\infty.\]

---

Last modified on March 8, 2021