Analyse – Integreren – Oneigenlijke integralen

Oneigenlijke integralen van type 1: een oneindig integratie-interval.

Definitie:

• Als \(\displaystyle\int_a^bf(x)\,dx\) bestaat voor iedere \(b\geq a\), dan is \(\displaystyle\int_a^{\infty}f(x)\,dx=\lim\limits_{b\to\infty}\int_a^bf(x)\,dx\) als deze limiet bestaat.


• Als \(\displaystyle\int_a^bf(x)\,dx\) bestaat voor iedere \(a\leq b\), dan is \(\displaystyle\int_{-\infty}^bf(x)\,dx=\lim\limits_{a\to-\infty}\int_a^bf(x)\,dx\) als deze limiet bestaat.

De oneigenlijke integralen \(\displaystyle\int_a^{\infty}f(x)\,dx\) en \(\displaystyle\int_{-\infty}^bf(x)\,dx\) heten convergent als de corresponderende limiet bestaat en divergent als de limiet niet bestaat.

• Als zowel \(\displaystyle\int_c^{\infty}f(x)\,dx\) als \(\displaystyle\int_{-\infty}^cf(x)\,dx\) convergent zijn, dan is \(\displaystyle\int_{-\infty}^{\infty}f(x)\,dx=\int_{-\infty}^cf(x)\,dx+\int_c^{\infty}f(x)\,dx\).

Oneigenlijke integralen van type 2: een discontinue integrand.

Definitie:

• Als \(f\) continu is op \([a,b)\) en discontinu in \(b\), dan is \(\displaystyle\int_a^bf(x)\,dx=\lim\limits_{t\uparrow b}\int_a^tf(x)\,dx\) als deze limiet bestaat.


• Als \(f\) continu is op \((a,b]\) en discontinu in \(a\), dan is \(\displaystyle\int_a^bf(x)\,dx=\lim\limits_{t\downarrow a}\int_t^bf(x)\,dx\) als deze limiet bestaat.

De oneigenlijke integraal \(\displaystyle\int_a^bf(x)\,dx\) heet convergent als de corresponderende limiet bestaat en divergent als de limiet niet bestaat.

• Als \(f\) een discontinuïteit heeft in \(c\) waarbij \(a < c < b\) en zowel \(\displaystyle\int_a^cf(x)\,dx\) als \(\displaystyle\int_c^bf(x)\,dx\) zijn convergent, dan is \(\displaystyle\int_a^bf(x)\,dx=\int_a^cf(x)\,dx+\int_c^bf(x)\,dx\).

Een vergelijkingstest voor oneigenlijke integralen

Stelling: Neem aan dat \(f\) en \(g\) continue functies zijn met 0\(\leq g(x)\leq f(x)\) voor \(x\geq a\), dan geldt:

1. \(\displaystyle\int_a^{\infty}f(x)\,dx\) convergent \({}\;\Longrightarrow\;\displaystyle\int_a^{\infty}g(x)\,dx\) convergent,


2. \(\displaystyle\int_a^{\infty}g(x)\,dx\) divergent \({}\;\Longrightarrow\;\displaystyle\int_a^{\infty}f(x)\,dx\) divergent.

Voor oneigenlijke integralen van type 2 hebben we een soortgelijke stelling.

Gabriel's hoorn of Torricelli's trompet

Stewart §7.8, Voorbeeld 1
Omdat geldt dat \(\displaystyle\int_1^{\infty}\frac{1}{x}\,dx=\lim\limits_{b\to\infty}\int_1^b\frac{1}{x}\,dx=\lim\limits_{b\to\infty}\ln(b)=\infty\), concluderen we dat de oppervlakte van het gebied \(\mathcal{R}=\{(x,y)\,|\,x\geq1,\;0\leq y\leq\frac{1}{x}\}\) oneindig is:

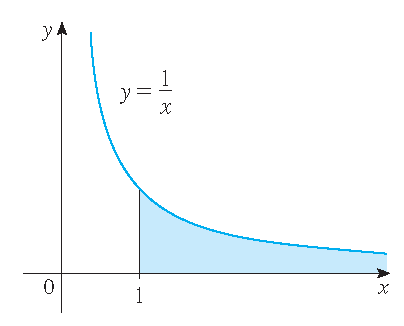
Stewart §7.8, Opgave 63
Toon aan door \(\mathcal{R}\) te roteren rond de \(x\)-as dat we dan een lichaam met een eindig volume krijgen.

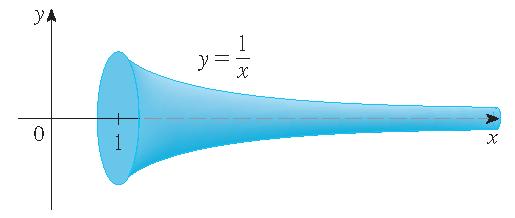
Het oppervlak in het plaatje staat bekend als Gabriel's hoorn of Torricelli's trompet.

Oplossing:
Omdat de oppervlakte van een cirkel met straal \(r\) gelijk is aan \(\pi r^2\), volgt dat het volume gelijk is aan: \(V=\pi\displaystyle\int_1^{\infty}\frac{1}{x^2}\,dx=\pi\bigg[-\frac{1}{x}\bigg]_1^{\infty}=\pi\).

Stewart §8.2, Opgave 27
Toon aan dat de oppervlakte van het oppervlak oneindig is.

Oplossing:
In Stewart §8.2 wordt uitgelegd dat de oppervlakte van het omwentelingsoppervlak dat wordt verkregen door de kromme \(y=f(x)\) met \(a\leq x\leq b\) te wentelen om de \(x\)-as wordt gegeven door

\[A=2\pi\displaystyle\int_a^bf(x)\sqrt{1+\{f'(x)\}^2}\,dx.\]

Dus voor \(f(x)=\displaystyle\frac{1}{x}\) met \(x\geq1\) vinden we

\[A=2\pi\int_1^{\infty}\frac{1}{x}\sqrt{1+\left(-\frac{1}{x^2}\right)^2}\,dx > 2\pi\int_1^{\infty}\frac{1}{x}\,dx=\infty.\]

---

Laatst gewijzigd op 8 maart 2021