Calculus – Trigonometry – The Pythagorean theorem

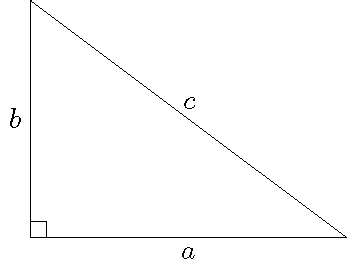
Theorem: In a right-angled triangle with rectangular sides \(a\) and \(b\) and hypotenuse \(c\) we have: \(a^2+b^2=c^2\).

Proof: An elegant proof of the Pythagorean theorem is based on the following picture:

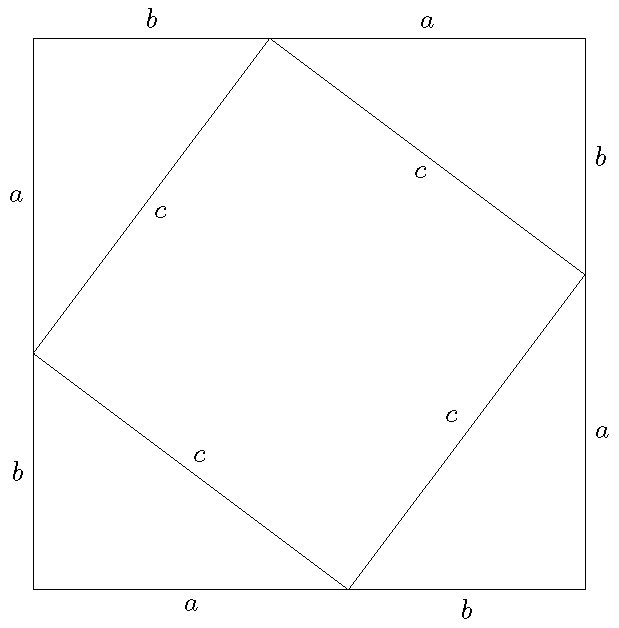
The area of the large square is \((a+b)^2\) and that of the small square is \(c^2\). The area of one of the four triangles is \(\frac{1}{2}ab\). So we have:

\[(a+b)^2=c^2+4\cdot\tfrac{1}{2}ab\quad\Longleftrightarrow\quad a^2+2ab+b^2=c^2+2ab\quad\Longleftrightarrow\quad a^2+b^2=c^2.\]

The law of cosines is a generalization of the Pythagorean theorem:

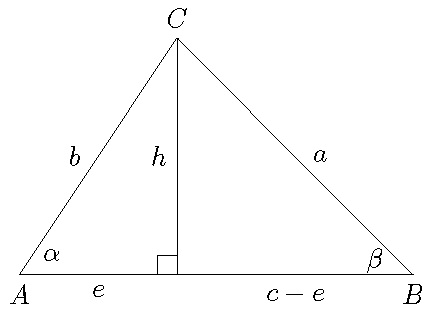
Theorem: In an arbitrary triangle we have: \(a^2=b^2+c^2-2bc\cos(\alpha)\).

Proof: In the figure above we have according to the Pythagorean theorem: \(h^2=b^2-e^2\) and \(h^2=a^2-(c-e)^2\). Hence: \[b^2-e^2=a^2-c^2+2ce-e^2\quad\Longleftrightarrow\quad b^2=a^2-c^2+2ce.\]

Now we have: \(\cos(\alpha)=\dfrac{e}{b}\), which implies that \(e=b\cos(\alpha)\). So:

\[a^2=b^2+c^2-2bc\cos(\alpha).\]

Further we have the law of sines:

Theorem: In an arbitrary triangle we have: \(\dfrac{a}{\sin(\alpha)}=\dfrac{b}{\sin(\beta)}\).

Proof: In the figure above we have: \(\sin(\alpha)=\dfrac{h}{b}\) and \(\sin(\beta)=\dfrac{h}{a}\). Hence: \(b\sin(\alpha)=h=a\sin(\beta)\) or equivalently \(\dfrac{a}{\sin(\alpha)}=\dfrac{b}{\sin(\beta)}\).

The last result can be extended with:

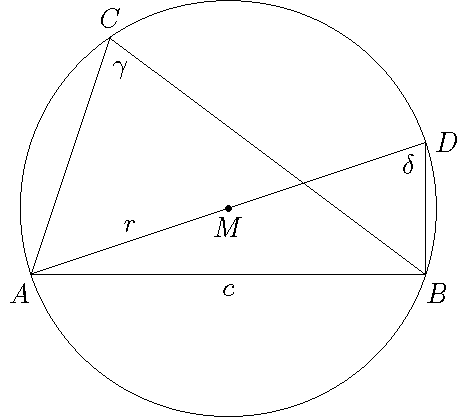
Theorem: \(\dfrac{c}{\sin(\gamma)}=2r\) with \(r\) the radius of the circumscribed circle of the triangle.

Proof: Consider the line segment \(AD\) through the center \(M\) of the circumscribed circle of the triangle. According to Thales's theorem the triangle \(ABD\) then is a right-angled triangle. Since \(C\) and \(D\) are two points on the same circle, which are connected to the same chord \(AB\), we have: \(\gamma=\delta\). Then we have:

\[\sin(\gamma)=\sin(\delta)=\frac{c}{2r}\quad\Longleftrightarrow\quad\frac{c}{\sin(\gamma)}=2r.\]

---

Last modified on October 4, 2025