Calculus – Trigonometry – Triangle identities

We consider an arbitrary triangle \(ABC\) with vertices \(A\), \(B\) and \(C\), sides \(a\), \(b\) and \(c\) and angles \(\alpha\), \(\beta\) and \(\gamma\), where \(\alpha+\beta+\gamma=\pi\).

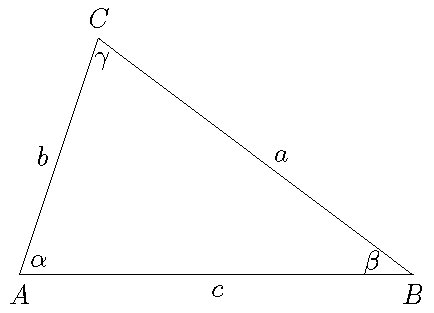
Then we have the law of cosines :

\[a^2=b^2+c^2-2bc\cos(\alpha),\quad b^2=a^2+c^2-2ac\cos(\beta)\quad\text{and}\quad c^2=a^2+b^2-2ab\cos(\gamma).\]

Further we have the law of sines :

\[\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}=d,\]

where \(d\) denotes the diameter of the circumscribed circle.

1)

\[a\sin(\beta-\gamma)+b\sin(\gamma-\alpha)+c\sin(\alpha-\beta)=0.\]

Proof:

\begin{align*} a\sin(\beta-\gamma)+b\sin(\gamma-\alpha)+c\sin(\alpha-\beta) &=d\sin(\alpha)\sin(\beta-\gamma)+d\sin(\beta)\sin(\gamma-\alpha)+d\sin(\gamma)\sin(\alpha-\beta)\\ &=d\sin(\pi-\alpha)\sin(\beta-\gamma)+d\sin(\pi-\beta)\sin(\gamma-\alpha)+d\sin(\pi-\gamma)\sin(\alpha-\beta)\\ &=d\sin(\beta+\gamma)\sin(\beta-\gamma)+d\sin(\gamma+\alpha)\sin(\gamma-\alpha)+d\sin(\alpha+\beta)\sin(\alpha-\beta)\\ &=d\left(\sin^2(\beta)-\sin^2(\gamma)+\sin^2(\gamma)-\sin^2(\alpha)+\sin^2(\alpha)-\sin^2(\beta)\right)=0. \end{align*}

2)

\[a\cos(\alpha)+b\cos(\beta)+c\cos(\gamma)=2R\quad\text{with}\quad R\in\{a\sin(\beta)\sin(\gamma),b\sin(\alpha)\sin(\gamma),c\sin(\alpha)\sin(\beta)\}.\]

Proof:

\begin{align*} a\cos(\alpha)+b\cos(\beta)+c\cos(\gamma) &=d\sin(\alpha)\cos(\alpha)+d\sin(\beta)\cos(\beta)+d\sin(\gamma)\cos(\gamma) =\frac{1}{2}d\left(\sin(2\alpha)+\sin(2\beta)+2\sin(\gamma)\cos(\gamma)\right)\\ &=d\left(\sin(\alpha+\beta)\cos(\alpha-\beta)+\sin(\gamma)\cos(\gamma)\right) =d\left(\sin(\gamma)\cos(\alpha-\beta)-\sin(\gamma)\cos(\alpha+\beta)\right)\\ &=d\sin(\gamma)\left(\cos(\alpha-\beta)-\cos(\alpha+\beta)\right)=2d\sin(\gamma)\sin(\alpha)\sin(\beta)=2R, \end{align*}

with \(R=d\sin(\alpha)\sin(\beta)\sin(\gamma)=a\sin(\beta)\sin(\gamma)=b\sin(\alpha)\sin(\gamma)=c\sin(\alpha)\sin(\beta)\).

3)

\[\sin^2(\alpha)+\sin^2(\beta)+\sin^2(\gamma)=2+2\cos(\alpha)\cos(\beta)\cos(\gamma).\]

Proof:

\begin{align*} \sin^2(\alpha)+\sin^2(\beta)+\sin^2(\gamma)&=1-\cos^2(\alpha)+1-\cos^2(\beta)+\sin^2(\gamma) =2-\left(\cos^2(\alpha)-\sin^2(\gamma)\right)-\cos^2(\beta)\\ &=2-\cos(\alpha+\gamma)\cos(\alpha-\gamma)-\cos^2(\beta)=2+\cos(\beta)\cos(\alpha-\gamma)-\cos^2(\beta)\\ &=2+\cos(\beta)\left(\cos(\alpha-\gamma)-\cos(\beta)\right)=2+\cos(\beta)\left(\cos(\alpha-\gamma)+\cos(\alpha+\gamma)\right)\\ &=2+2\cos(\alpha)\cos(\beta)\cos(\gamma). \end{align*}

Note that this implies that a triangle with angles \(\alpha\), \(\beta\) and \(\gamma\) is a right-angled triangle if and only if \(\sin^2(\alpha)+\sin^2(\beta)+\sin^2(\gamma)=2\) since then \(\cos(\alpha)=0\), \(\cos(\beta)=0\) or \(\cos(\gamma)=0\).

4)

\[\cos^2(\alpha)+\cos^2(\beta)+\cos^2(\gamma)=1-2\cos(\alpha)\cos(\beta)\cos(\gamma).\]

Proof:

\begin{align*} \cos^2(\alpha)+\cos^2(\beta)+\cos^2(\gamma)&=1-\sin^2(\alpha)+\cos^2(\beta)+\cos^2(\gamma) =1+\left(\cos^2(\beta)-\sin^2(\alpha)\right)+\cos^2(\gamma)\\ &=1+\cos(\beta+\alpha)\cos(\beta-\alpha)+\cos^2(\gamma)=1-\cos(\gamma)\cos(\beta-\alpha)+\cos^2(\gamma)\\ &=1-\cos(\gamma)\left(\cos(\beta-\alpha)-\cos(\gamma)\right)=1-\cos(\gamma)\left(\cos(\beta-\alpha)+\cos(\beta+\alpha)\right)\\ &=1-2\cos(\alpha)\cos(\beta)\cos(\gamma). \end{align*}

Note that this implies that a triangle with angles \(\alpha\), \(\beta\) and \(\gamma\) is a right-angled triangle if and only if \(\cos^2(\alpha)+\cos^2(\beta)+\cos^2(\gamma)=1\) since then \(\cos(\alpha)=0\), \(\cos(\beta)=0\) or \(\cos(\gamma)=0\).

5)

\[\sin^2(\alpha)+\sin^2(\beta)-\sin^2(\gamma)=2\sin(\alpha)\sin(\beta)\cos(\gamma).\]

Proof:

\begin{align*} \sin^2(\alpha)+\sin^2(\beta)-\sin^2(\gamma)&=\sin^2(\alpha)+\sin(\beta+\gamma)\sin(\beta-\gamma) =\sin^2(\alpha)+\sin(\alpha)\sin(\beta-\gamma)\\ &=\sin(\alpha)\left(\sin(\alpha)+\sin(\beta-\gamma)\right)=\sin(\alpha)\left(\sin(\beta+\gamma)+\sin(\beta-\gamma)\right)\\ &=2\sin(\alpha)\sin(\beta)\cos(\gamma). \end{align*}

6)

\[\cos^2(\alpha)+\cos^2(\beta)-\cos^2(\gamma)=1-2\sin(\alpha)\sin(\beta)\cos(\gamma).\]

Proof:

\begin{align*} \cos^2(\alpha)+\cos^2(\beta)-\cos^2(\gamma)&=\cos^2(\alpha)+\sin(\beta+\gamma)\sin(\beta-\gamma) =1-\sin^2(\alpha)+\sin(\alpha)\sin(\beta-\gamma)\\ &=1-\sin(\alpha)\left(\sin(\alpha)+\sin(\beta-\gamma)\right)=1-\sin(\alpha)\left(\sin(\beta+\gamma)+\sin(\beta-\gamma)\right)\\ &=1-2\sin(\alpha)\sin(\beta)\cos(\gamma). \end{align*}

7)

\[\sin(2\alpha)+\sin(2\beta)+\sin(2\gamma)=4\sin(\alpha)\sin(\beta)\sin(\gamma).\]

Proof:

\begin{align*} \sin(2\alpha)+\sin(2\beta)+\sin(2\gamma)&=2\sin(\alpha+\beta)\cos(\alpha-\beta)+\sin(2\gamma) =2\sin(\gamma)\cos(\alpha-\beta)+2\sin(\gamma)\cos(\gamma)\\ &=2\sin(\gamma)\left(\cos(\alpha-\beta)+\cos(\gamma)\right) =2\sin(\gamma)\left(\cos(\alpha-\beta)-\cos(\alpha+\beta)\right)=4\sin(\alpha)\sin(\beta)\sin(\gamma). \end{align*}

8)

\[\sin(2\alpha)+\sin(2\beta)-\sin(2\gamma)=4\cos(\alpha)\cos(\beta)\sin(\gamma).\]

Proof:

\begin{align*} \sin(2\alpha)+\sin(2\beta)-\sin(2\gamma)&=2\sin(\alpha+\beta)\cos(\alpha-\beta)-\sin(2\gamma) =2\sin(\gamma)\cos(\alpha-\beta)-2\sin(\gamma)\cos(\gamma)\\ &=2\sin(\gamma)\left(\cos(\alpha-\beta)-\cos(\gamma)\right) =2\sin(\gamma)\left(\cos(\alpha-\beta)+\cos(\alpha+\beta)\right)=4\cos(\alpha)\cos(\beta)\sin(\gamma). \end{align*}

9)

\[a^3\cos(\beta)\cos(\gamma)+b^3\cos(\alpha)\cos(\gamma)+c^3\cos(\alpha)\cos(\beta)=abc\left(1-2\cos(\alpha)\cos(\beta)\cos(\gamma)\right).\]

Proof:

\begin{align*} &{}\hspace{-10mm}a^3\cos(\beta)\cos(\gamma)+b^3\cos(\alpha)\cos(\gamma)+c^3\cos^2(\alpha)\cos(\beta)\\ &=d^3\sin^3(\alpha)\cos(\beta)\cos(\gamma)+d^3\sin^3(\beta)\cos(\alpha)\cos(\gamma)+d^3\sin^3(\gamma)\cos(\alpha)\cos(\beta)\\ &=d^3\sin^3(\alpha)\cos(\beta)\cos(\gamma)+d^3\sin(\beta)\left(1-\cos^2(\beta)\right)\cos(\alpha)\cos(\gamma) +d^3\sin(\gamma)\left(1-\cos^2(\gamma)\right)\cos(\alpha)\cos(\beta)\\ &=d^3\sin^3(\alpha)\cos(\beta)\cos(\gamma)+\cos(\alpha)\left(\sin(\beta)\cos(\gamma)+\sin(\gamma)\cos(\beta)\right) -\frac{1}{2}\cos(\alpha)\cos(\beta)\cos(\gamma)\left(\sin(2\beta)+\sin(2\gamma)\right)\\ &=d^3\sin^3(\alpha)\cos(\beta)\cos(\gamma)+\cos(\alpha)\sin(\beta+\gamma)-\cos(\alpha)\cos(\beta)\cos(\gamma)\sin(\beta+\gamma)\cos(\beta-\gamma)\\ &=d^3\sin(\alpha)\left(1-\cos^2(\alpha)\right)\cos(\beta)\cos(\gamma)+\cos(\alpha)\sin(\alpha)-\cos(\alpha)\cos(\beta)\cos(\gamma)\sin(\alpha)\cos(\beta-\gamma)\\ &=d^3\sin(\alpha)\left(\left(1-\cos^2(\alpha)\right)\cos(\beta)\cos(\gamma)+\cos(\alpha)-\cos(\alpha)\cos(\beta)\cos(\gamma)\cos(\beta-\gamma)\right)\\ &=d^3\sin(\alpha)\left(\cos(\beta)\cos(\gamma)+\cos(\alpha)-\cos(\alpha)\cos(\beta)\cos(\gamma)\left(\cos(\alpha)+\cos(\beta-\gamma)\right)\right)\\ &=d^3\sin(\alpha)\left(\cos(\beta)\cos(\gamma)-\cos(\beta+\gamma)+\cos(\alpha)\cos(\beta)\cos(\gamma)\left(\cos(\beta+\gamma)-\cos(\beta-\gamma)\right)\right)\\ &=d^3\sin(\alpha)\left(\sin(\beta)\sin(\gamma)-\cos(\alpha)\cos(\beta)\cos(\gamma)\cdot2\sin(\beta)\sin(\gamma)\right)\\ &=d^3\sin(\alpha)\sin(\beta)\sin(\gamma)\left(1-2\cos(\alpha)\cos(\beta)\cos(\gamma)\right)\\ &=abc\left(1-2\cos(\alpha)\cos(\beta)\cos(\gamma)\right). \end{align*}

10)

\[\tan(\alpha)+\tan(\beta)+\tan(\gamma)=\tan(\alpha)\tan(\beta)\tan(\gamma).\]

Proof:

\[\tan(\gamma)=\tan(\pi-\alpha-\beta)=-\tan(\alpha+\beta)=-\frac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)}.\]

Hence:

\begin{align*} \tan(\alpha)+\tan(\beta)+\tan(\gamma)&=\tan(\alpha)+\tan(\beta)-\frac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)}\\ &=\left(\tan(\alpha)+\tan(\beta)\right)\left(1-\frac{1}{1-\tan(\alpha)\tan(\beta)}\right)\\ &=\left(\tan(\alpha)+\tan(\beta)\right)\frac{1-\tan(\alpha)\tan(\beta)-1}{1-\tan(\alpha)\tan(\beta)}\\ &=\left(\tan(\alpha)+\tan(\beta)\right)\left(\frac{-\tan(\alpha)\tan(\beta)}{1-\tan(\alpha)\tan(\beta)}\right)\\ &=\tan(\alpha)\tan(\beta)\left(-\frac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)}\right)\\ &=\tan(\alpha)\tan(\beta)\tan(\gamma). \end{align*}

---

Finally, we have Heron's formula: let \(s=\frac{1}{2}(a+b+c)\) be the semiperimeter of the triangle, then the area of the triangle equals \(\sqrt{s(s-a)(s-b)(s-c)}\).

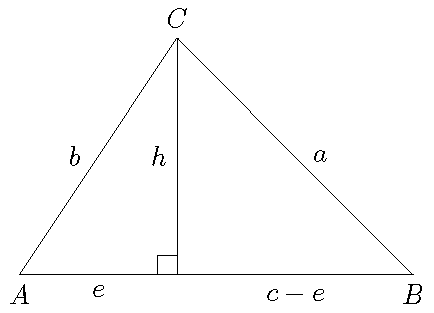
Proof:

Using the Pythagorean theorem, we have: \(h^2=b^2-e^2\) and \(h^2=a^2-(c-e)^2\). This implies that \(b^2-e^2=a^2-(c-e)^2\) or equivalently \(b^2=a^2-c^2+2ce\). Hence, we have: \(e=\displaystyle\frac{b^2+c^2-a^2}{2c}\).

Then we have:

\begin{align*} h^2&=b^2-e^2=b^2-\frac{(b^2+c^2-a^2)^2}{4c^2}=\frac{4b^2c^2-(b^2+c^2-a^2)^2}{4c^2}\\ &=\frac{(2bc+b^2+c^2-a^2)(2bc-b^2-c^2+a^2)}{4c^2}=\frac{\left((b+c)^2-a^2\right)\left(a^2-(b-c)^2\right)}{4c^2}\\ &=\frac{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}{4c^2}. \end{align*}

Now the area of the triangle equals \(\frac{1}{2}ch\) which reads

\[\frac{c}{2}\sqrt{\frac{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}{4c^2}}=\frac{1}{4}\sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}.\]

Let \(s=\displaystyle\frac{a+b+c}{2}\), then: \(s-a=\displaystyle\frac{b+c-a}{2}\), \(s-b=\displaystyle\frac{a+c-b}{2}\) and \(s-c=\displaystyle\frac{a+b-c}{2}\). Now we conclude that the area of the triangle equals

\[\sqrt{\frac{a+b+c}{2}\cdot\frac{b+c-a}{2}\cdot\frac{a+b-c}{2}\cdot\frac{a+c-b}{2}}=\sqrt{s(s-a)(s-b)(s-c)}.\]

---

Last modified on August 23, 2025