Calculus – Trigonometry – Remarkable identities

Taking \(x+y=\alpha\) and \(x-y=\beta\) in

\[\sin(x+y)+\sin(x-y)=2\sin(x)\cos(y)\quad\text{and}\quad\cos(x+y)+\cos(x-y)=2\cos(x)\cos(y)\]

we obtain \(x=(\alpha+\beta)/2\) and \(y=(\alpha-\beta)/2\) and therefore

\[\sin(\alpha)+\sin(\beta)=2\sin\left(\frac{\alpha+\beta}{2}\right)\cos\left(\frac{\alpha-\beta}{2}\right)\quad\text{and}\quad \cos(\alpha)+\cos(\beta)=2\cos\left(\frac{\alpha+\beta}{2}\right)\cos\left(\frac{\alpha-\beta}{2}\right),\]

which implies that

\[\frac{\sin(\alpha)+\sin(\beta)}{\cos(\alpha)+\cos(\beta)}=\tan\left(\frac{\alpha+\beta}{2}\right),\quad\alpha+\beta\ne\pi\;\text{(mod \(2\pi\))}.\]

In the picture below we have \(\alpha=\frac{1}{7}\pi\). In each of the three equilateral triangles we use a rectangular triangle being half of it to find that \(\cos(\frac{1}{7}\pi)=\frac{x+y}{2x}\), \(\cos(\frac{2}{7}\pi)=\frac{x}{2y}\) and \(\cos(\frac{3}{7}\pi)=\frac{y}{2(x+y)}\).

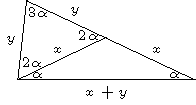
Hence we have:

\[\cos(\tfrac{1}{7}\pi)\cos(\tfrac{2}{7}\pi)\cos(\tfrac{3}{7}\pi)=\frac{x+y}{2x}\cdot\frac{x}{2y}\cdot\frac{y}{2(x+y)}=\frac{1}{8}.\]

Using the double angle formula \(\sin(2x)=2\sin(x)\cos(x)\) twice and \(2\sin(x)\cos(y)=\sin(x+y)+\sin(x-y)\) we also have:

\[\cos(\alpha)\cos(2\alpha)\cos(3\alpha)=\frac{\sin(2\alpha)\cos(2\alpha)\cos(3\alpha)}{2\sin(\alpha)}=\frac{\sin(4\alpha)\cos(3\alpha)}{4\sin(\alpha)} =\frac{\sin(7\alpha)+\sin(\alpha)}{8\sin(\alpha)}=\frac{1}{8},\]

since \(\sin(7\alpha)=\sin(\pi)=0\). It is clear that this result can be generalized to

\[\cos(\tfrac{k}{7}\pi)\cos(\tfrac{2k}{7}\pi)\cos(\tfrac{3k}{7}\pi)=\frac{1}{8},\quad k\in\{\pm1,\pm2,\pm3,\ldots,\pm6\}.\]

Similarly we have:

\[\cos(p)\cos(2p)\cos(4p)\cos(q)=\frac{\sin(8p)\cos(q)}{8\sin(p)}=\frac{\sin(8p+q)+\sin(8p-q)}{16\sin(p)}.\]

Now we have: \(8p+q=k\pi\) and \(8p-q=p\) if \(p=\frac{k}{15}\pi\) and \(q=\frac{7k}{15}\pi\). This implies that

\[\cos(\tfrac{k}{15}\pi)\cos(\tfrac{2k}{15}\pi)\cos(\tfrac{4k}{15})\cos(\tfrac{7k}{15}\pi)=\frac{1}{16}, \quad k\in\{\pm1,\pm2,\pm3,\ldots,\pm14\}.\]

Proceeding in the same way we have:

\[\cos(p)\cos(2p)\cos(4p)\cos(8p)\cos(q)=\frac{\sin(16p)\cos(q)}{16\sin(p)}=\frac{\sin(16p+q)+\sin(16p-q)}{32\sin(p)}.\]

Now we have: \(16p+q=k\pi\) and \(16p-q=p\) if \(p=\frac{k}{31}\pi\) and \(q=\frac{15k}{31}\pi\). This implies that

\[\cos(\tfrac{k}{31}\pi)\cos(\tfrac{2k}{31}\pi)\cos(\tfrac{4k}{31})\cos(\tfrac{8k}{31}\pi)\cos(\tfrac{15k}{31}\pi)=\frac{1}{32}, \quad k\in\{\pm1,\pm2,\pm3,\ldots,\pm30\}.\]

This can be generalized to:

\[\prod_{i=0}^{n-2}\cos\left(\frac{2^i}{2^n-1}k\pi\right)\cdot\cos\left(\frac{2^{n-1}-1}{2^n-1}k\pi\right)=\frac{1}{2^n}, \quad k\in\{\pm1,\pm2,\pm3,\ldots,\pm(2^n-2)\},\quad n=2,3,4,\ldots,\]

where the case \(n=2\) reduces to \(\cos(\frac{k}{3}\pi)\cos(\frac{k}{3}\pi)=\frac{1}{4}\) for \(k=1\) or \(k=2\).

Using the double angle formula \(\sin(2x)=2\sin(x)\cos(x)\) and \(2\sin(x)\cos(y)=\sin(x+y)+\sin(x-y)\) we also have:

\begin{align*} \cos(\alpha)-\cos(2\alpha)+\cos(3\alpha) &=\frac{2\sin(\alpha)\cos(\alpha)-2\sin(\alpha)\cos(2\alpha)+2\sin(\alpha)\cos(3\alpha)}{2\sin(\alpha)}\\ &=\frac{\sin(2\alpha)-\sin(3\alpha)+\sin(\alpha)+\sin(4\alpha)-\sin(2\alpha)}{2\sin(\alpha)}=\frac{\sin(\alpha)+\sin(4\alpha)-\sin(3\alpha)}{2\sin(\alpha)}=\frac{1}{2}, \end{align*}

since \(\sin(4\alpha)=\sin(3\alpha)\) if \(\alpha=\frac{1}{7}\pi\). Since \(\cos(2\alpha)=-\cos(5\alpha)\), this can also be written as

\[\cos(\alpha)+\cos(3\alpha)+\cos(5\alpha)=\frac{1}{2}.\]

A direct proof is similar:

\begin{align*} \cos(\alpha)+\cos(3\alpha)+\cos(5\alpha) &=\frac{2\sin(\alpha)\cos(\alpha)+2\sin(\alpha)\cos(3\alpha)+2\sin(\alpha)\cos(5\alpha)}{2\sin(\alpha)}\\ &=\frac{\sin(2\alpha)+\sin(4\alpha)-\sin(2\alpha)+\sin(6\alpha)-\sin(4\alpha)}{2\sin(\alpha)} =\frac{\sin(6\alpha)}{2\sin(\alpha)}=\frac{1}{2}, \end{align*}

since \(\sin(6\alpha)=\sin(\alpha)\) if \(\alpha=\frac{1}{7}\pi\). This can be generalized to

\[\sum_{k=1}^n\cos\left(\frac{2k-1}{2n+1}\pi\right)=\frac{1}{2},\quad n=1,2,3,\ldots.\]

For \(n=1\) this reads \(\cos(\frac{1}{3}\pi)=\frac{1}{2}\). In order to prove the formula we set \(\alpha=\frac{1}{2n+1}\pi\) to find:

\begin{align*} \sum_{k=1}^n\cos\left(\frac{2k-1}{2n+1}\pi\right)&=\sum_{k=1}^n\cos\left((2k-1)\alpha\right)=\cos(\alpha)+\cos(3\alpha)+\cos(5\alpha)+\cdots+\cos((2n-1)\alpha)\\ &=\frac{2\sin(\alpha)\cos(\alpha)+2\sin(\alpha)\cos(3\alpha)+2\sin(\alpha)\cos(5\alpha)+\cdots+2\sin(\alpha)\cos((2n-1)\alpha)}{2\sin(\alpha)}\\ &=\frac{\sin(2\alpha)+\sin(4\alpha)-\sin(2\alpha)+\sin(6\alpha)-\sin(4\alpha)+\cdots+\sin(2n\alpha)-\sin((2n-2)\alpha)}{2\sin(\alpha)} =\frac{\sin(2n\alpha)}{2\sin(\alpha)}=\frac{1}{2}, \end{align*}

since \(\sin(2n\alpha)=\sin(\alpha)\) if \(\alpha=\frac{1}{2n+1}\pi\). For \(n=2\) we have: \(\cos(\frac{1}{5}\pi)+\cos(\frac{3}{5}\pi)=\frac{1}{2}\). Earlier we have found that \(\cos(\frac{1}{5}\pi)=\frac{1}{4}(1+\sqrt{5})\) and \(\cos(\frac{3}{5}\pi)=\frac{1}{4}(1-\sqrt{5})\), which also implies that \(\cos(\frac{1}{5}\pi)+\cos(\frac{3}{5}\pi)=\frac{1}{2}\).

---

Last modified on October 12, 2022