Calculus – Trigonometry – Identities

The Pythagorean theorem implies that \(\sin^2(\theta)+\cos^2(\theta)=1\) and therefore

\(1+\tan^2(\theta)=\dfrac{1}{\cos^2(\theta)}\) and \(1+\dfrac{1}{\tan^2(\theta)}=\dfrac{1}{\sin^2(\theta)}\).

The sine and cosine are \(2\pi\)-periodic and the tangent is \(\pi\)-periodic:

\(\sin(\theta+2\pi)=\sin(\theta)\), \(\cos(\theta+2\pi)=\cos(\theta)\) and \(\tan(\theta+\pi)=\tan(\theta)\).

The sine and tangent are odd functions and the cosine is an even function, which means that

\(\sin(-\theta)=-\sin(\theta)\), \(\cos(-\theta)=\cos(\theta)\) and \(\tan(-\theta)=-\tan(\theta)\).

Further we have \(\sin(\theta+\frac{1}{2}\pi)=\cos(\theta)\) and \(\cos(\theta+\frac{1}{2}\pi)=-\sin(\theta)\) and the symmetry relations

\(\sin(\pi-\theta)=\sin(\theta)\), \(\cos(\pi-\theta)=-\cos(\theta)\) and \(\tan(\pi-\theta)=-\tan(\theta)\).

Double angle formulas

\(\sin(2x)=2\sin(x)\cos(x),\quad\cos(2x)=\cos^2(x)-\sin^2(x)=1-2\sin^2(x)=2\cos^2(x)-1\).

\(2\sin^2(x)=1-\cos(2x),\quad2\cos^2(x)=1+\cos(2x)\).

Summation formulas

\(\sin(x+y)=\sin(x)\cos(y)+\cos(x)\sin(y),\quad\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)\).

\(\sin(x-y)=\sin(x)\cos(y)-\cos(x)\sin(y),\quad\cos(x-y)=\cos(x)\cos(y)+\sin(x)\sin(y)\).

\(\tan(x+y)=\dfrac{\tan(x)+\tan(y)}{1-\tan(x)\tan(y)},\quad\tan(x-y)=\dfrac{\tan(x)-\tan(y)}{1+\tan(x)\tan(y)}\).

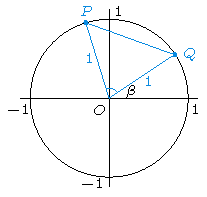
In order to prove these formulas, we consider the picture above with blue angle \(\alpha-\beta\). Hence, we have: \(P=(\cos(\alpha),\sin(\alpha))\) and \(Q=(\cos(\beta),\sin(\beta))\). The distance between \(P\) and \(Q\) can be computed using the law of cosines:

\[(PQ)^2=(OP)^2+(OQ)^2-2(OP)(OQ)\cos(\alpha-\beta)=2-2\cos(\alpha-\beta).\]

On the other hand, this distance can be computed as

\begin{align*} (PQ)^2&=(\cos(\beta)-\cos(\alpha))^2+(\sin(\beta)-\sin(\alpha))^2\\ &=\cos^2(\beta)-2\cos(\alpha)\cos(\beta)+\cos^2(\alpha)+\sin^2(\beta)-2\sin(\alpha)\sin(\beta)+\sin^2(\alpha)\\ &=2-2\left(\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)\right). \end{align*}

This implies that \(\cos(\alpha-\beta)=\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)\).

Replacing \(\beta\) with \(-\beta\) we obtain that \(\cos(\alpha+\beta)=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)\).

Using \(\sin(\beta+\frac{1}{2}\pi)=\cos(\beta)\) and \(\cos(\beta+\frac{1}{2}\pi)=-\sin(\beta)\) we obtain

\begin{align*} \sin(\alpha+\beta)&=-\cos(\alpha+\beta+\tfrac{1}{2}\pi)=\sin(\alpha)\sin(\beta+\tfrac{1}{2}\pi)-\cos(\alpha)\cos(\beta+\tfrac{1}{2}\pi)\\ &=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta). \end{align*}

Replacing \(\beta\) with \(-\beta\) we obtain that \(\sin(\alpha-\beta)=\sin(\alpha)\cos(\beta)-\cos(\alpha)\sin(\beta)\).

Now the summation formulas for the tangent follow from these summation formulas for the sine and the cosine:

\begin{align*} \tan(x+y)&=\frac{\sin(x+y)}{\cos(x+y)}=\frac{\sin(x)\cos(y)+\cos(x)\sin(y)}{\cos(x)\cos(y)-\sin(x)\sin(y)}\\ &=\frac{\frac{\sin(x)\cos(y)}{\cos(x)\cos(y)}+\frac{\cos(x)\sin(y)}{\cos(x)\cos(y)}}{\frac{\cos(x)\cos(y)}{\cos(x)\cos(y)}-\frac{\sin(x)\sin(y)}{\cos(x)\cos(y)}} =\frac{\frac{\sin(x)}{\cos(x)}+\frac{\sin(y)}{\cos(y)}}{1-\frac{\sin(x)}{\cos(x)}\frac{\sin(y)}{\cos(y)}}=\frac{\tan(x)+\tan(y)}{1-\tan(x)\tan(y)}. \end{align*}

Finally, replacing \(y\) with \(-y\) we obtain: \(\tan(x-y)=\dfrac{\tan(x)-\tan(y)}{1+\tan(x)\tan(y)}\).

The double angle formulas are special cases of these summation formulas.

Combinations lead to \(2\sin(x)\cos(y)=\sin(x+y)+\sin(x-y)\),

\[2\cos(x)\cos(y)=\cos(x+y)+\cos(x-y)\quad\text{and}\quad2\sin(x)\sin(y)=\cos(x-y)-\cos(x+y)\]

Further we have

\[2\sin(x+y)\cos(x-y)=\sin(2x)+\sin(2y)\quad\text{and}\quad2\cos(x+y)\sin(x-y)=\sin(2x)-\sin(2y).\]

Finally, we deduce that

\begin{align*} \cos(x+y)\cos(x-y)&=\left(\cos(x)\cos(y)-\sin(x)\sin(y)\right)\left(\cos(x)\cos(y)+\sin(x)\sin(y)\right)\\ &=\cos^2(x)\cos^2(y)-\sin^2(x)\sin^2(y)=\cos^2(x)\left(1-\sin^2(y)\right)-\left(1-\cos^2(x)\right)\sin^2(y)\\ &=\cos^2(x)-\sin^2(y). \end{align*} \begin{align*} \cos(x+y)\cos(x-y)&=\left(\cos(x)\cos(y)-\sin(x)\sin(y)\right)\left(\cos(x)\cos(y)+\sin(x)\sin(y)\right)\\ &=\cos^2(x)\cos^2(y)-\sin^2(x)\sin^2(y)=\left(1-\sin^2(x)\right)\cos^2(y)-\sin^2(x)\left(1-\cos^2(y)\right)\\ &=\cos^2(y)-\sin^2(x). \end{align*} \begin{align*} \sin(x+y)\sin(x-y)&=\left(\sin(x)\cos(y)+\cos(x)\sin(y)\right)\left(\sin(x)\cos(y)-\cos(x)\sin(y)\right)\\ &=\sin^2(x)\cos^2(y)-\cos^2(x)\sin^2(y)=\sin^2(x)\left(1-\sin^2(y)\right)-\left(1-\sin^2(x)\right)\sin^2(y)\\ &=\sin^2(x)-\sin^2(y). \end{align*} \begin{align*} \sin(x+y)\sin(x-y)&=\left(\sin(x)\cos(y)+\cos(x)\sin(y)\right)\left(\sin(x)\cos(y)-\cos(x)\sin(y)\right)\\ &=\sin^2(x)\cos^2(y)-\cos^2(x)\sin^2(y)=\left(1-\cos^2(x)\right)\cos^2(y)-\cos^2(x)\left(1-\cos^2(y)\right)\\ &=\cos^2(y)-\cos^2(x). \end{align*}

---

Last modified on October 4, 2025