Analyse – Goniometrie – Gelijkheden

Uit de stelling van Pythagoras volgt dat \(\sin^2(\theta)+\cos^2(\theta)=1\) en dus

\(1+\tan^2(\theta)=\dfrac{1}{\cos^2(\theta)}\) en \(1+\dfrac{1}{\tan^2(\theta)}=\dfrac{1}{\sin^2(\theta)}\).

De sinus en de cosinus zijn \(2\pi\)-periodiek en de tangens is \(\pi\)-periodiek:

\(\sin(\theta+2\pi)=\sin(\theta)\), \(\cos(\theta+2\pi)=\cos(\theta)\) en \(\tan(\theta+\pi)=\tan(\theta)\).

De sinus en de tangens zijn oneven functies en de cosinus is een even functie. Dit betekent dat

\(\sin(-\theta)=-\sin(\theta)\), \(\cos(-\theta)=\cos(\theta)\) en \(\tan(-\theta)=-\tan(\theta)\).

Verder geldt \(\sin(\theta+\frac{1}{2}\pi)=\cos(\theta)\) en \(\cos(\theta+\frac{1}{2}\pi)=-\sin(\theta)\) en de symmetrie relaties

\(\sin(\pi-\theta)=\sin(\theta)\), \(\cos(\pi-\theta)=-\cos(\theta)\) en \(\tan(\pi-\theta)=-\tan(\theta)\).

Dubbele-hoekformules

\(\sin(2x)=2\sin(x)\cos(x),\quad\cos(2x)=\cos^2(x)-\sin^2(x)=1-2\sin^2(x)=2\cos^2(x)-1\).

\(2\sin^2(x)=1-\cos(2x),\quad2\cos^2(x)=1+\cos(2x)\).

Sommatieformules

\(\sin(x+y)=\sin(x)\cos(y)+\cos(x)\sin(y),\quad\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)\).

\(\sin(x-y)=\sin(x)\cos(y)-\cos(x)\sin(y),\quad\cos(x-y)=\cos(x)\cos(y)+\sin(x)\sin(y)\).

\(\tan(x+y)=\dfrac{\tan(x)+\tan(y)}{1-\tan(x)\tan(y)},\quad\tan(x-y)=\dfrac{\tan(x)-\tan(y)}{1+\tan(x)\tan(y)}\).

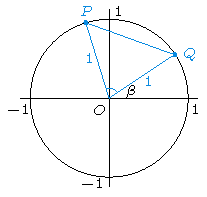
Om deze formules te bewijzen, beschouwen we het plaatje hierboven met blauwe hoek \(\alpha-\beta\). Dus geldt: \(P=(\cos(\alpha),\sin(\alpha))\) en \(Q=(\cos(\beta),\sin(\beta))\). De afstand tussen \(P\) en \(Q\) kan worden berekend met behulp van de cosinusregel:

\[(PQ)^2=(OP)^2+(OQ)^2-2(OP)(OQ)\cos(\alpha-\beta)=2-2\cos(\alpha-\beta).\]

Echter, deze afstand kan ook worden berekend als

\begin{align*} (PQ)^2&=(\cos(\beta)-\cos(\alpha))^2+(\sin(\beta)-\sin(\alpha))^2\\ &=\cos^2(\beta)-2\cos(\alpha)\cos(\beta)+\cos^2(\alpha)+\sin^2(\beta)-2\sin(\alpha)\sin(\beta)+\sin^2(\alpha)\\ &=2-2\left(\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)\right). \end{align*}

Hieruit volgt dat \(\cos(\alpha-\beta)=\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)\).

Vervangen we \(\beta\) door \(-\beta\) dan volgt dat \(\cos(\alpha+\beta)=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)\).

Met behulp van \(\sin(\beta+\frac{1}{2}\pi)=\cos(\beta)\) en \(\cos(\beta+\frac{1}{2}\pi)=-\sin(\beta)\) vinden we

\begin{align*} \sin(\alpha+\beta)&=-\cos(\alpha+\beta+\tfrac{1}{2}\pi)=\sin(\alpha)\sin(\beta+\tfrac{1}{2}\pi)-\cos(\alpha)\cos(\beta+\tfrac{1}{2}\pi)\\ &=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta). \end{align*}

Vervangen we \(\beta\) door \(-\beta\) dan volgt dat \(\sin(\alpha-\beta)=\sin(\alpha)\cos(\beta)-\cos(\alpha)\sin(\beta)\).

Nu volgen de sommatieformules voor de tangens uit deze sommatieformules voor de sinus en de cosinus:

\begin{align*} \tan(x+y)&=\frac{\sin(x+y)}{\cos(x+y)}=\frac{\sin(x)\cos(y)+\cos(x)\sin(y)}{\cos(x)\cos(y)-\sin(x)\sin(y)}\\ &=\frac{\frac{\sin(x)\cos(y)}{\cos(x)\cos(y)}+\frac{\cos(x)\sin(y)}{\cos(x)\cos(y)}}{\frac{\cos(x)\cos(y)}{\cos(x)\cos(y)}-\frac{\sin(x)\sin(y)}{\cos(x)\cos(y)}} =\frac{\frac{\sin(x)}{\cos(x)}+\frac{\sin(y)}{\cos(y)}}{1-\frac{\sin(x)}{\cos(x)}\frac{\sin(y)}{\cos(y)}}=\frac{\tan(x)+\tan(y)}{1-\tan(x)\tan(y)}. \end{align*}

Ten slotte, vervangen we \(y\) door \(-y\) dan volgt: \(\tan(x-y)=\dfrac{\tan(x)-\tan(y)}{1+\tan(x)\tan(y)}\).

De dubbele-hoekformules zijn speciale gevallen van deze sommatieformules.

Combinaties leiden tot \(2\sin(x)\cos(y)=\sin(x+y)+\sin(x-y)\),

\[2\cos(x)\cos(y)=\cos(x+y)+\cos(x-y)\quad\text{en}\quad2\sin(x)\sin(y)=\cos(x-y)-\cos(x+y)\]

Verder geldt

\[2\sin(x+y)\cos(x-y)=\sin(2x)+\sin(2y)\quad\text{en}\quad2\cos(x+y)\sin(x-y)=\sin(2x)-\sin(2y).\]

Ten slotte leiden we af dat

\begin{align*} \cos(x+y)\cos(x-y)&=\left(\cos(x)\cos(y)-\sin(x)\sin(y)\right)\left(\cos(x)\cos(y)+\sin(x)\sin(y)\right)\\ &=\cos^2(x)\cos^2(y)-\sin^2(x)\sin^2(y)=\cos^2(x)\left(1-\sin^2(y)\right)-\left(1-\cos^2(x)\right)\sin^2(y)\\ &=\cos^2(x)-\sin^2(y). \end{align*} \begin{align*} \cos(x+y)\cos(x-y)&=\left(\cos(x)\cos(y)-\sin(x)\sin(y)\right)\left(\cos(x)\cos(y)+\sin(x)\sin(y)\right)\\ &=\cos^2(x)\cos^2(y)-\sin^2(x)\sin^2(y)=\left(1-\sin^2(x)\right)\cos^2(y)-\sin^2(x)\left(1-\cos^2(y)\right)\\ &=\cos^2(y)-\sin^2(x). \end{align*} \begin{align*} \sin(x+y)\sin(x-y)&=\left(\sin(x)\cos(y)+\cos(x)\sin(y)\right)\left(\sin(x)\cos(y)-\cos(x)\sin(y)\right)\\ &=\sin^2(x)\cos^2(y)-\cos^2(x)\sin^2(y)=\sin^2(x)\left(1-\sin^2(y)\right)-\left(1-\sin^2(x)\right)\sin^2(y)\\ &=\sin^2(x)-\sin^2(y). \end{align*} \begin{align*} \sin(x+y)\sin(x-y)&=\left(\sin(x)\cos(y)+\cos(x)\sin(y)\right)\left(\sin(x)\cos(y)-\cos(x)\sin(y)\right)\\ &=\sin^2(x)\cos^2(y)-\cos^2(x)\sin^2(y)=\left(1-\cos^2(x)\right)\cos^2(y)-\cos^2(x)\left(1-\cos^2(y)\right)\\ &=\cos^2(y)-\cos^2(x). \end{align*}

---

Laatst gewijzigd op 4 oktober 2025