Analyse – Goniometrie

De stelling van Thales

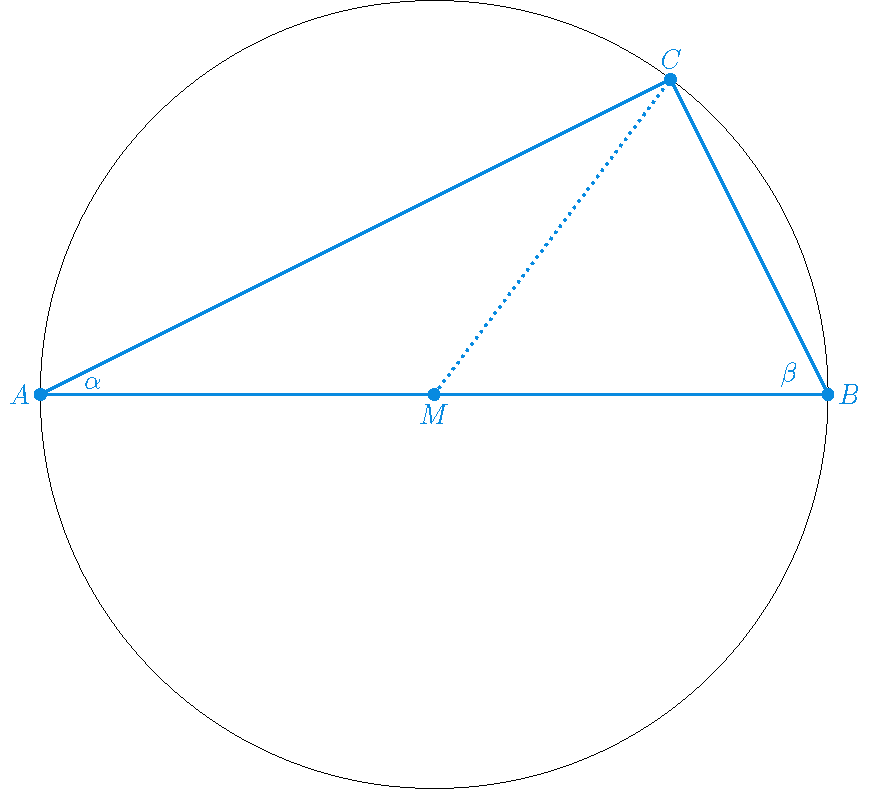
Als \(AB\) een middellijn is van een cirkel en \(C\) is een willekeurig punt op de cirkel, niet gelijk aan \(A\) of \(B\), dan geldt dat de hoek \(ACB\) gelijk is aan \(90^{\circ}\).

Bewijs: Beschouw de hoeken \(\alpha\) en \(\beta\) zoals aangegeven in bovenstaand plaatje. Omdat de driehoek \(AMC\) gelijkbenig is (\(AM\) en \(MC\) zijn beide gelijk aan de straal van de cirkel), geldt: \(\angle ACM=\alpha\). Evenzo is de driehoek \(BMC\) gelijkbenig (\(BM\) en \(MC\) zijn beide gelijk aan de straal van de cirkel) en dus: \(\angle BCM=\beta\). We moeten dus bewijzen dat \(\alpha+\beta\) gelijk is aan \(90^{\circ}\).

Nu geldt: \(\angle AMC=180^{\circ}-2\alpha\) en \(\angle BMC=180^{\circ}-2\beta\). Verder is: \(\angle AMC+\angle BMC=180^{\circ}\). Dus:

\[180^{\circ}-2\alpha+180^{\circ}-2\beta=180^{\circ}\quad\Longleftrightarrow\quad 180^{\circ}-2\alpha-2\beta=0 \quad\Longleftrightarrow\quad\alpha+\beta=90^{\circ.}\]

Hoeken
Hoeken kunnen worden gemeten in graden en in radialen (afgekort als rad). De hoek gegeven door een volledige omwenteling bedraagt \(360^{\circ}\), hetgeen overeenkomt met \(2\pi\) rad. Dus:

\(\pi\;\text{rad}=180^{\circ}\quad\Longrightarrow\quad 1\;\text{rad}=\left(\dfrac{180}{\pi}\right)^{\circ}\quad\text{en}\quad 1^{\circ}=\dfrac{\pi}{180}\;\text{rad}\).

In de analyse gebruiken we radialen om hoeken te meten tenzij anders aangegeven. Tevens laten we dan "rad" achterwege.

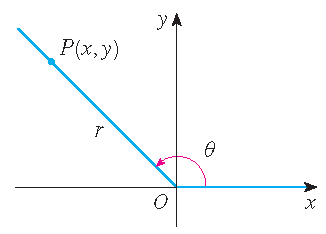The standaardpositie van een hoek ontstaat als we het hoekpunt in de oorsprong van een coördinaatstelsel plaatsen en de beginpositie op de positieve \(x\)-as. Een positieve hoek wordt dan verkregen door de beginpositie tegen de wijzers van de klok in te draaien totdat deze overeenkomt met de eindpositie. Evenzo worden negatieve hoeken verkregen door met de wijzers van de klok mee te draaien.

Voor een willekeurige hoek \(\theta\) in standaardpositie laat \(P(x,y)\) een willekeurig punt op de eindpositie van \(\theta\) en laat \(r\) de afstand tussen \(O\) en \(P\) zijn. Dan definiëren we:

\(\sin(\theta)=\dfrac{y}{r},\quad\cos(\theta)=\dfrac{x}{r}\quad\text{en}\quad\tan(\theta)=\dfrac{\sin(\theta)}{\cos(\theta)}=\dfrac{y}{x}\quad(x\neq0)\).

Standaardwaarden

\(\theta\) (in graden)	\(0^{\circ}\)	\(30^{\circ}\)	\(45^{\circ}\)	\(60^{\circ}\)	\(90^{\circ}\)	\(120^{\circ}\)	\(135^{\circ}\)	\(150^{\circ}\)	\(180^{\circ}\)	\(270^{\circ}\)	\(360^{\circ}\)
\(\theta\) (in radialen)	\(0\)	\(\frac{1}{6}\pi\)	\(\frac{1}{4}\pi\)	\(\frac{1}{3}\pi\)	\(\frac{1}{2}\pi\)	\(\frac{2}{3}\pi\)	\(\frac{3}{4}\pi\)	\(\frac{5}{6}\pi\)	\(\pi\)	\(\frac{3}{2}\pi\)	\(2\pi\)
\(\sin(\theta)\)	\(0\)	\(\frac{1}{2}\)	\(\frac{1}{2}\sqrt{2}\)	\(\frac{1}{2}\sqrt{3}\)	\(1\)	\(\frac{1}{2}\sqrt{3}\)	\(\frac{1}{2}\sqrt{2}\)	\(\frac{1}{2}\)	\(0\)	\(-1\)	\(0\)
\(\cos(\theta)\)	\(1\)	\(\frac{1}{2}\sqrt{3}\)	\(\frac{1}{2}\sqrt{2}\)	\(\frac{1}{2}\)	\(0\)	\(-\frac{1}{2}\)	\(-\frac{1}{2}\sqrt{2}\)	\(-\frac{1}{2}\sqrt{3}\)	\(-1\)	\(0\)	\(1\)
\(\tan(\theta)\)	\(0\)	\(\frac{1}{3}\sqrt{3}\)	\(1\)	\(\sqrt{3}\)	\(-\)	\(-\sqrt{3}\)	\(-1\)	\(-\frac{1}{3}\sqrt{3}\)	\(0\)	\(-\)	\(0\)

Grafieken

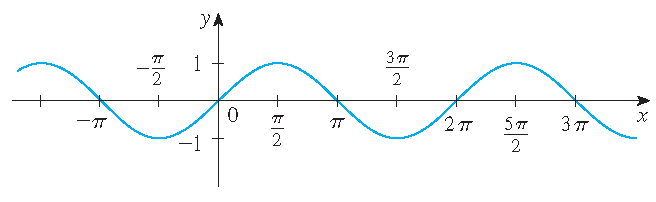
\(y=\sin(x)\)

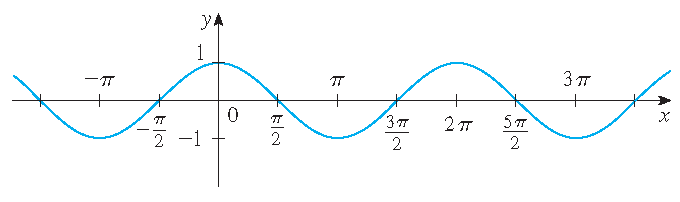
\(y=\cos(x)\)

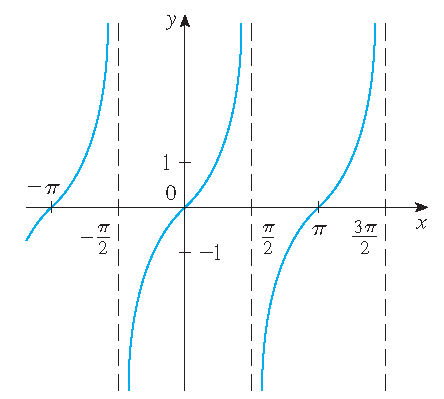
\(y=\tan(x)\)

---

Laatst gewijzigd op 12 oktober 2025