Calculus – Trigonometry

Thales's theorem

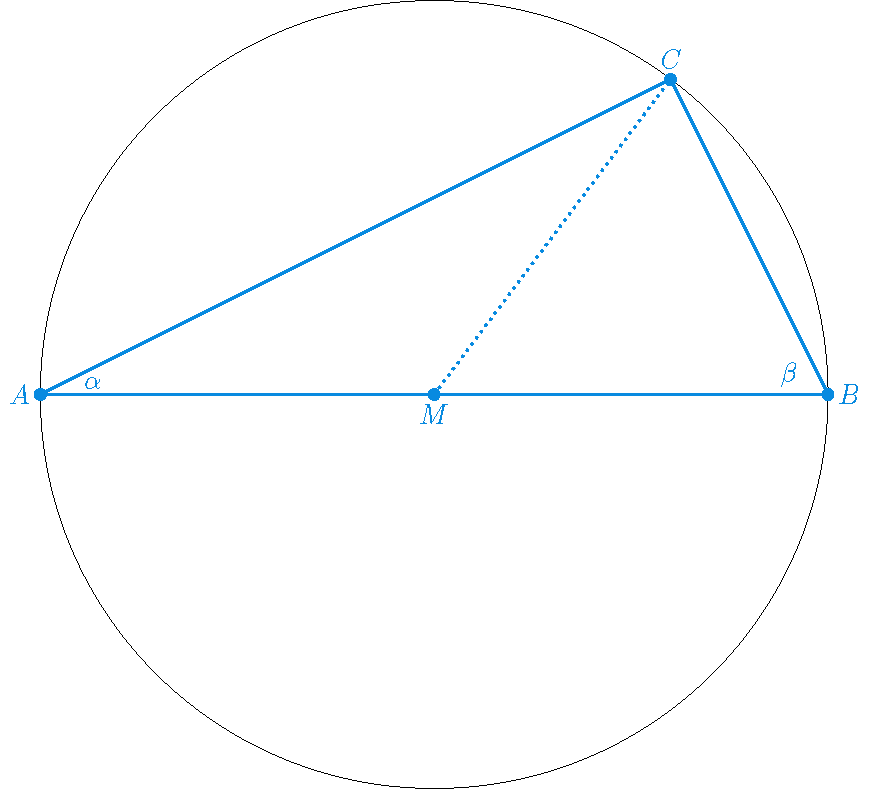
If \(AB\) is a diameter of a circle and \(C\) is an arbitrary point on the circle, not equal to \(A\) or \(B\), then the angle \(ACB\) equals \(90^{\circ}\).

Proof: Consider the angles \(\alpha\) and \(\beta\) as indicated in the picture above. Since the triangle \(AMC\) is isosceles (\(AM\) and \(MC\) are both equal to the radius of the circle), we have: \(\angle ACM=\alpha\). Likewise, the triangle \(BMC\) is isosceles (\(BM\) and \(MC\) are both equal to the radius of the circle) and therefore: \(\angle BCM=\beta\). So, we have to prove that \(\alpha+\beta\) equals \(90^{\circ}\).

Now we have: \(\angle AMC=180^{\circ}-2\alpha\) and \(\angle BMC=180^{\circ}-2\beta\). Further we have: \(\angle AMC+\angle BMC=180^{\circ}\). Hence:

\[180^{\circ}-2\alpha+180^{\circ}-2\beta=180^{\circ}\quad\Longleftrightarrow\quad 180^{\circ}-2\alpha-2\beta=0 \quad\Longleftrightarrow\quad\alpha+\beta=90^{\circ.}\]

Angles
Angles can be measured in degrees or in radians (abbreviated as rad). The angle given by a complete revolution contains \(360^{\circ}\), which is the same as \(2\pi\) rad. Therefore:

\(\pi\;\text{rad}=180^{\circ}\quad\Longrightarrow\quad 1\;\text{rad}=\left(\dfrac{180}{\pi}\right)^{\circ}\quad\text{and}\quad 1^{\circ}=\dfrac{\pi}{180}\;\text{rad}\).

In calculus we use radians to measure angles except when otherwise indicated. Moreover, we then skip "rad".

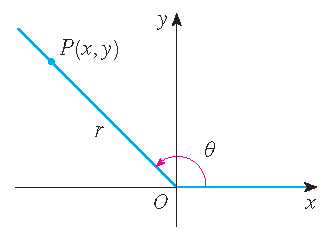The standard position of an angle occurs when we place its vertex at the origin of a coordinate system and its initial side on the positive \(x\)-axis. A positive angle is obtained by rotating the initial side counterclockwise until it coincides with the terminal side. Likewise, negative angles are obtained by clockwise rotation.

For a general angle \(\theta\) in standard position we let \(P(x,y)\) be any point on the terminal side of \(\theta\) and we let \(r\) be the distance between \(O\) and \(P\). Then we define:

\(\sin(\theta)=\dfrac{y}{r},\quad\cos(\theta)=\dfrac{x}{r}\quad\text{and}\quad\tan(\theta)=\dfrac{\sin(\theta)}{\cos(\theta)}=\dfrac{y}{x}\quad(x\neq0)\).

Standard values

\(\theta\) (in degrees)	\(0^{\circ}\)	\(30^{\circ}\)	\(45^{\circ}\)	\(60^{\circ}\)	\(90^{\circ}\)	\(120^{\circ}\)	\(135^{\circ}\)	\(150^{\circ}\)	\(180^{\circ}\)	\(270^{\circ}\)	\(360^{\circ}\)
\(\theta\) (in radians)	\(0\)	\(\frac{1}{6}\pi\)	\(\frac{1}{4}\pi\)	\(\frac{1}{3}\pi\)	\(\frac{1}{2}\pi\)	\(\frac{2}{3}\pi\)	\(\frac{3}{4}\pi\)	\(\frac{5}{6}\pi\)	\(\pi\)	\(\frac{3}{2}\pi\)	\(2\pi\)
\(\sin(\theta)\)	\(0\)	\(\frac{1}{2}\)	\(\frac{1}{2}\sqrt{2}\)	\(\frac{1}{2}\sqrt{3}\)	\(1\)	\(\frac{1}{2}\sqrt{3}\)	\(\frac{1}{2}\sqrt{2}\)	\(\frac{1}{2}\)	\(0\)	\(-1\)	\(0\)
\(\cos(\theta)\)	\(1\)	\(\frac{1}{2}\sqrt{3}\)	\(\frac{1}{2}\sqrt{2}\)	\(\frac{1}{2}\)	\(0\)	\(-\frac{1}{2}\)	\(-\frac{1}{2}\sqrt{2}\)	\(-\frac{1}{2}\sqrt{3}\)	\(-1\)	\(0\)	\(1\)
\(\tan(\theta)\)	\(0\)	\(\frac{1}{3}\sqrt{3}\)	\(1\)	\(\sqrt{3}\)	\(-\)	\(-\sqrt{3}\)	\(-1\)	\(-\frac{1}{3}\sqrt{3}\)	\(0\)	\(-\)	\(0\)

Graphs

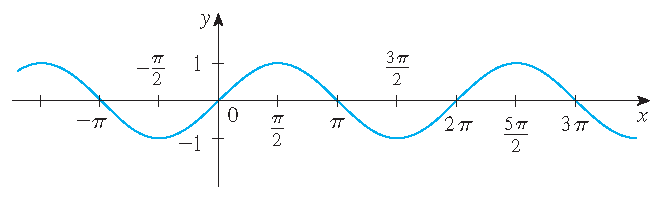
\(y=\sin(x)\)

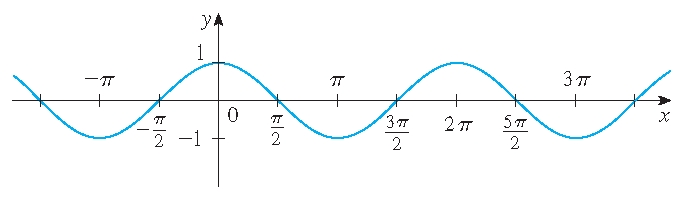
\(y=\cos(x)\)

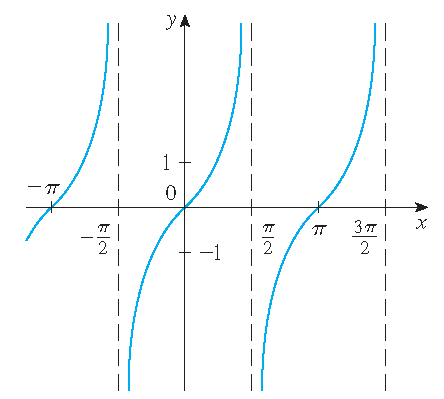
\(y=\tan(x)\)

---

Last modified on October 12, 2025