Analyse – Goniometrie – De stelling van Pythagoras
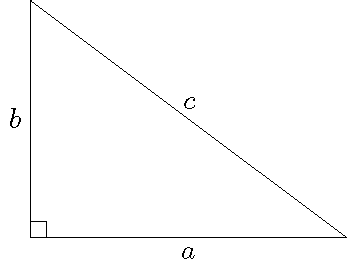
Stelling: In een rechthoekige driehoek met rechthoekszijden \(a\) en \(b\) en schuine zijde \(c\) geldt: \(a^2+b^2=c^2\).
Bewijs: Een elegant bewijs van de stelling van Pythagoras is gebaseerd op het volgende plaatje:
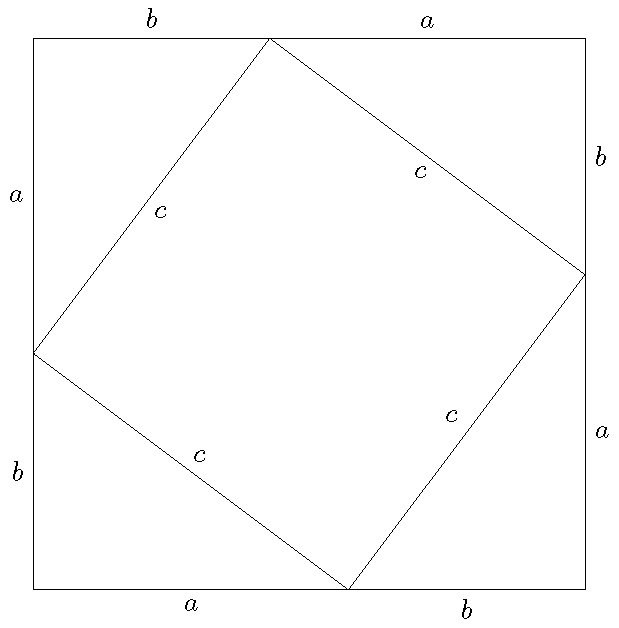
De oppervlakte van het grote vierkant is \((a+b)^2\) en die van het kleine vierkant \(c^2\). De oppervlakte van één van de vier driehoeken is \(\frac{1}{2}ab\). Er geldt dus:
\[(a+b)^2=c^2+4\cdot\tfrac{1}{2}ab\quad\Longleftrightarrow\quad a^2+2ab+b^2=c^2+2ab\quad\Longleftrightarrow\quad a^2+b^2=c^2.\]De cosinusregel is een generalisatie van de stelling van Pythagoras:
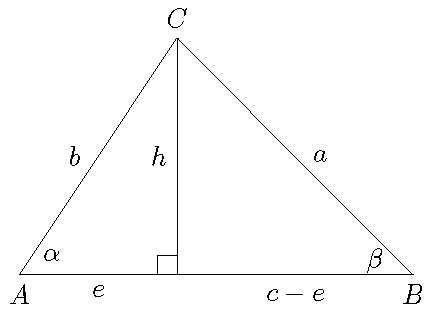
Stelling: In een willekeurige driehoek geldt: \(a^2=b^2+c^2-2bc\cos(\alpha)\).
Bewijs: In bovenstaande figuur geldt volgens de stelling van Pythagoras: \(h^2=b^2-e^2\) en \(h^2=a^2-(c-e)^2\). Dus: \[b^2-e^2=a^2-c^2+2ce-e^2\quad\Longleftrightarrow\quad b^2=a^2-c^2+2ce.\]
Nu geldt: \(\cos(\alpha)=\dfrac{e}{b}\), waaruit volgt dat \(e=b\cos(\alpha)\). Dus:
\[a^2=b^2+c^2-2bc\cos(\alpha).\]Verder geldt de sinusregel:
Stelling: In een willekeurige driehoek geldt: \(\dfrac{a}{\sin(\alpha)}=\dfrac{b}{\sin(\beta)}\).
Bewijs: In bovenstaande figuur geldt: \(\sin(\alpha)=\dfrac{h}{b}\) en \(\sin(\beta)=\dfrac{h}{a}\). Dus: \(b\sin(\alpha)=h=a\sin(\beta)\) oftewel \(\dfrac{a}{\sin(\alpha)}=\dfrac{b}{\sin(\beta)}\).
Het laatste resultaat kan nog worden uitgebreid met:
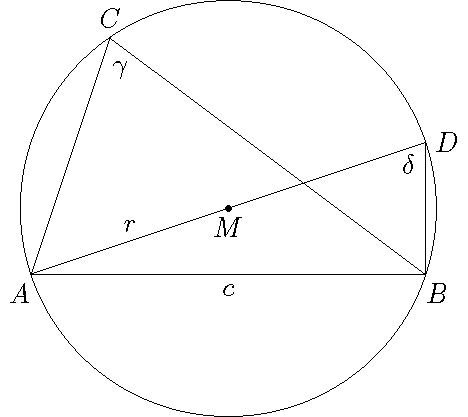
Stelling: \(\dfrac{c}{\sin(\gamma)}=2r\) met \(r\) de straal van de omgeschreven cirkel van de driehoek.
Bewijs: Beschouw het lijnstuk \(AD\) door het middelpunt \(M\) van de omgeschreven cirkel van de driehoek. Volgens de stelling van Thales is de driehoek \(ABD\) dan een rechthoekige driehoek. Omdat \(C\) en \(D\) twee punten zijn op dezelfde cirkel, die verbonden zijn met dezelfde koorde \(AB\) geldt: \(\gamma=\delta\). Dan volgt:
\[\sin(\gamma)=\sin(\delta)=\frac{c}{2r}\quad\Longleftrightarrow\quad\frac{c}{\sin(\gamma)}=2r.\]Laatst gewijzigd op 4 oktober 2025
 Onderwijs
Onderwijs

