Speciale Functies – Orthogonale polynomen – Hermite polynomen
De Hermite polynomen zijn orthogonaal op het interval \((-\infty,\infty)=\mathbb{R}\) met betrekking tot de normale verdeling \(w(x)=e^{-x^2}\). Deze kunnen worden gedefinieerd door hun Rodrigues formule:
\[H_n(x)=\frac{(-1)^n}{w(x)}D^nw(x)=(-1)^ne^{x^2}D^ne^{-x^2},\quad n=0,1,2,\ldots.\tag1\]Omdat \(D^{n+1}=D\,D^n\), geldt
\begin{align*} D^{n+1}w(x)&=D\left[D^nw(x)\right]=(-1)^nD\left[w(x)H_n(x)\right]=(-1)^n\left[w'(x)H_n(x)+w(x)H_n'(x)\right]\\[2.5mm] &=(-1)^{n+1}w(x)\left[2xH_n(x)-H_n'(x)\right],\quad n=0,1,2,\ldots, \end{align*}waaruit volgt dat
\[H_{n+1}(x)=2xH_n(x)-H_n'(x),\quad n=0,1,2,\ldots.\tag2\]Uit de definitie (1) volgt dat \(H_0(x)=1\). Dan volgt uit (2) met inductie dat \(H_n(x)\) een polynoom van graad \(n\) is. Verder geldt dat \(H_{2n}(x)\) even is en dat \(H_{2n+1}(x)\) oneven is en dat de kopcoëfficiënt van het polynoom \(H_n(x)\) gelijk is aan \(k_n=2^n\).
De Hermite polynomen voldoen aan de orthogonaliteitsrelatie
\[\frac{1}{\sqrt{\pi}}\int_{-\infty}^{\infty}e^{-x^2}H_m(x)H_n(x)\,dx=2^n\,n!\,\delta_{mn},\quad m,n\in\{0,1,2,\ldots\}.\tag3\]Om dit te bewijzen gebruiken we de definitie (1) en vinden dat
\[\int_{-\infty}^{\infty}e^{-x^2}H_m(x)H_n(x)\,dx=(-1)^n\int_{-\infty}^{\infty}H_m(x)D^ne^{-x^2}\,dx.\]Nu passen we \(n\) keer partiële integratie toe en concluderen dat de integraal nul wordt voor \(m < n\).
Voor \(m=n\) volgt met behulp van partiële integratie
\[\int_{-\infty}^{\infty}e^{-x^2}H_n(x)H_n(x)\,dx=(-1)^n\int_{-\infty}^{\infty}H_n(x)D^ne^{-x^2}\,dx =\int_{-\infty}^{\infty}D^nH_n(x)\cdot e^{-x^2}\,dx=k_n\,n!\,\int_{-\infty}^{\infty}e^{-x^2}\,dx=2^n\,n!\,\sqrt{\pi}.\]Dit bewijst de orthogonaliteitsrelatie (3).
Om de drieterms recurrente betrekking af te leiden, beginnen we met
\[w(x)=e^{-x^2}\quad\Longrightarrow\quad w'(x)=-2xw(x).\]Dan volgt met behulp van de regel van Leibniz dat
\[D^{n+1}w(x)=D^nw'(x)=D^n\left[-2xw(x)\right]=-2xD^nw(x)-2nD^{n-1}w(x),\]waaruit volgt dat
\[H_{n+1}(x)=2xH_n(x)-2nH_{n-1}(x),\quad n=1,2,3,\ldots.\tag4\]Combineren van (2) en (4) levert dat
\[H_n'(x)=2nH_{n-1}(x),\quad n=1,2,3,\ldots.\tag5\]Differentiëren van (2) geeft
\[H_{n+1}'(x)=2xH_n'(x)+2H_n(x)-H_n''(x),\quad n=0,1,2,\ldots.\]Met behulp van (5) concluderen we dat
\[2(n+1)H_n(x)=2xH_n'(x)+2H_n(x)-H_n''(x),\quad n=0,1,2,\ldots,\]waaruit volgt dat \(H_n(x)\) voldoet aan de tweede orde lineaire differentiaalvergelijking
\[y''(x)-2xy'(x)+2ny(x)=0,\quad n\in\{0,1,2,\ldots\}.\]Ten slotte bewijzen we nog de genererende functie
\[e^{2xt-t^2}=\sum_{n=0}^{\infty}\frac{H_n(x)}{n!}\,t^n.\tag6\]We beginnen met
\[f(t)=e^{-(x-t)^2}=e^{-x^2}\cdot e^{2xt-t^2}.\]De Taylorreeks voor \(f(t)\) is
\[f(t)=\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}\,t^n\]met, met behulp van de substitutie \(x-t=u\),
\[f^{(n)}(0)=\left[\frac{d^n}{dt^n}\,e^{-(x-t)^2}\right]_{t=0} =(-1)^n\left[\frac{d^n}{du^n}\,e^{-u^2}\right]_{u=x}=(-1)^nD^ne^{-x^2}=e^{-x^2}H_n(x),\quad n=0,1,2,\ldots.\]Dus geldt
\[e^{-x^2}\cdot e^{2xt-t^2}=e^{-(x-t)^2}=f(t)=\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}\,t^n =e^{-x^2}\sum_{n=0}^{\infty}\frac{H_n(x)}{n!}\,t^n.\]Dit bewijst de genererende functie (6).
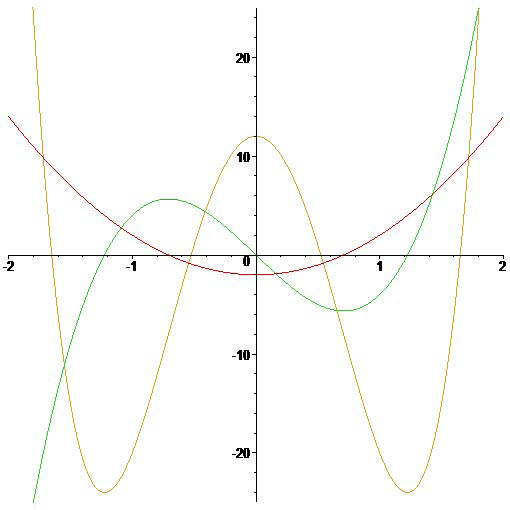
De Hermite polynomen \(H_2(x)\), \(H_3(x)\) en \(H_4(x)\).
Last modified on 22 mei 2021
 Onderwijs
Onderwijs

