Differentiaalvergelijkingen – Stelsels lineaire differentiaalvergelijkingen – Toepassingen

1) Beschouw de gekoppelde vaten getoond in het plaatje:

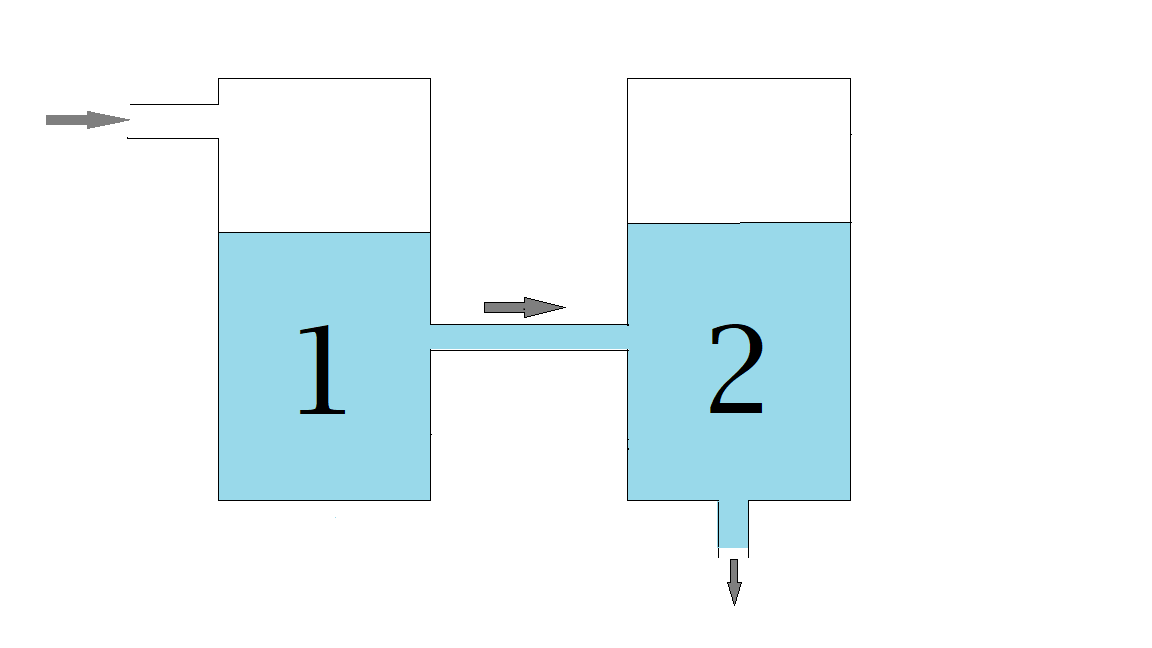
Tank 1 bevat \(200\) gram zout opgelost in \(25\) liter water en tank 2 bevat \(100\) gram zout opgelost in \(20\) liter water.

We nemen aan dat de oplossingen perfect worden gemengd zodat de concentratie zout in elke tank overal gelijk is.

Zoutoplossing met een concentratie van \(10\) gram per liter stroomt in tank 1 met een snelheid van \(5\) liter per minuut.

Vanuit tank 1 stroomt de oplossing naar tank 2 met een snelheid van \(5\) liter per minuut.

Vanuit tank 2 stroomt de oplossing weg met een snelheid van \(5\) liter per minuut.

Merk op dat het volume in elke tank constant blijft. Tegelijkertijd stroomt er \(5\) liter in elke tank en er stroomt \(5\) liter uit.

Stel dat \(x_1(t)\) de hoeveelheid zout (in grammen) in tank 1 op tijdstip \(t\) (in minutes) is en dat \(x_2(t)\) de hoeveelheid zout (in grammen) in tank 2 op tijdstip \(t\) (in minutes) is. Dan geldt

\[x_1'(t)=5\cdot10-5\cdot\frac{x_1(t)}{25}\quad\textrm{en}\quad x_2'(t)=5\cdot\frac{x_1(t)}{25}-5\cdot\frac{x_2(t)}{20},\]

waaruit volgt dat

\[\left\{\begin{array}{l}x_1'(t)=-\displaystyle\frac{1}{5}x_1(t)+50\\[2.5mm] x_2'(t)=\displaystyle\frac{1}{5}x_1(t)-\frac{1}{4}x_2(t)\end{array}\right.\quad\Longleftrightarrow\quad \mathbf{x}'(t)=A\mathbf{x}(t)+\mathbf{g}(t) \quad\textrm{met}\quad A=\begin{pmatrix}-\displaystyle\frac{1}{5}&\displaystyle0\\ \displaystyle\frac{1}{5}&-\displaystyle\frac{1}{4}\end{pmatrix}\quad\textrm{en}\quad\mathbf{g}(t)=\begin{pmatrix}50\\[2.5mm]0\end{pmatrix}.\]

De eigenwaarden van \(A\) zijn \(r_1=-\displaystyle\frac{1}{5}\) en \(r_2=-\displaystyle\frac{1}{4}\) met bijbehorende eigenvectoren \(\mathbf{v}=\begin{pmatrix}1\\4\end{pmatrix}\) en \(\mathbf{v}=\begin{pmatrix}0\\1\end{pmatrix}\) respectievelijk (bijvoorbeeld). Voor een particulier oplossing \(\mathbf{x}_p(t)=\mathbf{p}\) vinden we \(\mathbf{0}=A\mathbf{p}+\mathbf{g}(t)\;\Longleftrightarrow\;-A\mathbf{p}=\mathbf{g}(t)\):

\[\begin{pmatrix}\displaystyle\frac{1}{5}&\displaystyle0\\ -\displaystyle\frac{1}{5}&\displaystyle\frac{1}{4}\end{pmatrix}\mathbf{p}=\begin{pmatrix}50\\[2.5mm]0\end{pmatrix} \quad\Longrightarrow\quad\mathbf{p}=\begin{pmatrix}250\\[2.5mm]200\end{pmatrix}.\]

De algemene oplossing is dus

\[\begin{pmatrix}x_1(t)\\x_2(t)\end{pmatrix}=\mathbf{x}(t)=\mathbf{p}+c_1\mathbf{v}_1e^{r_1t}+c_2\mathbf{v}_2e^{r_2t} =\begin{pmatrix}250\\200\end{pmatrix}+c_1\begin{pmatrix}1\\4\end{pmatrix}e^{-\frac{1}{5}t} +c_2\begin{pmatrix}0\\1\end{pmatrix}e^{-\frac{1}{4}t},\quad c_1,c_2\in\mathbb{R}.\]

Ten slotte gebruiken we de beginvoorwaarden \(x_1(0)=200\) en \(x_2(0)=100\) en vinden dat

\[\begin{pmatrix}200\\100\end{pmatrix}=\begin{pmatrix}250\\200\end{pmatrix}+c_1\begin{pmatrix}1\\4\end{pmatrix} +c_2\begin{pmatrix}0\\1\end{pmatrix}\quad\Longleftrightarrow\quad c_1\begin{pmatrix}1\\4\end{pmatrix} +c_2\begin{pmatrix}0\\1\end{pmatrix}=\begin{pmatrix}-50\\-100\end{pmatrix}\quad\Longleftrightarrow\quad \begin{pmatrix}1&0\\4&1\end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix}=\begin{pmatrix}-50\\-100\end{pmatrix}.\]

Hieruit volgt dat \(c_1=-50\) en \(c_2=100\). De oplossing is dus

\[x_1(t)=250-50e^{-\frac{1}{5}t}\quad\textrm{and}\quad x_2(t)=200-200e^{-\frac{1}{5}t}+100e^{-\frac{1}{4}t}.\]

Merk op dat hieruit volgt dat

\[\lim\limits_{t\to\infty}x_1(t)=250\quad\textrm{en}\quad\lim\limits_{t\to\infty}x_2(t)=200.\]

Als we lang genoeg wachten, dan zal de concentratie zout \(10\) gram per liter zijn in elke tank. Na \(20\) minuten geldt

\[x_1(20)=250-50e^{-4}\approx249\quad\textrm{and}\quad x_2(t)=200-200e^{-4}+100e^{-5}\approx197.\]

Na \(20\) minuten zal tank 1 dus ongeveer \(249\) gram zout en tank 2 ongeveer \(197\) gram zout bevatten. We kunnen ook vragen beantwoorden zoals: "Hoelang duurt het voordat tank 1 \(225\) gram zout bevat?"

\[x_1(t)=225\quad\Longleftrightarrow\quad250-50e^{-\frac{1}{5}t}=225\quad\Longleftrightarrow\quad e^{-\frac{1}{5}t}=\frac{1}{2} \quad\Longleftrightarrow\quad t=-5\ln\left(\frac{1}{2}\right)=5\ln(2).\]

Het duurt dus \(5\ln(2)\approx2.5\) minuten voordat tank 1 \(225\) gram zout bevat. Iets lastiger te beantwoorden is de vraag: "Hoelang duurt het voordat tank 2 \(150\) gram zout bevat?"

\[x_2(t)=150\quad\Longleftrightarrow\quad200-200e^{-\frac{1}{5}t}+100e^{-\frac{1}{4}t}=150\quad\Longleftrightarrow\quad 200e^{-\frac{1}{5}t}-100e^{-\frac{1}{4}t}=50\quad\Longleftrightarrow\quad4e^{-\frac{1}{5}t}-2e^{-\frac{1}{4}t}=1.\]

Nemen we bijvoorbeeld \(e^{-\frac{1}{20}t}=q\) dan volgt dat \(4q^4-2q^5=1\) en dat is niet eenvoudig exact op te lossen. Echter. met behulp van een computer kunnen we wel een numeriek resultaat vinden:

\[e^{-\frac{1}{20}t}=q\approx0.80412\quad\Longrightarrow\quad t=-20\ln(0.80412)\approx4.36.\]

We concluderen dat het ongeveer \(4.36\) minuten duurt voordat tank 2 \(150\) gram zout bevat.

2) Beschouw de onderling gekoppelde vaten getoond in het plaatje:

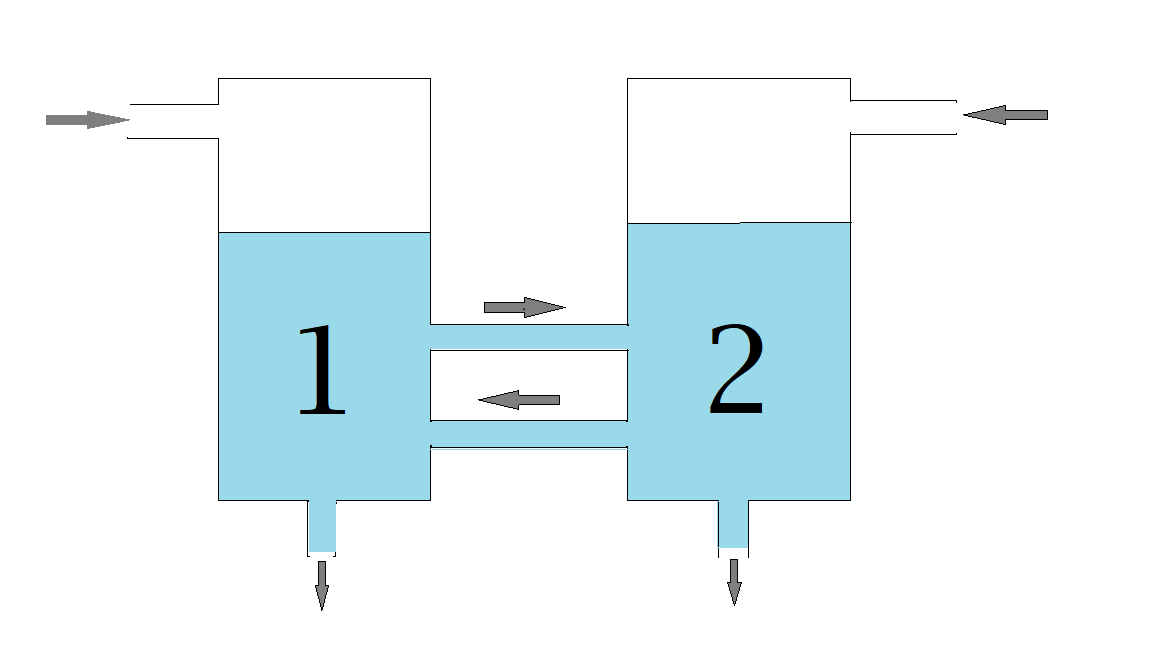
Tank 1 bevat \(200\) gram zout opgelost in \(40\) liter water en tank 2 bevat \(300\) gram zout opgelost in \(60\) liter water.

We nemen aan dat de oplossingen perfect worden gemengd zodat de concentratie zout in elke tank overal gelijk is.

Zoutoplossing met een concentratie van \(5\) gram per liter stroomt in tank 1 met een snelheid van \(4\) liter per minuut en zoutoplossing met een concentratie van \(3\) gram per liter stroomt in tank 2 met een snelheid van \(6\) liter per minuut.

Vanuit tank 1 stroomt de oplossing naar tank 2 met een snelheid van \(3\) liter per minuut en vanuit tank 2 stroomt de oplossing naar tank 1 met een snelheid van \(2\) liter per minuut.

Bovendien stroomt er een deel van de oplossing in tank 1 weg met een snelheid van \(3\) liter per minuut en evenzo stroomt er een deel van de oplossing in tank 2 weg met een snelheid van \(7\) liter per minuut.

Merk op dat het volume in elke tank constant blijft. Tegelijkertijd stroomt er \(4+2=6\) liter in tank 1 en stroomt er \(3+3=6\) liter uit, terwijl er \(6+3=9\) liter in tank 2 stroomt en \(2+7=9\) liter eruit.

Stel dat \(x_1(t)\) de hoeveelheid zout (in grammen) in tank 1 op tijdstip \(t\) (in minutes) is en dat \(x_2(t)\) de hoeveelheid zout (in grammen) in tank 2 op tijdtstip \(t\) (in minutes) is. Dan geldt

\[x_1'(t)=4\cdot5+2\cdot\frac{x_2(t)}{60}-(3+3)\cdot\frac{x_1(t)}{40}\quad\textrm{en}\quad x_2'(t)=6\cdot2+3\cdot\frac{x_1(t)}{40}-(2+7)\cdot\frac{x_2(t)}{60},\]

waaruit volgt dat

\[\left\{\begin{array}{l}x_1'(t)=-\displaystyle\frac{3}{20}x_1(t)+\frac{1}{30}x_2(t)+20\\[2.5mm] x_2'(t)=\displaystyle\frac{3}{40}x_1(t)-\frac{3}{20}x_2(t)+12\end{array}\right.\quad\Longleftrightarrow\quad \mathbf{x}'(t)=A\mathbf{x}(t)+\mathbf{g}(t) \quad\textrm{with}\quad A=\begin{pmatrix}-\displaystyle\frac{3}{20}&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&-\displaystyle\frac{3}{20}\end{pmatrix}\quad\textrm{and}\quad\mathbf{g}(t)=\begin{pmatrix}20\\[2.5mm]12\end{pmatrix}.\]

Nu geldt

\[\left|A-r\,I\right|=\begin{vmatrix}-\displaystyle\frac{3}{20}-r&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&-\displaystyle\frac{3}{20}-r\end{vmatrix}=r^2+\frac{3}{10}r+\frac{1}{50} =\left(r+\frac{1}{5}\right)\left(r+\frac{1}{10}\right)\]

De eigenwaarden zijn dus \(-\dfrac{1}{5}\) en \(-\dfrac{1}{10}\). Voor de eigenvectoren vinden we

\[r_1=-\frac{1}{5}:\quad\begin{pmatrix}-\displaystyle\frac{3}{20}+\frac{1}{5}&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&-\displaystyle\frac{3}{20}+\frac{1}{5}\end{pmatrix}\sim \begin{pmatrix}\displaystyle\frac{1}{20}&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&\displaystyle\frac{1}{20}\end{pmatrix}\sim\begin{pmatrix}3&2\\0&0\end{pmatrix} \quad\Longrightarrow\quad\mathbf{v}_1=\begin{pmatrix}2\\-3\end{pmatrix}\]

en

\[r_2=-\frac{1}{10}:\quad\begin{pmatrix}-\displaystyle\frac{3}{20}+\frac{1}{10}&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&-\displaystyle\frac{3}{20}+\frac{1}{10}\end{pmatrix}\sim \begin{pmatrix}-\displaystyle\frac{1}{20}&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&-\displaystyle\frac{1}{20}\end{pmatrix}\sim\begin{pmatrix}-3&2\\0&0\end{pmatrix} \quad\Longrightarrow\quad\mathbf{v}_2=\begin{pmatrix}2\\3\end{pmatrix}.\]

Voor een particuliere oplossing \(\mathbf{x}_p(t)=\mathbf{p}\) vinden we \(\mathbf{0}=A\mathbf{p}+\mathbf{g}(t)\;\Longleftrightarrow\;-A\mathbf{p}=\mathbf{g}(t)\):

\[\begin{pmatrix}\displaystyle\frac{3}{20}&-\displaystyle\frac{1}{30}\\ -\displaystyle\frac{3}{40}&\displaystyle\frac{3}{20}\end{pmatrix}\mathbf{p}=\begin{pmatrix}20\\[2.5mm]12\end{pmatrix}:\; \left(\left.\begin{matrix}\displaystyle\frac{3}{20}&-\displaystyle\frac{1}{30}\\ -\displaystyle\frac{3}{40}&\displaystyle\frac{3}{20}\end{matrix}\right|\begin{matrix}20\\[2.5mm]12\end{matrix}\right)\sim \left(\left.\begin{matrix}9&-2\\-1&2\end{matrix}\,\right|\,\begin{matrix}1200\\160\end{matrix}\right)\sim \left(\left.\begin{matrix}8&0\\-1&2\end{matrix}\,\right|\,\begin{matrix}1360\\160\end{matrix}\right)\sim \left(\left.\begin{matrix}1&0\\0&2\end{matrix}\,\right|\,\begin{matrix}170\\330\end{matrix}\right) \;\Longrightarrow\;\mathbf{p}=\begin{pmatrix}170\\165\end{pmatrix}.\]

De algemene oplossing is dus

\[\begin{pmatrix}x_1(t)\\x_2(t)\end{pmatrix}=\mathbf{x}(t)=\mathbf{p}+c_1\mathbf{v}_1e^{r_1t}+c_2\mathbf{v}_2e^{r_2t} =\begin{pmatrix}170\\165\end{pmatrix}+c_1\begin{pmatrix}2\\-3\end{pmatrix}e^{-\frac{1}{5}t} +c_2\begin{pmatrix}2\\3\end{pmatrix}e^{-\frac{1}{10}t},\quad c_1,c_2\in\mathbb{R}.\]

Ten slotte gebruiken we de beginvoorwaarden \(x_1(0)=200\) en \(x_2(0)=300\) en vinden dat

\[\begin{pmatrix}200\\300\end{pmatrix}=\begin{pmatrix}170\\165\end{pmatrix}+c_1\begin{pmatrix}2\\-3\end{pmatrix} +c_2\begin{pmatrix}2\\3\end{pmatrix}\quad\Longleftrightarrow\quad c_1\begin{pmatrix}2\\-3\end{pmatrix} +c_2\begin{pmatrix}2\\3\end{pmatrix}=\begin{pmatrix}30\\135\end{pmatrix}\quad\Longleftrightarrow\quad \begin{pmatrix}1&1\\-1&1\end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix}=\begin{pmatrix}15\\45\end{pmatrix}.\]

Hieruit volgt dat \(c_1=-15\) en \(c_2=30\). De oplossing is dus

\[x_1(t)=170-30e^{-\frac{1}{5}t}+60e^{-\frac{1}{10}t}\quad\textrm{en}\quad x_2(t)=165+45e^{-\frac{1}{5}t}+90e^{-\frac{1}{10}t}.\]

Merk op dat hieruit volgt dat

\[\lim\limits_{t\to\infty}x_1(t)=170\quad\textrm{en}\quad\lim\limits_{t\to\infty}x_2(t)=165.\]

Verder volgt bijvoorbeeld dat

\[x_1(10)=170-30e^{-2}+60e^{-1}\approx188.0\quad\textrm{en}\quad x_2(10)=165+45e^{-2}+90e^{-1}\approx204.2,\]

waaruit volgt dat na \(10\) minutes tank 1 ongeveer \(188.0\) gram zout bevat en tank 2 ongeveer \(204.2\) gram zout. Na een half uur (\(30\) minuten) geldt

\[x_1(30)=170-30e^{-6}+60e^{-3}\approx172.9\quad\textrm{en}\quad x_2(30)=165+45e^{-6}+90e^{-3}\approx169.6,\]

waaruit volt dat na een half uur (\(30\) minuten) tank 1 ongeveer \(172.9\) gram zout beavt en tank 2 ongeveer \(169.6\) gram zout. We kunnen nu ook vragen beantwoorden zoals: "Hoelang duurt het voordat tank 1 \(185\) gram zout bevat?"

\[x_1(t)=185\quad\Longleftrightarrow\quad170-30e^{-\frac{1}{5}t}+60e^{-\frac{1}{10}t}=185 \quad\Longleftrightarrow\quad-30e^{-\frac{1}{5}t}+60e^{-\frac{1}{10}t}=15 \quad\Longleftrightarrow\quad-2e^{-\frac{1}{5}t}+4e^{-\frac{1}{10}t}=1.\]

Nemen we \(e^{-\frac{1}{10}t}=q\) dan volgt \(2q^2-4q+1=0\) met oplossingen \(q=1\pm\frac{1}{2}\sqrt{2}\). Dit leidt tot

\[e^{-\frac{1}{10}t}=1\pm\frac{1}{2}\sqrt{2}\quad\Longleftrightarrow\quad t=-10\ln\left(1\pm\frac{1}{2}\sqrt{2}\right).\]

Omdat \(-10\ln\left(1+\frac{1}{2}\sqrt{2}\right)\approx-5.35\) negatief is concluderen we dat het \(-10\ln\left(1-\frac{1}{2}\sqrt{2}\right)\approx12.28\) minuten duurt voordat tank 1 \(185\) gram zout bevat. Evenzo: "Hoelang duurt het voordat tank 2 \(200\) gram zout bevat?"

\[x_2(t)=200\quad\Longleftrightarrow\quad165+45e^{-\frac{1}{5}t}+90e^{-\frac{1}{10}t}=200 \quad\Longleftrightarrow\quad45e^{-\frac{1}{5}t}+90e^{-\frac{1}{10}t}=35 \quad\Longleftrightarrow\quad9e^{-\frac{1}{5}t}+18e^{-\frac{1}{10}t}=7.\]

Nemen we \(e^{-\frac{1}{10}t}=q\) dan volgt \(9q^2+18q-7=0\;\Longleftrightarrow\;(3q-1)(3q+7)=0\). Omdat \(e^{-\frac{1}{10}t}\) positief moet zijn, concluderen we dat

\[e^{-\frac{1}{10}t}=\frac{1}{3}\quad\Longleftrightarrow\quad t=-10\ln\left(\frac{1}{3}\right)=10\ln(3)\approx10.99.\]

Het duurt dus ongeveer \(11\) minuten voordat tank 2 \(200\) gram zout bevat. "Wanneer zal de hoeveelheid zout in beide tanks gelijk zijn?"

\[x_1(t)=x_2(t)\quad\Longleftrightarrow\quad170-30e^{-\frac{1}{5}t}+60e^{-\frac{1}{10}t} =165+45e^{-\frac{1}{5}t}+90e^{-\frac{1}{10}t}\quad\Longleftrightarrow\quad75e^{-\frac{1}{5}t}+30e^{-\frac{1}{10}t}-5=0.\]

Als we weer \(e^{-\frac{1}{10}t}=q\) nemen, dan volgt

\[75q^2+30q-5=0\quad\Longleftrightarrow\quad15q^2+6q-1=0\quad\textrm{met oplossingen}\quad q=\frac{-3\pm2\sqrt{6}}{15}.\]

Omdat \(e^{-\frac{1}{10}t}\) positief moet zijn, concluderen we dat

\[e^{-\frac{1}{10}t}=\frac{-3+2\sqrt{6}}{15}\quad\Longleftrightarrow\quad t=-10\ln\left(\frac{-3+2\sqrt{6}}{15}\right)\approx20.67.\]

Met behulp van een computer zouden we kunnen checken dat na \(\displaystyle-10\ln\left(\frac{-3+2\sqrt{6}}{15}\right)\approx20.67\) minuten geldt

\[x_1\left(-10\ln\left(\frac{-3+2\sqrt{6}}{15}\right)\right)=\frac{768+48\sqrt{6}}{5}=x_2\left(-10\ln\left(\frac{-3+2\sqrt{6}}{15}\right)\right).\]

We concluderen dat na \(\displaystyle-10\ln\left(\frac{-3+2\sqrt{6}}{15}\right)\approx20.67\) minuten beide tanks \(\displaystyle\frac{768+48\sqrt{6}}{5}\approx177.115\) gram zout bevatten.

---

Laatst gewijzigd op 25 oktober 2021