Differential equations – Systems of linear differential equations – Applications
1) Consider the connected tanks shown in the picture:
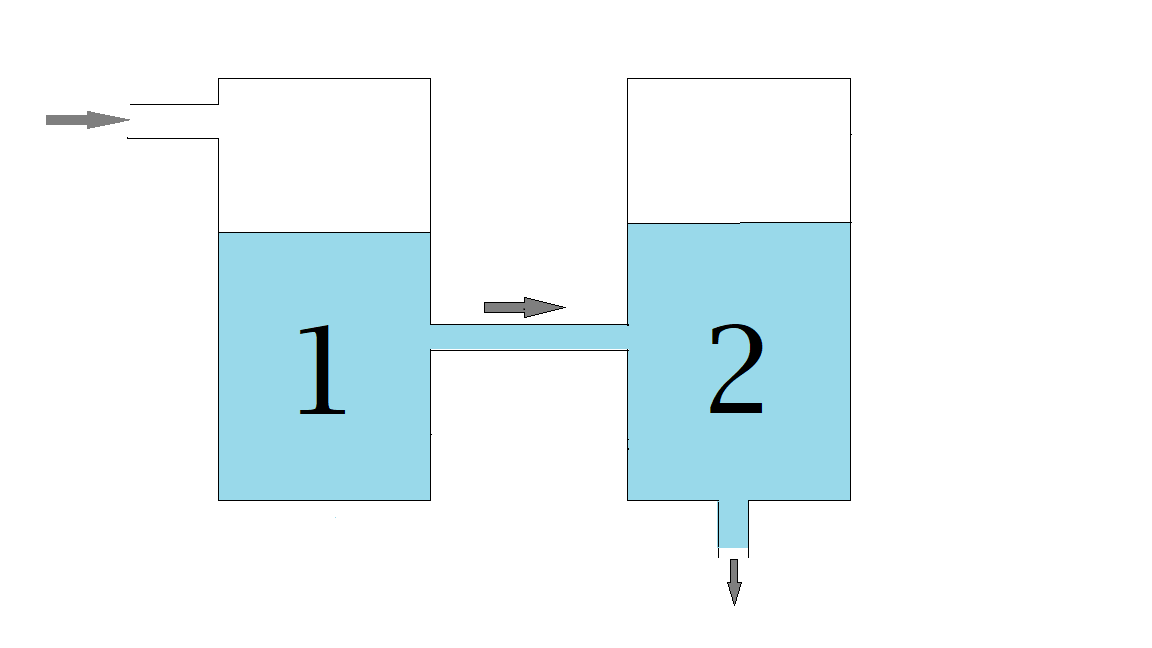
Tank 1 contains \(200\) grams of salt dissolved in \(25\) liters water and tank 2 contains \(100\) grams of salt dissolved in \(20\) liters of water.
We assume that the mixtures are thoroughly mixed such that the concentration in each tank is the same everywhere.
Brine with a concentration of \(10\) grams per liter enters tank 1 at a rate of \(5\) liters per minute.
From tank 1 the mixture flows into tank 2 at a rate of \(5\) liters per minute.
From tank 2 the mixture drains at a rate of \(5\) liters per minute.
Note that the volume in each tank stays constant. Simultaneously \(5\) liters enter each tank and \(5\) liters drain from it.
Let \(x_1(t)\) denote the amount of salt (in grams) in tank 1 at time \(t\) (in minutes) and let \(x_2(t)\) denote the amount of salt (in grams) in tank 2 at time \(t\) (in minutes). Then we have
\[x_1'(t)=5\cdot10-5\cdot\frac{x_1(t)}{25}\quad\textrm{and}\quad x_2'(t)=5\cdot\frac{x_1(t)}{25}-5\cdot\frac{x_2(t)}{20},\]which implies that
\[\left\{\begin{array}{l}x_1'(t)=-\displaystyle\frac{1}{5}x_1(t)+50\\[2.5mm] x_2'(t)=\displaystyle\frac{1}{5}x_1(t)-\frac{1}{4}x_2(t)\end{array}\right.\quad\Longleftrightarrow\quad \mathbf{x}'(t)=A\mathbf{x}(t)+\mathbf{g}(t) \quad\textrm{with}\quad A=\begin{pmatrix}-\displaystyle\frac{1}{5}&\displaystyle0\\ \displaystyle\frac{1}{5}&-\displaystyle\frac{1}{4}\end{pmatrix}\quad\textrm{and}\quad\mathbf{g}(t)=\begin{pmatrix}50\\[2.5mm]0\end{pmatrix}.\]The eigenvalues of \(A\) are \(r_1=-\displaystyle\frac{1}{5}\) and \(r_2=-\displaystyle\frac{1}{4}\) with corresponding eigenvectors \(\mathbf{v}=\begin{pmatrix}1\\4\end{pmatrix}\) and \(\mathbf{v}=\begin{pmatrix}0\\1\end{pmatrix}\) respectively (for instance). For a particular solution \(\mathbf{x}_p(t)=\mathbf{p}\) we obtain \(\mathbf{0}=A\mathbf{p}+\mathbf{g}(t)\;\Longleftrightarrow\;-A\mathbf{p}=\mathbf{g}(t)\):
\[\begin{pmatrix}\displaystyle\frac{1}{5}&\displaystyle0\\ -\displaystyle\frac{1}{5}&\displaystyle\frac{1}{4}\end{pmatrix}\mathbf{p}=\begin{pmatrix}50\\[2.5mm]0\end{pmatrix} \quad\Longrightarrow\quad\mathbf{p}=\begin{pmatrix}250\\[2.5mm]200\end{pmatrix}.\]So the general solution is
\[\begin{pmatrix}x_1(t)\\x_2(t)\end{pmatrix}=\mathbf{x}(t)=\mathbf{p}+c_1\mathbf{v}_1e^{r_1t}+c_2\mathbf{v}_2e^{r_2t} =\begin{pmatrix}250\\200\end{pmatrix}+c_1\begin{pmatrix}1\\4\end{pmatrix}e^{-\frac{1}{5}t} +c_2\begin{pmatrix}0\\1\end{pmatrix}e^{-\frac{1}{4}t},\quad c_1,c_2\in\mathbb{R}.\]Finally, we use the initial values \(x_1(0)=200\) and \(x_2(0)=100\) to find that
\[\begin{pmatrix}200\\100\end{pmatrix}=\begin{pmatrix}250\\200\end{pmatrix}+c_1\begin{pmatrix}1\\4\end{pmatrix} +c_2\begin{pmatrix}0\\1\end{pmatrix}\quad\Longleftrightarrow\quad c_1\begin{pmatrix}1\\4\end{pmatrix} +c_2\begin{pmatrix}0\\1\end{pmatrix}=\begin{pmatrix}-50\\-100\end{pmatrix}\quad\Longleftrightarrow\quad \begin{pmatrix}1&0\\4&1\end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix}=\begin{pmatrix}-50\\-100\end{pmatrix}.\]This implies that \(c_1=-50\) and \(c_2=100\). Hence the solution is
\[x_1(t)=250-50e^{-\frac{1}{5}t}\quad\textrm{and}\quad x_2(t)=200-200e^{-\frac{1}{5}t}+100e^{-\frac{1}{4}t}.\]Note that this implies that
\[\lim\limits_{t\to\infty}x_1(t)=250\quad\textrm{and}\quad\lim\limits_{t\to\infty}x_2(t)=200.\]If we wait long enough, the concentration of salt will be \(10\) grams per liter in each tank. After \(20\) minutes we have
\[x_1(20)=250-50e^{-4}\approx249\quad\textrm{and}\quad x_2(t)=200-200e^{-4}+100e^{-5}\approx197.\]So after \(20\) minutes tank 1 will contain approximately \(249\) grams of salt and tank 2 will contain approximately \(197\) grams of salt. We can also answer questions like: "How long does it take for tank 1 to contain \(225\) grams of salt?"
\[x_1(t)=225\quad\Longleftrightarrow\quad250-50e^{-\frac{1}{5}t}=225\quad\Longleftrightarrow\quad e^{-\frac{1}{5}t}=\frac{1}{2} \quad\Longleftrightarrow\quad t=-5\ln\left(\frac{1}{2}\right)=5\ln(2).\]Hence it takes \(5\ln(2)\approx2.5\) minutes for tank 1 to contain \(225\) grams of salt. Somewhat more difficult is to answer the question: "How long does it take for tank 2 to contain \(150\) grams of salt?"
\[x_2(t)=150\quad\Longleftrightarrow\quad200-200e^{-\frac{1}{5}t}+100e^{-\frac{1}{4}t}=150\quad\Longleftrightarrow\quad 200e^{-\frac{1}{5}t}-100e^{-\frac{1}{4}t}=50\quad\Longleftrightarrow\quad4e^{-\frac{1}{5}t}-2e^{-\frac{1}{4}t}=1.\]Taking for instance \(e^{-\frac{1}{20}t}=q\) this implies that \(4q^4-2q^5=1\) which is not easy to solve exactly. However, using a computer we can find a numerical result:
\[e^{-\frac{1}{20}t}=q\approx0.80412\quad\Longrightarrow\quad t=-20\ln(0.80412)\approx4.36.\]We conclude that it takes approximately \(4.36\) minutes for tank 2 to contain \(150\) grams of salt.
2) Consider the interconnected tanks shown in the picture:
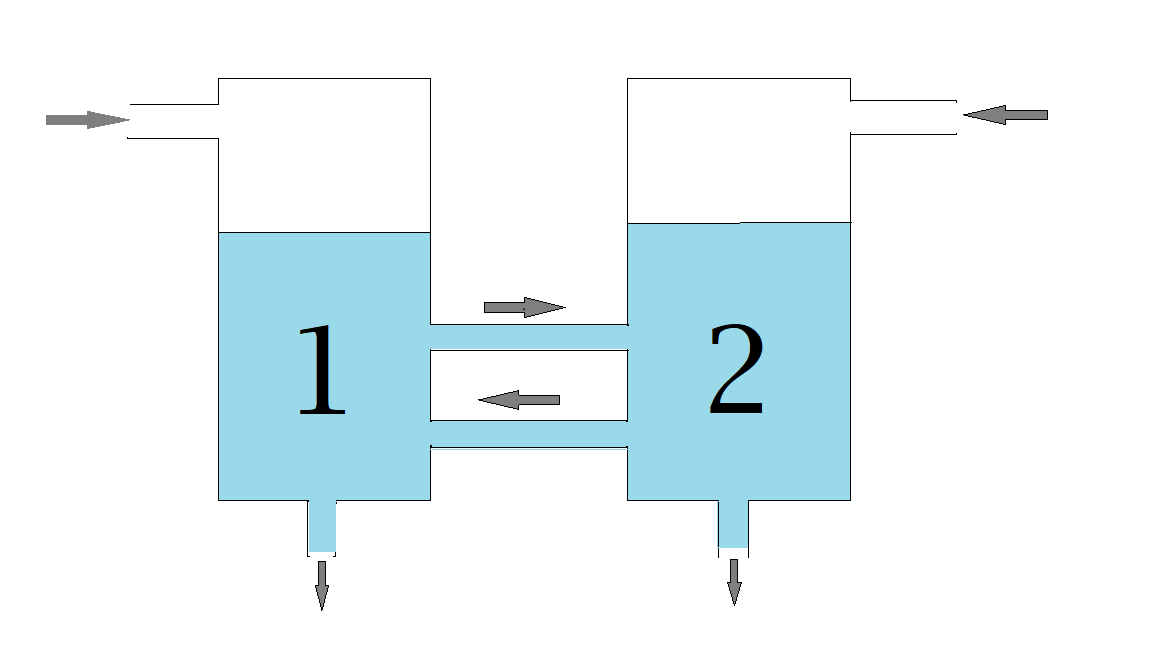
Tank 1 contains \(200\) grams of salt dissolved in \(40\) liters water and tank 2 contains \(300\) grams of salt dissolved in \(60\) liters of water.
We assume that the mixtures are thoroughly mixed such that the concentration in each tank is the same everywhere
Brine with a concentration of \(5\) grams per liter enters tank 1 at a rate of \(4\) liters per minute and brine with a concentration of \(3\) grams per liters enters tank 2 at a rate of \(6\) liters per minute.
From tank 1 the mixture flows into tank 2 at a rate of \(3\) liters per minute and from tank 2 the mixture flows into tank 1 at a rate of \(2\) liters per minute.
Moreover a part of the mixture in tank 1 drains at a rate of \(3\) liters per minute and likewise a part of the mixture in tank 2 drains at a rate of \(7\) liters per minute.
Note that the volume in each tank stays constant. Simultaneously, \(4+2=6\) liters enters tank 1 and \(3+3=6\) drains from it, while \(6+3=9\) liters enters tank 2 and \(2+7=9\) liters drains from it.
Let \(x_1(t)\) denote the amount of salt (in grams) in tank 1 at time \(t\) (in minutes) and let \(x_2(t)\) denote the amount of salt (in grams) in tank 2 at time \(t\) (in minutes). Then we have
\[x_1'(t)=4\cdot5+2\cdot\frac{x_2(t)}{60}-(3+3)\cdot\frac{x_1(t)}{40}\quad\textrm{and}\quad x_2'(t)=6\cdot2+3\cdot\frac{x_1(t)}{40}-(2+7)\cdot\frac{x_2(t)}{60},\]which implies that
\[\left\{\begin{array}{l}x_1'(t)=-\displaystyle\frac{3}{20}x_1(t)+\frac{1}{30}x_2(t)+20\\[2.5mm] x_2'(t)=\displaystyle\frac{3}{40}x_1(t)-\frac{3}{20}x_2(t)+12\end{array}\right.\quad\Longleftrightarrow\quad \mathbf{x}'(t)=A\mathbf{x}(t)+\mathbf{g}(t) \quad\textrm{with}\quad A=\begin{pmatrix}-\displaystyle\frac{3}{20}&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&-\displaystyle\frac{3}{20}\end{pmatrix}\quad\textrm{and}\quad\mathbf{g}(t)=\begin{pmatrix}20\\[2.5mm]12\end{pmatrix}.\]Now we have
\[\left|A-r\,I\right|=\begin{vmatrix}-\displaystyle\frac{3}{20}-r&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&-\displaystyle\frac{3}{20}-r\end{vmatrix}=r^2+\frac{3}{10}r+\frac{1}{50} =\left(r+\frac{1}{5}\right)\left(r+\frac{1}{10}\right)\]So the eigenvalues are \(-\dfrac{1}{5}\) and \(-\dfrac{1}{10}\). For the eigenvectors we obtain
\[r_1=-\frac{1}{5}:\quad\begin{pmatrix}-\displaystyle\frac{3}{20}+\frac{1}{5}&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&-\displaystyle\frac{3}{20}+\frac{1}{5}\end{pmatrix}\sim \begin{pmatrix}\displaystyle\frac{1}{20}&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&\displaystyle\frac{1}{20}\end{pmatrix}\sim\begin{pmatrix}3&2\\0&0\end{pmatrix} \quad\Longrightarrow\quad\mathbf{v}_1=\begin{pmatrix}2\\-3\end{pmatrix}\]and
\[r_2=-\frac{1}{10}:\quad\begin{pmatrix}-\displaystyle\frac{3}{20}+\frac{1}{10}&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&-\displaystyle\frac{3}{20}+\frac{1}{10}\end{pmatrix}\sim \begin{pmatrix}-\displaystyle\frac{1}{20}&\displaystyle\frac{1}{30}\\ \displaystyle\frac{3}{40}&-\displaystyle\frac{1}{20}\end{pmatrix}\sim\begin{pmatrix}-3&2\\0&0\end{pmatrix} \quad\Longrightarrow\quad\mathbf{v}_2=\begin{pmatrix}2\\3\end{pmatrix}.\]For a particular solution \(\mathbf{x}_p(t)=\mathbf{p}\) we obtain \(\mathbf{0}=A\mathbf{p}+\mathbf{g}(t)\;\Longleftrightarrow\;-A\mathbf{p}=\mathbf{g}(t)\):
\[\begin{pmatrix}\displaystyle\frac{3}{20}&-\displaystyle\frac{1}{30}\\ -\displaystyle\frac{3}{40}&\displaystyle\frac{3}{20}\end{pmatrix}\mathbf{p}=\begin{pmatrix}20\\[2.5mm]12\end{pmatrix}:\; \left(\left.\begin{matrix}\displaystyle\frac{3}{20}&-\displaystyle\frac{1}{30}\\ -\displaystyle\frac{3}{40}&\displaystyle\frac{3}{20}\end{matrix}\right|\begin{matrix}20\\[2.5mm]12\end{matrix}\right)\sim \left(\left.\begin{matrix}9&-2\\-1&2\end{matrix}\,\right|\,\begin{matrix}1200\\160\end{matrix}\right)\sim \left(\left.\begin{matrix}8&0\\-1&2\end{matrix}\,\right|\,\begin{matrix}1360\\160\end{matrix}\right)\sim \left(\left.\begin{matrix}1&0\\0&2\end{matrix}\,\right|\,\begin{matrix}170\\330\end{matrix}\right) \;\Longrightarrow\;\mathbf{p}=\begin{pmatrix}170\\165\end{pmatrix}.\]So the general solution is
\[\begin{pmatrix}x_1(t)\\x_2(t)\end{pmatrix}=\mathbf{x}(t)=\mathbf{p}+c_1\mathbf{v}_1e^{r_1t}+c_2\mathbf{v}_2e^{r_2t} =\begin{pmatrix}170\\165\end{pmatrix}+c_1\begin{pmatrix}2\\-3\end{pmatrix}e^{-\frac{1}{5}t} +c_2\begin{pmatrix}2\\3\end{pmatrix}e^{-\frac{1}{10}t},\quad c_1,c_2\in\mathbb{R}.\]Finally, we use the initial values \(x_1(0)=200\) and \(x_2(0)=300\) to find that
\[\begin{pmatrix}200\\300\end{pmatrix}=\begin{pmatrix}170\\165\end{pmatrix}+c_1\begin{pmatrix}2\\-3\end{pmatrix} +c_2\begin{pmatrix}2\\3\end{pmatrix}\quad\Longleftrightarrow\quad c_1\begin{pmatrix}2\\-3\end{pmatrix} +c_2\begin{pmatrix}2\\3\end{pmatrix}=\begin{pmatrix}30\\135\end{pmatrix}\quad\Longleftrightarrow\quad \begin{pmatrix}1&1\\-1&1\end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix}=\begin{pmatrix}15\\45\end{pmatrix}.\]This implies that \(c_1=-15\) and \(c_2=30\). Hence the solution is
\[x_1(t)=170-30e^{-\frac{1}{5}t}+60e^{-\frac{1}{10}t}\quad\textrm{and}\quad x_2(t)=165+45e^{-\frac{1}{5}t}+90e^{-\frac{1}{10}t}.\]Note that this implies that
\[\lim\limits_{t\to\infty}x_1(t)=170\quad\textrm{and}\quad\lim\limits_{t\to\infty}x_2(t)=165.\]Further we obtain for instance that
\[x_1(10)=170-30e^{-2}+60e^{-1}\approx188.0\quad\textrm{and}\quad x_2(10)=165+45e^{-2}+90e^{-1}\approx204.2,\]which implies that after \(10\) minutes tank 1 contains approximately \(188.0\) grams of salt and tank 2 contains approximately \(204.2\) grams of salt. After half an hour (\(30\) minutes) we have
\[x_1(30)=170-30e^{-6}+60e^{-3}\approx172.9\quad\textrm{and}\quad x_2(30)=165+45e^{-6}+90e^{-3}\approx169.6,\]which implies that after half an hour (\(30\) minutes) tank 1 contains approximately \(172.9\) grams of salt and tank 2 contains approximately \(169.6\) grams of salt. We can also answer questions like: "How long does it take for tank 1 to contain \(185\) grams of salt?"
\[x_1(t)=185\quad\Longleftrightarrow\quad170-30e^{-\frac{1}{5}t}+60e^{-\frac{1}{10}t}=185 \quad\Longleftrightarrow\quad-30e^{-\frac{1}{5}t}+60e^{-\frac{1}{10}t}=15 \quad\Longleftrightarrow\quad-2e^{-\frac{1}{5}t}+4e^{-\frac{1}{10}t}=1.\]Taking \(e^{-\frac{1}{10}t}=q\) we obtain \(2q^2-4q+1=0\) with solutions \(q=1\pm\frac{1}{2}\sqrt{2}\). This leads to
\[e^{-\frac{1}{10}t}=1\pm\frac{1}{2}\sqrt{2}\quad\Longleftrightarrow\quad t=-10\ln\left(1\pm\frac{1}{2}\sqrt{2}\right).\]Since \(-10\ln\left(1+\frac{1}{2}\sqrt{2}\right)\approx-5.35\) is negative we conclude that it takes \(-10\ln\left(1-\frac{1}{2}\sqrt{2}\right)\approx12.28\) minutes for tank 1 to contain \(185\) grams of salt. Similarly: "How long does it take for tank 2 to contain \(200\) grams of salt?"
\[x_2(t)=200\quad\Longleftrightarrow\quad165+45e^{-\frac{1}{5}t}+90e^{-\frac{1}{10}t}=200 \quad\Longleftrightarrow\quad45e^{-\frac{1}{5}t}+90e^{-\frac{1}{10}t}=35 \quad\Longleftrightarrow\quad9e^{-\frac{1}{5}t}+18e^{-\frac{1}{10}t}=7.\]Taking \(e^{-\frac{1}{10}t}=q\) we obtain \(9q^2+18q-7=0\;\Longleftrightarrow\;(3q-1)(3q+7)=0\). Since \(e^{-\frac{1}{10}t}\) should be positive, we conclude that
\[e^{-\frac{1}{10}t}=\frac{1}{3}\quad\Longleftrightarrow\quad t=-10\ln\left(\frac{1}{3}\right)=10\ln(3)\approx10.99.\]So it takes approximately \(11\) minutes for tank 2 to contain \(200\) grams of salt. "When will the amount of salt in both tanks be equal?"
\[x_1(t)=x_2(t)\quad\Longleftrightarrow\quad170-30e^{-\frac{1}{5}t}+60e^{-\frac{1}{10}t} =165+45e^{-\frac{1}{5}t}+90e^{-\frac{1}{10}t}\quad\Longleftrightarrow\quad75e^{-\frac{1}{5}t}+30e^{-\frac{1}{10}t}-5=0.\]Again taking \(e^{-\frac{1}{10}t}=q\) we obtain
\[75q^2+30q-5=0\quad\Longleftrightarrow\quad15q^2+6q-1=0\quad\textrm{with solutions}\quad q=\frac{-3\pm2\sqrt{6}}{15}.\]Since \(e^{-\frac{1}{10}t}\) should be positive, we conclude that
\[e^{-\frac{1}{10}t}=\frac{-3+2\sqrt{6}}{15}\quad\Longleftrightarrow\quad t=-10\ln\left(\frac{-3+2\sqrt{6}}{15}\right)\approx20.67.\]Using a computer we might check that after \(\displaystyle-10\ln\left(\frac{-3+2\sqrt{6}}{15}\right)\approx20.67\) minutes we have
\[x_1\left(-10\ln\left(\frac{-3+2\sqrt{6}}{15}\right)\right)=\frac{768+48\sqrt{6}}{5}=x_2\left(-10\ln\left(\frac{-3+2\sqrt{6}}{15}\right)\right).\]We conclude that after \(\displaystyle-10\ln\left(\frac{-3+2\sqrt{6}}{15}\right)\approx20.67\) minutes both tanks contain \(\displaystyle\frac{768+48\sqrt{6}}{5}\approx177.115\) grams of salt.
Last modified on October 25, 2021
 Teaching
Teaching

