Differentiaalvergelijkingen – Partiële differentiaalvergelijkingen – Voorbeelden

1) \(f(x)=\left\{\begin{array}{ll}0,&-\pi\leq x < 0\\[2.5mm]1,&0\leq x < \pi\end{array}\right.\) en \(f(x+2\pi)=f(x)\).

\(L=\pi\) en \(a_0=\displaystyle\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\,dx=\frac{1}{\pi}\int_0^{\pi}dx=1\). Verder volgt:

\[a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(nx)\,dx=\frac{1}{\pi}\int_0^{\pi}\cos(nx)\,dx=\frac{1}{n\pi}\sin(nx)\bigg|_0^{\pi}=0,\quad n=1,2,3,\ldots\]

en

\[b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(nx)\,dx=\frac{1}{\pi}\int_0^{\pi}\sin(nx)\,dx=-\frac{1}{n\pi}\cos(nx)\bigg|_0^{\pi} =\frac{1-\cos(n\pi)}{n\pi}=\frac{1-(-1)^n}{n\pi},\quad n=1,2,3,\ldots.\]

Merk op dat \(b_{2k}=0\) en \(b_{2k-1}=\displaystyle\frac{2}{(2k-1)\pi}\) voor \(k=1,2,3,\ldots\). Dan volgt dat

\[f(x)=\frac{1}{2}+\sum_{n=1}^{\infty}\frac{1-(-1)^n}{n\pi}\sin(nx)=\frac{1}{2}+\frac{2}{\pi}\sum_{k=1}^{\infty}\frac{\sin(2k-1)x}{2k-1}.\]

Een plot van enkele partiële sommen van deze reeks:

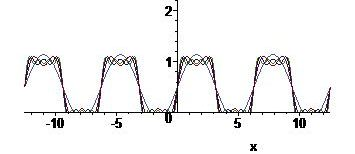
Dit is een voorbeeld van een blokgolf. Rondom de sprongpunten is het verschijnsel van Gibbs zichtbaar.

Voor \(x=\frac{1}{2}\pi\) vinden we met de stelling van Fourier:

\[1=\frac{1}{2}+\frac{2}{\pi}\sum_{k=1}^{\infty}\frac{\sin(k-\frac{1}{2})\pi}{2k-1}\quad\Longleftrightarrow\quad \frac{1}{2}=\frac{2}{\pi}\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{2k-1}\quad\Longleftrightarrow\quad \sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{2k-1}=\frac{1}{4}\pi.\]

Uit de relatie van Parseval volgt:

\[\frac{1}{2}+\frac{4}{\pi^2}\sum_{k=1}^{\infty}\frac{1}{(2k-1)^2}=\frac{1}{\pi}\int_{-\pi}^{\pi}\{f(x)\}^2\,dx=\frac{1}{\pi}\int_0^{\pi}dx=1 \quad\Longrightarrow\quad\sum_{k=1}^{\infty}\frac{1}{(2k-1)^2}=\frac{1}{8}\pi^2.\]

2) \(f(x)=2x\) voor \(-1\leq x\leq 1\) en \(f(x+2)=f(x)\).

\(L=1\) en \(f\) is oneven, dus: \(a_n=0\) voor \(n=0,1,2,\ldots\) en

\begin{align*} b_n&=\frac{1}{1}\int_{-1}^1f(x)\sin(n\pi x)\,dx=\int_{-1}^12x\sin(n\pi x)\,dx=-\frac{1}{n\pi}\int_{-1}^12x\,d\cos(n\pi x)\\[2.5mm] &=-\frac{2x\cos(n\pi x)}{n\pi}\bigg|_{-1}^1+\frac{2}{n\pi}\int_{-1}^1\cos(n\pi x)\,dx =-\frac{4\cos(n\pi)}{n\pi}=\frac{4(-1)^{n+1}}{n\pi},\quad n=1,2,3,\ldots. \end{align*}

Dus: \(f(x)=\displaystyle\frac{4}{\pi}\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}\sin(n\pi x)\).

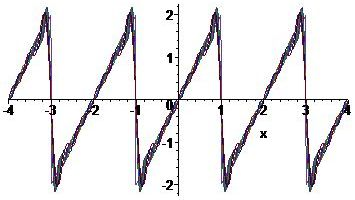
Dit is een voorbeeld van een zaagtandgolf. Rondom de sprongpunten is het verschijnsel van Gibbs zichtbaar.

Voor \(x=\frac{1}{2}\pi\) vinden we met de stelling van Fourier:

\[1=\frac{4}{\pi}\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}\sin\left(\frac{n\pi}{2}\right)=\frac{4}{\pi}\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{2k-1} \quad\Longrightarrow\quad\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{2k-1}=\frac{1}{4}\pi.\]

Uit de relatie van Parseval volgt:

\[\frac{16}{\pi^2}\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{1}{1}\int_{-1}^1\{f(x)\}^2\,dx=\int_{-1}^14x^2\,dx=\frac{4}{3}x^3\bigg|_{-1}^1=\frac{8}{3} \quad\Longrightarrow\quad\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{1}{6}\pi^2.\]

3) \(f(x)=1-x^2\) voor \(-1\leq x\leq 1\) en \(f(x+2)=f(x)\).

\(L=1\) en \(f\) is even, dus: \(b_n=0\) voor \(n=1,2,3,\ldots\). Verder geldt: \(a_0=\displaystyle\frac{1}{1}\int_{-1}^1f(x)\,dx =\int_{_1}^1(1-x^2)\,dx=\left[x-\frac{1}{3}x^3\right]_{-1}^1=\frac{4}{3}\) en

\begin{align*} a_n&=\frac{1}{1}\int_{-1}^1f(x)\cos(n\pi x)\,dx=\int_{-1}^1(1-x^2)\cos(n\pi x)\,dx=\frac{1}{n\pi}\int_{-1}^1(1-x^2)\,d\sin(n\pi x)\\[2.5mm] &=\frac{(1-x^2)\sin(n\pi x)}{n\pi}\bigg|_{-1}^1+\frac{1}{n\pi}\int_{-1}^12x\sin(n\pi x)\,dx =-\frac{1)}{n^2\pi^2}\int_{-1}^12x\,d\cos(n\pi x)\\[2.5mm] &=-\frac{2x\cos(n\pi x)}{n^2\pi^2}+\frac{2}{n^2\pi^2}\int_{-1}^1\cos(n\pi x)\,dx =-\frac{4\cos(n\pi)}{n^2\pi^2}=\frac{4(-1)^{n+1}}{n^2\pi^2},\quad n=1,2,3,\ldots. \end{align*}

Dus: \(f(x)=\displaystyle\frac{2}{3}+\frac{4}{\pi^2}\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n^2}\cos(n\pi x)\).

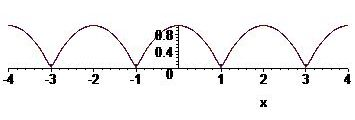
Omdat \(f\) continu is, treedt het verschijnsel van Gibbs hier niet op.

Voor \(x=0\) volgt uit de stelling van Fourier:

\[1=\frac{2}{3}+\frac{4}{\pi^2}\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n^2}\quad\Longrightarrow\quad\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n^2}=\frac{1}{12}\pi^2.\]

Voor \(x=1\) volgt uit de stelling van Fourier:

\[0=\frac{2}{3}+\frac{4}{\pi^2}\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n^2}(-1)^n\quad\Longrightarrow\quad\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{1}{6}\pi^2.\]

Uit de relatie van Parseval volgt:

\[\frac{8}{9}+\frac{16}{\pi^4}\sum_{n=1}^{\infty}\frac{1}{n^4}=\frac{1}{1}\int_{-1}^1\{f(x)\}^2\,dx=\int_{-1}^1(1-x^2)^2\,dx =\int_{-1}^1(1-2x^2+x^4)\,dx=\left[x-\frac{2}{3}x^3+\frac{1}{5}x^5\right]_{-1}^1=\frac{16}{15}\]

oftewel

\[\frac{16}{\pi^4}\sum_{n=1}^{\infty}\frac{1}{n^4}=\frac{16}{15}-\frac{8}{9}=\frac{8}{45}\quad\Longrightarrow\quad \sum_{n=1}^{\infty}\frac{1}{n^4}=\frac{1}{90}\pi^4.\]

4) \(f(x)=x\) voor \(0\leq x\leq 1\).

Als we \(f\) oneven en periodiek voortzetten, dan volgt: \(L=1\) en

\begin{align*} b_n&=\frac{2}{1}\int_0^1f(x)\sin(n\pi x)\,dx=2\int_0^1x\sin(n\pi x)\,dx=-\frac{2}{n\pi}\int_0^1x\,d\cos(n\pi x)\\[2.5mm] &=-\frac{2x\cos(n\pi x)}{n\pi}\bigg|_0^1+\frac{2}{n\pi}\int_0^1\cos(n\pi x)\,dx=-\frac{2\cos(n\pi)}{n\pi}=\frac{2(-1)^{n+1}}{n\pi}, \quad n=1,2,3,\ldots \end{align*}

en dus: \(f(x)=\displaystyle\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}\sin(n\pi x)\).

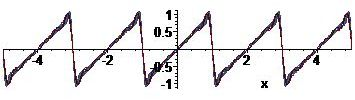
Dit is een voorbeeld van een zaagtandgolf. Rondom de sprongpunten is het verschijnsel van Gibbs zichtbaar.

Als we \(f\) even en periodiek voortzetten, dan volgt: \(L=1\), \(a_0=\displaystyle\frac{2}{1}\int_0^1f(x)\,dx=2\int_0^1x\,dx=x^2\bigg|_0^1=1\) en

\begin{align*} a_n&=\frac{2}{1}\int_0^1f(x)\cos(n\pi x)\,dx=2\int_0^1x\cos(n\pi x)\,dx=\frac{2}{n\pi}\int_0^1x\,d\sin(n\pi x)\\[2.5mm] &=\frac{2x\sin(n\pi x)}{n\pi}\bigg|_0^1-\frac{2}{n\pi}\int_0^1\sin(n\pi x)\,dx=\frac{2}{n^2\pi^2}\cos(n\pi x)\bigg|_0^1 =\frac{2\left((-1)^{n}-1\right)}{n^2\pi^2},\quad n=1,2,3,\ldots \end{align*}

en dus: \(f(x)=\displaystyle\frac{1}{2}+\frac{2}{\pi^2}\sum_{n=1}^{\infty}\frac{(-1)^n-1}{n^2}\cos(n\pi x)\).

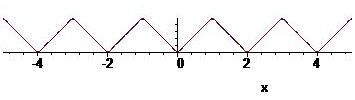
Dit is een voorbeeld van een driehoeksgolf. In dit laatste geval is de functie continu en treedt het verschijnsel van Gibbs niet op.

Voor \(x=1\) volgt uit de stelling van Fourier:

\[1=\frac{1}{2}+\frac{2}{\pi^2}\sum_{n=1}^{\infty}\frac{(-1)^n-1}{n^2}(-1)^n=\frac{1}{2}+\frac{4}{\pi^2}\sum_{k=1}^{\infty}\frac{1}{(2k-1)^2} \quad\Longrightarrow\quad\sum_{k=1}^{\infty}\frac{1}{(2k-1)^2}=\frac{1}{8}\pi^2.\]

Uit de relatie van Parseval volgt:

\[\frac{1}{2}+\frac{16}{\pi^4}\sum_{k=1}^{\infty}\frac{1}{(2k-1)^4}=\frac{1}{1}\int_{-1}^1\{f(x)\}^2\,dx=\int_{-1}^1x^2\,dx =\frac{1}{3}x^3\bigg|_{-1}^1=\frac{2}{3}\]

oftewel

\[\frac{16}{\pi^4}\sum_{n=1}^{\infty}\frac{1}{(2k-1)^4}=\frac{2}{3}-\frac{1}{2}=\frac{1}{6}\quad\Longrightarrow\quad \sum_{n=1}^{\infty}\frac{1}{(2k-1)^4}=\frac{1}{96}\pi^4.\]

---

Laatst gewijzigd op 23 augustus 2021