Special Functions – Orthogonal polynomials – Chebyshev polynomials

For \(x\in[-1,1]\) the Chebyshev polynomials \(T_n(x)\) of the first kind and the Chebyshev polynomials \(U_n(x)\) of the second kind can be defined by

\[T_n(x)=\cos(n\theta)\quad\text{and}\quad U_n(x)=\frac{\sin(n+1)\theta}{\sin\theta},\quad x=\cos\theta,\quad n=0,1,2,\ldots.\]

The orthogonality property is given by

\[\int_{-1}^1(1-x^2)^{-1/2}T_m(x)T_n(x)\,dx=\int_0^{\pi}\cos(m\theta)\,\cos(n\theta)\,d\theta=0,\quad m\ne n\]

and

\[\int_{-1}^1(1-x^2)^{1/2}U_m(x)U_n(x)\,dx=\int_0^{\pi}\sin(m+1)\theta\,\sin(n+1)\theta\,d\theta=0,\quad m\ne n.\]

So the Chebyshev polynomials are special cases of the Jacobi polynomials: \(\alpha=\beta=-\frac{1}{2}\) for the first kind and \(\alpha=\beta=\frac{1}{2}\) for the second kind.

Both families of orthogonal polynomials satisfy the three-term recurrence relation

\[P_{n+1}(x)=2xP_n(x)-P_{n-1}(x),\quad n=1,2,3,\ldots,\]

since we have

\[T_{n+1}(x)+T_{n-1}(x)=\cos(n+1)\theta+\cos(n-1)\theta=2\cos\theta\cos(n\theta)=2xT_n(x)\]

and

\[U_{n+1}(x)+U_{n-1}(x)=\frac{\sin(n+2)\theta+\sin(n\theta)}{\sin\theta}=\frac{2\,\cos\theta\,\sin(n+1)\theta}{\sin\theta}=2xU_n(x).\]

Note that

\[T_0(x)=U_0(x)=1,\quad T_1(x)=x\quad\text{and}\quad U_1(x)=2x.\]

We also have

\[T_n(x)=U_n(x)-xU_{n-1}(x),\quad n=1,2,3,\ldots,\]

since

\[U_n(x)-xU_{n-1}(x)=\frac{\sin(n+1)\theta-\cos\theta\,\sin(n\theta)}{\sin\theta}=\frac{\sin\theta\,\cos(n\theta)}{\sin\theta}=\cos(n\theta)=T_n(x).\]

In order to find a generating function for the Chebyshev polynomials \(T_n(x)\) of the first kind, we multiply the recurrence relation by \(t^{n+1}\) and take the sum to obtain

\[\sum_{n=1}^{\infty}T_{n+1}(x)t^{n+1}=2x\sum_{n=1}^{\infty}T_n(x)t^{n+1}-\sum_{n=1}^{\infty}T_{n-1}(x)t^{n+1}.\]

If we define

\[F(x,t)=\sum_{n=0}^{\infty}T_n(x)t^n,\quad |t|<1,\]

then we have

\[F(x,t)-T_1(x)t-T_0(x)=2xt\left[F(x,t)-T_0(x)\right]-t^2F(x,t).\]

This implies that

\[(1-2xt+t^2)F(x,t)=T_0(x)+T_1(x)t-2xtT_0(x)=1+xt-2xt=1-xt.\]

Hence we have the generating function

\[\sum_{n=0}^{\infty}T_n(x)t^n=F(x,t)=\frac{1-xt}{1-2xt+t^2},\quad |t|<1.\]

In the same way we have for the Chebyshev polynomials \(U_n(x)\) of the second kind:

\[G(x,t)=\sum_{n=0}^{\infty}U_n(x)t^n,\quad |t|<1\]

where

\[(1-2xt+t^2)G(x,t)=U_0(x)+U_1(x)t-2xtU_0(x)=1+2xt-2xt=1.\]

Hence we have

\[\sum_{n=0}^{\infty}U_n(x)t^n=G(x,t)=\frac{1}{1-2xt+t^2},\quad |t|<1.\]

This can be used, for instance, to prove that

\[\sum_{k=0}^nT_k(x)x^{n-k}=U_n(x),\quad n=0,1,2,\ldots.\]

In fact, we have for \(|t| < 1\)

\begin{align*} \sum_{n=0}^{\infty}\left(\sum_{k=0}^nT_k(x)x^{n-k}\right)t^n&=\sum_{k=0}^{\infty}\sum_{n=k}^{\infty}T_k(x)x^{n-k}t^n =\sum_{k=0}^{\infty}\sum_{n=0}^{\infty}T_k(x)x^nt^{n+k}=\sum_{k=0}^{\infty}T_k(x)t^k\cdot\sum_{n=0}^{\infty}(xt)^n\\[2.5mm] &=\frac{1-xt}{1-2xt+t^2}\cdot\frac{1}{1-xt}=\frac{1}{1-2xt+t^2}=\sum_{n=0}^{\infty}U_n(x)t^n. \end{align*}

In a similar way we can prove that

\[\sum_{k=0}^nP_k(x)P_{n-k}(x)=U_n(x),\quad n=0,1,2,\ldots,\]

where \(P_n(x)\) denotes the Legendre polynomial. In fact, we have for \(|t| < 1\)

\begin{align*} \sum_{n=0}^{\infty}\left(\sum_{k=0}^nP_k(x)P_{n-k}(x)\right)t^n&=\sum_{k=0}^{\infty}\sum_{n=k}^{\infty}P_k(x)P_{n-k}(x)t^n =\sum_{k=0}^{\infty}\sum_{n=0}^{\infty}P_k(x)P_n(x)t^{n+k}=\sum_{k=0}^{\infty}P_k(x)t^k\cdot\sum_{n=0}^{\infty}P_n(x)t^n\\[2.5mm] &=\frac{1}{\sqrt{1-2xt+t^2}}\cdot\frac{1}{\sqrt{1-2xt+t^2}}=\frac{1}{1-2xt+t^2}=\sum_{n=0}^{\infty}U_n(x)t^n. \end{align*}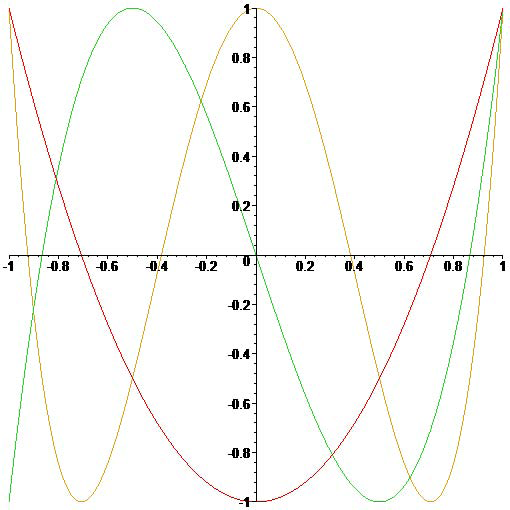

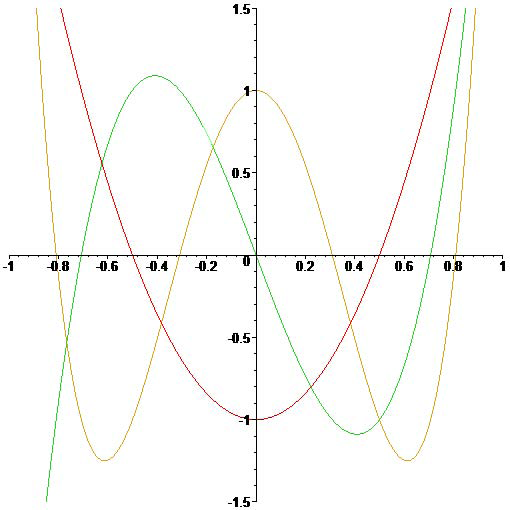The Chebyshev polynomials \(T_2(x)\), \(T_3(x)\) and \(T_4(x)\).	The Chebyshev polynomials \(U_2(x)\), \(U_3(x)\) and \(U_4(x)\).

---

Last modified on May 22, 2021