Special Functions – Orthogonal polynomials – Legendre polynomials
The Legendre polynomials are orthogonal on the interval \((-1,1)\) with respect to the weight function \(w(x)=1\). They can be defined by means of their Rodrigues formula:
\[P_n(x)=\frac{(-1)^n}{2^n\,n!}\,\frac{1}{w(x)}\,D^n\left[w(x)\,(1-x^2)^n\right] =\frac{(-1)^n}{2^n\,n!}\,D^n\left[(1-x^2)^n\right],\quad n=0,1,2,\ldots.\tag1\]This is a special case \(\alpha=\beta=0\) of the Jacobi polynomials:
\[P_n(x)=P_n^{(0,0)}(x)={}_2F_1\left(\genfrac{}{}{0pt}{}{-n,n+1}{1}\,;\,\frac{1-x}{2}\right),\quad n=0,1,2,\ldots.\tag2\]Further we have
\[P_n(-x)=(-1)^nP_n(x),\quad P_n(1)=1\quad\text{and}\quad P_n(-1)=(-1)^n,\quad n=0,1,2,\ldots.\]The leading coefficient of the polynomial \(P_n(x)\) equals
\[k_n=\frac{(-n)_n\,(n+1)_n}{(1)_n\,n!}\,\frac{(-1)^n}{2^n}=\frac{(2n)!}{2^n\,(n!)^2},\quad n=0,1,2,\ldots.\]The orthogonality relation is
\[\int_{-1}^1P_m(x)P_n(x)\,dx=\frac{2}{2n+1}\,\delta_{mn},\quad m,n\in\{0,1,2,\ldots\}.\tag3\]This can be shown by using the Rodrigues formula (1) and integration by parts
\[\int_{-1}^1P_m(x)P_n(x)\,dx=\frac{(-1)^n}{2^n\,n!}\,\int_{-1}^1P_m(x)D^n\left[(1-x^2)^n\right]\,dx =\frac{1}{2^n\,n!}\,\int_{-1}^1D^nP_m(x)\,(1-x^2)^n\,dx,\]which vanishes for \(m < n\). For \(m=n\) we have
\[\int_{-1}^1D^nP_n(x)\,(1-x^2)^n\,dx=k_n\,n!\,\int_{-1}^1(1-x^2)^n\,dx=\frac{(2n)!}{2^n\,n!}\,\int_{-1}^1(1-x^2)^n\,dx.\]Finally we have by using the substitution \(1-x=2t\)
\begin{align*} \int_{-1}^1(1-x^2)^n\,dx&=\int_{-1}^1(1-x)^n(1+x)^n\,dx=\int_0^1(2t)^n(2-2t)^n\,2\,dx=2^{2n+1}\,B(n+1,n+1)\\[2.5mm] &=2^{2n+1}\,\frac{\Gamma(n+1)\,\Gamma(n+1)}{\Gamma(2n+2)}=\frac{2^{2n+1}\,(n!)^2}{(2n+1)!},\quad n=0,1,2,\ldots. \end{align*}Hence we have
\[\int_{-1}^1\left\{P_n(x)\right\}^2\,dx=\frac{(2n)!}{2^{2n}\,(n!)^2}\,\frac{2^{2n+1}\,(n!)^2}{(2n+1)!}=\frac{2}{2n+1},\quad n=0,1,2,\ldots.\]This proves the orthogonality relation (3).
In order to find a generating function for the Legendre polynomials we use the hypergeometric representation (2) to find
\begin{align*} \sum_{n=0}^{\infty}P_n(x)t^n&=\sum_{n=0}^{\infty}\sum_{k=0}^n\frac{(-n)_k\,(n+1)_k}{(1)_k\,k!}\left(\frac{1-x}{2}\right)^kt^n =\sum_{k=0}^{\infty}\sum_{n=k}^{\infty}\frac{(-n)_k\,(n+1)_k}{k!\,k!}\left(\frac{1-x}{2}\right)^kt^n\\[2.5mm] &=\sum_{k=0}^{\infty}\sum_{n=0}^{\infty}\frac{(-n-k)_k\,(n+k+1)_k}{k!\,k!}\left(\frac{1-x}{2}\right)^kt^{n+k} =\sum_{k=0}^{\infty}\frac{(2k)!}{k!\,k!}\left(\frac{x-1}{2}\right)^kt^k\sum_{n=0}^{\infty}\frac{(2k+1)_n}{n!}\,t^n\\[2.5mm] &=\sum_{k=0}^{\infty}\frac{(2k)!}{k!\,k!}\left(\frac{x-1}{2}\right)^kt^k(1-t)^{-2k-1} =\sum_{k=0}^{\infty}\frac{(1/2)_k}{k!}\,\left[2(x-1)t\right]^k\,(1-t)^{-2k-1}\\[2.5mm] &=(1-t)^{-1}\left[1-\frac{2(x-1)t}{(1-t)^2}\right]^{-1/2}=\left[(1-t)^2-2(x-1)t\right]^{-1/2}=(1-2xt+t^2)^{-1/2} =\frac{1}{\sqrt{1-2xt+t^2}}. \end{align*}This proves the generating function
\[\frac{1}{\sqrt{1-2xt+t^2}}=\sum_{n=0}^{\infty}P_n(x)t^n.\tag4\]If we define \(F(x,t)=(1-2xt+t^2)^{-1/2}\), then we have
\[\frac{\partial}{\partial t}F(x,t)=-\frac{1}{2}(1-2xt+t^2)^{-3/2}\,(-2x+2t)=\frac{x-t}{(1-2xt+t^2)^{3/2}}.\]This implies that
\[(1-2xt+t^2)\frac{\partial}{\partial t}F(x,t)=(x-t)F(x,t).\]Now we use (4) to obtain
\[(1-2xt+t^2)\sum_{n=1}^{\infty}nP_n(x)t^{n-1}=(x-t)\sum_{n=0}^{\infty}P_n(x)t^n.\]This can also be written as
\[\sum_{n=1}^{\infty}nP_n(x)t^{n-1}-2x\sum_{n=1}^{\infty}nP_n(x)t^n+\sum_{n=1}^{\infty}nP_n(x)t^{n+1} =x\sum_{n=0}^{\infty}P_n(x)t^n-\sum_{n=0}^{\infty}P_n(x)t^{n+1}\]or equivalently
\[\sum_{n=0}^{\infty}(n+1)P_{n+1}(x)t^n-x\sum_{n=0}^{\infty}(2n+1)P_n(x)t^n+\sum_{n=0}^{\infty}(n+1)P_n(x)t^{n+1}=0.\]This leads to \(P_1(x)=xP_0(x)\) and the three-term recurrence relation
\[(n+1)P_{n+1}(x)-(2n+1)xP_n(x)+nP_{n-1}(x)=0,\quad n=1,2,3,\ldots.\]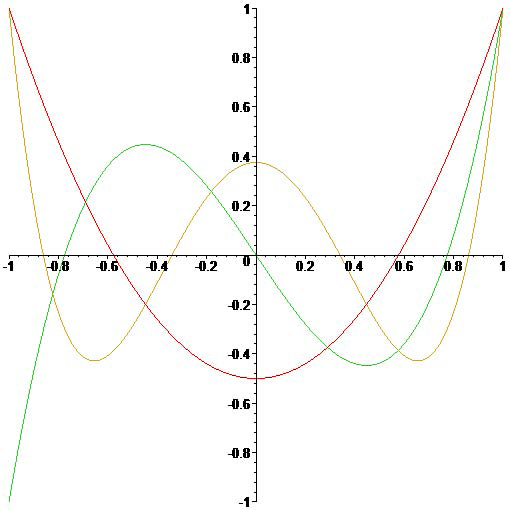
The Legendre polynomilas \(P_2(x)\), \(P_3(x)\) and \(P_4(x)\).
Last modified on May 22, 2021
 Teaching
Teaching

