Speciale Functies – De gamma- en de betafunctie – Eigenschappen van de gammafunctie

De gammafunctie \(\Gamma(z)\) wordt gedefinieerd door:

Definitie: \(\Gamma(z)=\displaystyle\int_0^{\infty}e^{-t}t^{z-1}\,dt,\quad\text{Re}(z)>0.\)

We hebben gezien dat \(\Gamma(z+1)=z\Gamma(z)\) voor \(\text{Re}(z)>0\), \(\Gamma(1)=1\) en dus \(\Gamma(n+1)=n!\) voor \(n=0,1,2,\ldots\) en \(\Gamma(\frac{1}{2})=\sqrt{\pi}\). Dus:

\[\Gamma(n+\tfrac{1}{2})=(n-\tfrac{1}{2})(n-\tfrac{3}{2})\cdots\tfrac{1}{2}\Gamma(\tfrac{1}{2}) =\frac{1\cdot3\cdot5\cdots(2n-1)}{2^n}\sqrt{\pi}=\frac{(2n)!}{2^{2n}n!}\sqrt{\pi},\quad n=1,2,3,\ldots.\]

Het bewijs van \(\Gamma(\frac{1}{2})=\sqrt{\pi}\) gebruikt de betafunctie \(B(u,v)\) gedefinieerd door

Definitie: \(B(u,v)=\displaystyle\int_0^1t^{u-1}(1-t)^{v-1}\,dt,\quad\text{Re}(u)>0,\quad\text{Re}(v)>0\).

In feite: omdat \(B(u,v)=\displaystyle\frac{\Gamma(u)\Gamma(v)}{\Gamma(u+v)}\) en \(B(u,v)=2\displaystyle\int_0^{\frac{1}{2}\pi}(\cos\varphi)^{2u-1}(\sin\varphi)^{2v-1}\,d\varphi\) voor \(\text{Re}(u)>0\) en \(\text{Re}(v)>0\) geldt

\[\{\Gamma(\tfrac{1}{2})\}^2=\displaystyle\frac{\Gamma(\frac{1}{2})\Gamma(\frac{1}{2})}{\Gamma(1)}=B(\tfrac{1}{2},\tfrac{1}{2}) =2\int_0^{\frac{1}{2}\pi}=2\cdot\frac{1}{2}\pi=\pi.\]

Nu volgt ook:

\[\int_0^{\frac{1}{2}\pi}(\sin\varphi)^{2n}\,d\varphi=\frac{1}{2}\cdot B(\tfrac{1}{2},n+\tfrac{1}{2})=\frac{1}{2}\cdot\frac{\Gamma(\frac{1}{2})\Gamma(n+\frac{1}{2})}{\Gamma(n+1)} =\frac{(2n)!}{2^{2n}(n!)^2}\cdot\frac{\pi}{2},\quad n=0,1,2,\ldots\]

en

\begin{align*} \int_0^{\frac{1}{2}\pi}(\sin\varphi)^{2n+1}\,d\varphi&=\frac{1}{2}\cdot B(\tfrac{1}{2},n+1)=\frac{1}{2}\cdot\frac{\Gamma(\frac{1}{2})\Gamma(n+1)}{\Gamma(n+\frac{3}{2})} =\frac{1}{2}\cdot\frac{\sqrt{\pi}\,n!}{(n+\frac{1}{2})\Gamma(n+\frac{1}{2})}\\[2.5mm] &=\frac{\sqrt{\pi}\,n!}{2n+1}\cdot\frac{2^{2n}n!}{(2n)!\sqrt{\pi}}=\frac{2^{2n}(n!)^2}{(2n+1)!},\quad n=0,1,2,\ldots. \end{align*}

Een ander belangrijk gevolg van deze relaties is verdubbelingsformule van Legendre:

Stelling: \(\Gamma(z)\Gamma(z+1/2)=2^{1-2z}\sqrt{\pi}\;\Gamma(2z),\quad\text{Re}(z)>0\).

Bewijs: Met behulp van de transformatie \(2\varphi=\tau\) volgt:

\begin{align*} \frac{\Gamma(z)\Gamma(z)}{\Gamma(2z)}&=B(z,z)=2\int_0^{\frac{1}{2}\pi}(\cos\varphi)^{2z-1}(\sin\varphi)^{2z-1}\,d\varphi=2\cdot2^{1-2z}\int_0^{\frac{1}{2}\pi}(\sin 2\varphi)^{2z-1}\,d\varphi\\[2.5mm] &=2^{1-2z}\int_0^\pi(\sin\tau)^{2z-1}\,d\tau=2^{1-2z}\cdot2\int_0^{\frac{1}{2}\pi}(\sin\tau)^{2z-1}\,d\tau=2^{1-2z}\cdot B(z,1/2) =2^{1-2z}\cdot\frac{\Gamma(z)\Gamma(1/2)}{\Gamma(z+1/2)},\quad\text{Re}(z)>0. \end{align*}

Nu gebruiken we \(\Gamma(\frac{1}{2})=\sqrt{\pi}\) om te concluderen dat \(\Gamma(z)\Gamma(z+1/2)=2^{1-2z}\sqrt{\pi}\;\Gamma(2z)\) voor \(\text{Re}(z)>0\).

De verdubbelingsformule van Legendre kan worden gegeneraliseerd tot de productformule van Gauss:

Stelling: \(\displaystyle\Gamma(z)\prod_{k=1}^{n-1}\Gamma(z+k/n)=n^{1/2-nz}(2\pi)^{(n-1)/2}\Gamma(nz)\) voor \(n\in\{1,2,3,\ldots\}\).

Het geval \(n=1\) is triviaal en het geval \(n=2\) is de verdubbelingsformule van Legendre.

Een andere eigenschap van de gammafunctie wordt gegeven door de reflectieformule van Euler:

Stelling: \(\Gamma(z)\Gamma(1-z)=\displaystyle\frac{\pi}{\sin\pi z},\quad z\neq0,\pm 1,\pm 2,\ldots\).

Bewijs: We gebruiken contourintegratie in het complexe vlak als volgt. We beperken ons eerst tot reële waarden van \(z\), zeg \(z=x\) met \(0 < x < 1\). Dan volgt:

\[\Gamma(x)\Gamma(1-x)=B(x,1-x)=\int_0^{\infty}\frac{t^{x-1}}{t+1}\,dt.\]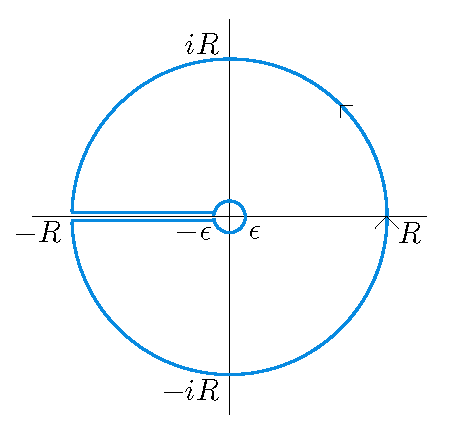

Om deze integraal te berekenen beschouwen we de contourintegraal

\[\int_{{\cal C}}\frac{z^{x-1}}{1-z}\,dz,\]

waarbij de contour \({\cal C}\) bestaat uit twee cirkels rond de oorsprong met straal \(R\) en \(\epsilon\) respectivelijk, die verbonden worden via de negatieve reële as van \(-R\) naar \(-\epsilon\). We volgen de buitenste cirkel met straal \(R\) in de positieve richting (tegen de wijzers van de klok in) en de binnenste cirkel met straal \(\epsilon\) in de negatieve richting (met de wijzers van de klok mee). Uit de residustelling volgt

\[\int_{{\cal C}}\frac{z^{x-1}}{1-z}\,dz=-2\pi i,\]

waarbij \(z^{x-1}\) de hoofdwaarde heeft. Hieruit volgt dat

\[-2\pi i=\int_{{\cal C}_1}\frac{z^{x-1}}{1-z}\,dz+\int_{{\cal C}_2}\frac{z^{x-1}}{1-z}\,dz +\int_{{\cal C}_3}\frac{z^{x-1}}{1-z}\,dz+\int_{{\cal C}_4}\frac{z^{x-1}}{1-z}\,dz,\]

waarbij \({\cal C}_1\) de buitenste cirkel met straal \(R\) is, \({\cal C}_2\) het lijnstuk van \(-R\) naar \(-\epsilon\), \({\cal C}_3\) de binnenste cirkel met straal \(\epsilon\) en \({\cal C}_4\) het lijnstuk van \(-\epsilon\) naar \(-R\). Dan volgt met \(z=Re^{i\theta}\) voor de buitenste cirkel

\[\int_{{\cal C}_1}\frac{z^{x-1}}{1-z}\,dz=\int_{-\pi}^{\pi}\frac{R^{x-1}e^{i(x-1)\theta}}{1-Re^{i\theta}}\,d\left(Re^{i\theta}\right) =\int_{-\pi}^{\pi}\frac{iR^xe^{ix\theta}}{1-Re^{i\theta}}\,d\theta.\]

Op dezelfde manier vinden we met \(z=\epsilon e^{i\theta}\) voor de binnenste cirkel

\[\int_{{\cal C}_3}\frac{z^{x-1}}{1-z}\,dz=\int_{\pi}^{-\pi}\frac{i\epsilon^xe^{ix\theta}}{1-\epsilon e^{i\theta}}\,d\theta.\]

Voor het lijnstuk van \(-R\) naar \(-\epsilon\) volgt met \(z=-t=te^{\pi i}\)

\[\int_{{\cal C}_2}\frac{z^{x-1}}{1-z}\,dz=\int_R^{\epsilon}\frac{t^{x-1}e^{i(x-1)\pi}}{1+t}\,d\left(te^{\pi i}\right) =\int_R^{\epsilon}\frac{t^{x-1}e^{ix\pi}}{1+t}\,dt.\]

Evenzo volgt met \(z=-t=te^{-\pi i}\)

\[\int_{{\cal C}_4}\frac{z^{x-1}}{1-z}\,dz=\int_{\epsilon}^R\frac{t^{x-1}e^{-ix\pi}}{1+t}\,dt.\]

Omdat \(0 < x < 1\) geldt

\[\lim\limits_{R\rightarrow\infty}\int_{-\pi}^{\pi}\frac{iR^xe^{ix\theta}}{1-Re^{i\theta}}\,d\theta=0\quad\text{and}\quad \lim\limits_{\epsilon\downarrow 0}\int_{\pi}^{-\pi}\frac{i\epsilon^xe^{ix\theta}}{1-\epsilon e^{i\theta}}\,d\theta=0.\]

Dus volgt

\[-2\pi i=\int_{\infty}^0\frac{t^{x-1}e^{ix\pi}}{1+t}\,dt+\int_0^{\infty}\frac{t^{x-1}e^{-ix\pi}}{1+t}\,dt,\]

of

\[-2\pi i=\left(e^{-ix\pi}-e^{ix\pi}\right)\int_0^{\infty}\frac{t^{x-1}}{1+t}\,dt\quad\Longrightarrow\quad \int_0^{\infty}\frac{t^{x-1}}{1+t}\,dt=\frac{2\pi i}{e^{ix\pi}-e^{-ix\pi}}=\frac{\pi}{\sin\pi x}.\]

Dit bewijst de stelling voor reële waarden van \(z\), zeg \(z=x\) met \(0 < x < 1\). Het volledige resultaat volgt door analytische voortzetting. Het kan eventueel ook als volgt. Als de formule geldt voor reële waarden van \(z\) met \(0 < z < 1\), dan geldt deze voor alle complexe \(z\) met \(0 < \text{Re}(z) < 1\) vanwege analyticiteit. Dan geldt het ook voor \(\text{Re}(z)=0\) met \(z\neq0\) vanwege continuïteit. Uiteindelijk volgt dan het volledige resultaat door verschuiving van \(z\) met behulp van de functionele relatie \(\Gamma(z+1)=z\Gamma(z)\) and \(\sin(z+\pi)=-\sin z\).

Merk op dat de reflectieformule van Euler geldt voor alle complexe waarden van \(z\) met \(z\neq0,-1,-2,\ldots\). We kunnen het ook schrijven als

\[\frac{1}{\Gamma(z)\Gamma(1-z)}=\frac{\sin\pi z}{\pi},\]

dat geldt voor alle \(z\in\mathbb{C}\). Een aardige toepassing is:

\begin{align*} \int_0^{\frac{1}{2}\pi}(\tan\varphi)^z\,d\varphi&=\frac{1}{2}\cdot B(-\tfrac{1}{2}z+\tfrac{1}{2},\tfrac{1}{2}z+\tfrac{1}{2}) =\frac{1}{2}\cdot\frac{\Gamma(-\frac{1}{2}z+\frac{1}{2},\frac{1}{2}z+\frac{1}{2})}{\Gamma(1)}\\[2.5mm] &=\frac{1}{2}\cdot\frac{\pi}{\sin(\frac{1}{2}(z+1)\pi)}=\frac{\pi/2}{\cos(\pi z/2)},\quad|\text{Re}(z)|<1. \end{align*}

Definitie: Twee functies \(f\) en \(g\) van een reële variabele \(x\) heten asymptotisch gelijk (notatie: \(f\sim g,\quad x\rightarrow\infty\)) als \(\lim\limits_{x\rightarrow\infty}\displaystyle\frac{f(x)}{g(x)}=1\).

Nu geldt de asymptotische formule van Stirling (met \(x\) een reële variabele):

Stelling: \(\Gamma(x+1)\sim x^{x+1/2}e^{-x}\sqrt{2\pi},\quad x\rightarrow\infty\).

Bewijs: Beschouw \(\displaystyle\Gamma(x+1)=\int_0^{\infty}e^{-t}t^x\,dt,\) waarbij \(x\in\mathbb{R}\). Dan gebruiken we de transformatie \(t=x(1+u)\)

\[\Gamma(x+1)=\int_{-1}^{\infty}e^{-x(1+u)}x^x(1+u)^xx\,du=x^{x+1}e^{-x}\int_{-1}^{\infty}e^{-xu}(1+u)^x\,du =x^{x+1}e^{-x}\int_{-1}^{\infty}e^{x(-u+\ln(1+u))}\,du.\]

De functie \(f(u)=-u+\ln(1+u)\) is gelijk aan nul voor \(u=0\). Voor andere waarden van \(u\) geldt \(f(u) < 0\). Hieruit volgt dat de integrand van de laatste integraal gelijk is aan \(1\) voor \(u=0\) en dat deze integrand heel erg klein wordt voor grote waarden van \(x\) voor andere waarden van \(u\). Voor grote waarden van \(x\) is dus alleen de integrand in de buurt van \(u=0\) van belang. Merk op dat

\[f(u)=-u+\ln(1+u)=-\frac{1}{2}u^2+{\cal O}(u^3)\quad u\rightarrow 0.\]

Hieruit volgt dat

\[\int_{-1}^{\infty}e^{x(-u+\ln(1+u))}\,du\sim\int_{-\infty}^{\infty}e^{-xu^2/2}\,du\quad x\rightarrow\infty.\]

Stel nu \(u=t\sqrt{2/x}\), dan volgt

\[\int_{-\infty}^{\infty}e^{-xu^2/2}\,du=x^{-1/2}\sqrt{2}\int_{-\infty}^{\infty}e^{-t^2}\,dt=x^{-1/2}\sqrt{2\pi}.\]

Dus volgt

\[\Gamma(x+1)\sim x^{x+1/2}e^{-x}\sqrt{2\pi},\quad x\rightarrow\infty,\]

waarmee de stelling bewezen is.

Merk op dat uit de asymptotische formule van Stirling volgt dat

\[n!\sim n^ne^{-n}\sqrt{2\pi n}\quad n\rightarrow\infty\]

en dat

\[\frac{\Gamma(n+a)}{\Gamma(n+b)}\sim n^{a-b}\quad n\rightarrow\infty.\]

De stelling kan worden uitgebreid voor \(z\) in het complexe vlak:

Stelling: Voor \(\delta>0\) geldt \(\Gamma(z+1)\sim z^{z+1/2}e^{-z}\sqrt{2\pi}\) voor \(|z|\rightarrow\infty\) met \(|\arg(z)|\leq\pi-\delta\).

De asymptotische formule van Stirling kan worden gebruikt voor een alternatief bewijs van de reflectieformule van Euler. Beschouw de functie

\[f(z)=\Gamma(z)\Gamma(1-z)\sin\pi z.\]

Dan volgt

\[f(z+1)=\Gamma(z+1)\Gamma(-z)\sin\pi(z+1)=z\Gamma(z)\cdot\frac{\Gamma(1-z)}{-z}\cdot{}-\sin\pi z=f(z).\]

Dus, \(f\) is periodiek met periode \(1\). Verder geldt

\[\lim\limits_{z\rightarrow 0}f(z)=\lim\limits_{z\rightarrow 0}\Gamma(z)\Gamma(1-z)\sin\pi z =\lim\limits_{z\rightarrow 0}\Gamma(z+1)\Gamma(1-z)\frac{\sin\pi z}{z}=\pi,\]

waaruit volgt dat \(f\) geen polen heeft. Dus, \(f\) is analytisch en periodiek met periode \(1\). Nu willen de stelling van Liouville toepassen, die gaat over gehele functies, oftewel functies die analytisch zijn op het gehele complexe vlak:

Stelling: Elke begrensde gehele functie is constant.

We willen dus aantonen dat \(f\) begrensd is. Omdat \(f\) periodiek is met periode \(1\) beschouwen we \(0\leq\text{Re}(z)\leq1\), zeg \(z=x+iy\) met \(x\) en \(y\) reëel en \(0\leq x\leq1\). Dus gledt

\[\sin\pi z=\frac{e^{i\pi z}-e^{-i\pi z}}{2i}\sim -\frac{1}{2i}e^{-i\pi z}=\frac{i}{2}e^{-i\pi z}\quad\text{for}\quad y\rightarrow\infty.\]

Nu passen we de asymptotische formule van Stirling toe

\[f(z)=\Gamma(z)\Gamma(1-z)\sin\pi z\sim z^{z-1/2}e^{-z}\sqrt{2\pi}\,(-z)^{-z+1/2}e^z\sqrt{2\pi}\,\frac{i}{2}e^{-i\pi z}.\]

Voor \(y>0\) geldt \(-z/z=e^{-\pi i}\). Dus, \(f(z)\sim\pi\) voor \(y\rightarrow\infty\). Hieruit volgt dat \(f\) begrensd is. Dus, uit de stelling van Liouvillevolgt dat \(f\) constant is. Met \(\displaystyle\lim\limits_{z\rightarrow 0}f(z)=\pi\) concluderen we dat \(f(z)=\pi\), waarmee de reflectieformule van Euler bewezen is.

De asymptotische formule van Stirling kan ook worden gebruikt voor een alternatief bewijs van de verdubbelingsformule van Legendre. Beschouw de functie

\[g(z)=2^{2z-1}\frac{\Gamma(z)\Gamma(z+1/2)}{\Gamma(1/2)\Gamma(2z)}.\]

Dan volgt

\[g(z+1)=2^{2z+1}\frac{\Gamma(z+1)\Gamma(z+3/2)}{\Gamma(1/2)\Gamma(2z+2)} =2^{2z+1}\frac{z\Gamma(z)(z+1/2)\Gamma(z+1/2)}{\Gamma(1/2)(2z+1)2z\Gamma(2z)}=g(z).\]

Verder geldt met \(\Gamma(\frac{1}{2})=\sqrt{\pi}\) en de asymptotische formule van Stirling dat

\[g(z)\sim 2^{2z-1}\frac{z^{z-1/2}e^{-z}\sqrt{2\pi}\,z^ze^{-z}\sqrt{2\pi}}{\sqrt{\pi}\,2^{2z-1/2}z^{2z-1/2}e^{-2z}\sqrt{2\pi}}=1.\]

Hieruit volgt dat

\[\lim\limits_{n\rightarrow\infty}g(z+n)=1,\]

ook voor gehele waarden van \(n\). Er geldt echter ook dat \(g(z+n)=g(z)\) voor gehele waarden van \(n\). Hieruit volgt dat \(g(z)=1\) voor alle \(z\), waarmee de verdubbelingsformule van Legendre bewezen is.

---

Last modified on 15 mei 2021