Special Functions – The gamma and the beta function – Properties of the gamma function

The gamma function \(\Gamma(z)\) is defined by:

Definition: \(\Gamma(z)=\displaystyle\int_0^{\infty}e^{-t}t^{z-1}\,dt,\quad\text{Re}(z)>0.\)

We have seen that \(\Gamma(z+1)=z\Gamma(z)\) for \(\text{Re}(z)>0\), \(\Gamma(1)=1\) and therefore \(\Gamma(n+1)=n!\) for \(n=0,1,2,\ldots\) and \(\Gamma(\frac{1}{2})=\sqrt{\pi}\). Hence:

\[\Gamma(n+\tfrac{1}{2})=(n-\tfrac{1}{2})(n-\tfrac{3}{2})\cdots\tfrac{1}{2}\Gamma(\tfrac{1}{2}) =\frac{1\cdot3\cdot5\cdots(2n-1)}{2^n}\sqrt{\pi}=\frac{(2n)!}{2^{2n}n!}\sqrt{\pi},\quad n=1,2,3,\ldots.\]

The proof of \(\Gamma(\frac{1}{2})=\sqrt{\pi}\) uses the beta function \(B(u,v)\) defined by

Definition: \(B(u,v)=\displaystyle\int_0^1t^{u-1}(1-t)^{v-1}\,dt,\quad\text{Re}(u)>0,\quad\text{Re}(v)>0\).

In fact: since \(B(u,v)=\displaystyle\frac{\Gamma(u)\Gamma(v)}{\Gamma(u+v)}\) and \(B(u,v)=2\displaystyle\int_0^{\frac{1}{2}\pi}(\cos\varphi)^{2u-1}(\sin\varphi)^{2v-1}\,d\varphi\) for \(\text{Re}(u)>0\) and \(\text{Re}(v)>0\) we have

\[\{\Gamma(\tfrac{1}{2})\}^2=\displaystyle\frac{\Gamma(\frac{1}{2})\Gamma(\frac{1}{2})}{\Gamma(1)}=B(\tfrac{1}{2},\tfrac{1}{2}) =2\int_0^{\frac{1}{2}\pi}=2\cdot\frac{1}{2}\pi=\pi.\]

Now we also have:

\[\int_0^{\frac{1}{2}\pi}(\sin\varphi)^{2n}\,d\varphi=\frac{1}{2}\cdot B(\tfrac{1}{2},n+\tfrac{1}{2})=\frac{1}{2}\cdot\frac{\Gamma(\frac{1}{2})\Gamma(n+\frac{1}{2})}{\Gamma(n+1)} =\frac{(2n)!}{2^{2n}(n!)^2}\cdot\frac{\pi}{2},\quad n=0,1,2,\ldots\]

and

\begin{align*} \int_0^{\frac{1}{2}\pi}(\sin\varphi)^{2n+1}\,d\varphi&=\frac{1}{2}\cdot B(\tfrac{1}{2},n+1)=\frac{1}{2}\cdot\frac{\Gamma(\frac{1}{2})\Gamma(n+1)}{\Gamma(n+\frac{3}{2})} =\frac{1}{2}\cdot\frac{\sqrt{\pi}\,n!}{(n+\frac{1}{2})\Gamma(n+\frac{1}{2})}\\[2.5mm] &=\frac{\sqrt{\pi}\,n!}{2n+1}\cdot\frac{2^{2n}n!}{(2n)!\sqrt{\pi}}=\frac{2^{2n}(n!)^2}{(2n+1)!},\quad n=0,1,2,\ldots. \end{align*}

Another important consequence of these relations is Legendre's duplication formula:

Theorem: \(\Gamma(z)\Gamma(z+1/2)=2^{1-2z}\sqrt{\pi}\;\Gamma(2z),\quad\text{Re}(z)>0\).

Proof: Using the transformation \(2\varphi=\tau\) we obtain:

\begin{align*} \frac{\Gamma(z)\Gamma(z)}{\Gamma(2z)}&=B(z,z)=2\int_0^{\frac{1}{2}\pi}(\cos\varphi)^{2z-1}(\sin\varphi)^{2z-1}\,d\varphi=2\cdot2^{1-2z}\int_0^{\frac{1}{2}\pi}(\sin 2\varphi)^{2z-1}\,d\varphi\\[2.5mm] &=2^{1-2z}\int_0^\pi(\sin\tau)^{2z-1}\,d\tau=2^{1-2z}\cdot2\int_0^{\frac{1}{2}\pi}(\sin\tau)^{2z-1}\,d\tau=2^{1-2z}\cdot B(z,1/2) =2^{1-2z}\cdot\frac{\Gamma(z)\Gamma(1/2)}{\Gamma(z+1/2)},\quad\text{Re}(z)>0. \end{align*}

Now we use \(\Gamma(\frac{1}{2})=\sqrt{\pi}\) to conclude that \(\Gamma(z)\Gamma(z+1/2)=2^{1-2z}\sqrt{\pi}\;\Gamma(2z)\) for \(\text{Re}(z)>0\).

Legendre’s duplication formula can be generalized to Gauss’s multiplication formula:

Theorem: \(\displaystyle\Gamma(z)\prod_{k=1}^{n-1}\Gamma(z+k/n)=n^{1/2-nz}(2\pi)^{(n-1)/2}\Gamma(nz)\) for \(n\in\{1,2,3,\ldots\}\).

The case \(n=1\) is trivial and the case \(n=2\) is Legendre's duplication formula.

Another property of the gamma function is given by Euler’s reflection formula:

Theorem: \(\Gamma(z)\Gamma(1-z)=\displaystyle\frac{\pi}{\sin\pi z},\quad z\neq0,\pm 1,\pm 2,\ldots\).

Proof: We use contour integration in the complex plane as follows. First we restrict to real values of \(z\), say \(z=x\) with \(0 < x < 1\). Then we have:

\[\Gamma(x)\Gamma(1-x)=B(x,1-x)=\int_0^{\infty}\frac{t^{x-1}}{t+1}\,dt.\]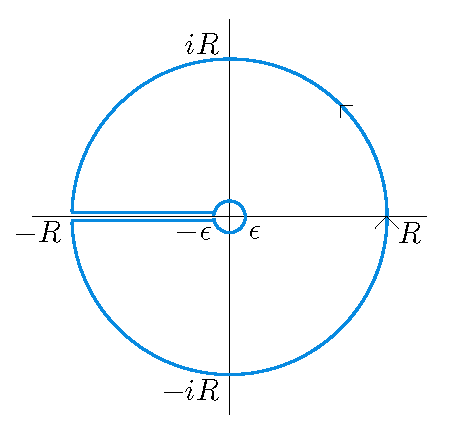

In order to evaluate this integral we consider the contour integral

\[\int_{{\cal C}}\frac{z^{x-1}}{1-z}\,dz,\]

where the contour \({\cal C}\) consists of two circles about the origin of radii \(R\) and \(\epsilon\) respectively, which are joined along the negative real axis from \(-R\) to \(-\epsilon\). Move along the outer circle with radius \(R\) in the positive (counterclockwise) direction and along the inner circle with radius \(\epsilon\) in the negative (clockwise) direction. By the residue theorem we have

\[\int_{{\cal C}}\frac{z^{x-1}}{1-z}\,dz=-2\pi i,\]

when \(z^{x-1}\) has its principal value. This implies that

\[-2\pi i=\int_{{\cal C}_1}\frac{z^{x-1}}{1-z}\,dz+\int_{{\cal C}_2}\frac{z^{x-1}}{1-z}\,dz +\int_{{\cal C}_3}\frac{z^{x-1}}{1-z}\,dz+\int_{{\cal C}_4}\frac{z^{x-1}}{1-z}\,dz,\]

where \({\cal C}_1\) denotes the outer circle with radius \(R\), \({\cal C}_2\) denotes the line segment from \(-R\) to \(-\epsilon\), \({\cal C}_3\) denotes the inner circle with radius \(\epsilon\) and \({\cal C}_4\) denotes the line segment from \(-\epsilon\) to \(-R\). Then we have by writing \(z=Re^{i\theta}\) for the outer circle

\[\int_{{\cal C}_1}\frac{z^{x-1}}{1-z}\,dz=\int_{-\pi}^{\pi}\frac{R^{x-1}e^{i(x-1)\theta}}{1-Re^{i\theta}}\,d\left(Re^{i\theta}\right) =\int_{-\pi}^{\pi}\frac{iR^xe^{ix\theta}}{1-Re^{i\theta}}\,d\theta.\]

In the same way we have by writing \(z=\epsilon e^{i\theta}\) for the inner circle

\[\int_{{\cal C}_3}\frac{z^{x-1}}{1-z}\,dz=\int_{\pi}^{-\pi}\frac{i\epsilon^xe^{ix\theta}}{1-\epsilon e^{i\theta}}\,d\theta.\]

For the line segment from \(-R\) to \(-\epsilon\) we have by writing \(z=-t=te^{\pi i}\)

\[\int_{{\cal C}_2}\frac{z^{x-1}}{1-z}\,dz=\int_R^{\epsilon}\frac{t^{x-1}e^{i(x-1)\pi}}{1+t}\,d\left(te^{\pi i}\right) =\int_R^{\epsilon}\frac{t^{x-1}e^{ix\pi}}{1+t}\,dt.\]

In the same way we have by writing \(z=-t=te^{-\pi i}\)

\[\int_{{\cal C}_4}\frac{z^{x-1}}{1-z}\,dz=\int_{\epsilon}^R\frac{t^{x-1}e^{-ix\pi}}{1+t}\,dt.\]

Since \(0 < x < 1\) we have

\[\lim\limits_{R\rightarrow\infty}\int_{-\pi}^{\pi}\frac{iR^xe^{ix\theta}}{1-Re^{i\theta}}\,d\theta=0\quad\text{and}\quad \lim\limits_{\epsilon\downarrow 0}\int_{\pi}^{-\pi}\frac{i\epsilon^xe^{ix\theta}}{1-\epsilon e^{i\theta}}\,d\theta=0.\]

Hence we have

\[-2\pi i=\int_{\infty}^0\frac{t^{x-1}e^{ix\pi}}{1+t}\,dt+\int_0^{\infty}\frac{t^{x-1}e^{-ix\pi}}{1+t}\,dt,\]

or

\[-2\pi i=\left(e^{-ix\pi}-e^{ix\pi}\right)\int_0^{\infty}\frac{t^{x-1}}{1+t}\,dt\quad\Longrightarrow\quad \int_0^{\infty}\frac{t^{x-1}}{1+t}\,dt=\frac{2\pi i}{e^{ix\pi}-e^{-ix\pi}}=\frac{\pi}{\sin\pi x}.\]

This proves the theorem for real values of \(z\), say \(z=x\) with \(0 < x < 1\). The full result follows by analytic continuation. Alternatively, the result can be obtained as follows. If the formula holds for real values of \(z\) with \(0 < z < 1\), then it holds for all complex \(z\) with \(0 < \text{Re}(z) < 1\) by analyticity. Then it also holds for \(\text{Re}(z)=0\) with \(z\neq0\) by continuity. Finally, the full result follows by shifting \(z\) using the functional relation \(\Gamma(z+1)=z\Gamma(z)\) and \(\sin(z+\pi)=-\sin z\).

Note that Euler's reflection formula holds for all complex values of \(z\) with \(z\neq0,-1,-2,\ldots\). Instead we may write

\[\frac{1}{\Gamma(z)\Gamma(1-z)}=\frac{\sin\pi z}{\pi},\]

which holds for all \(z\in\mathbb{C}\). A nice application is:

\begin{align*} \int_0^{\frac{1}{2}\pi}(\tan\varphi)^z\,d\varphi&=\frac{1}{2}\cdot B(-\tfrac{1}{2}z+\tfrac{1}{2},\tfrac{1}{2}z+\tfrac{1}{2}) =\frac{1}{2}\cdot\frac{\Gamma(-\frac{1}{2}z+\frac{1}{2},\frac{1}{2}z+\frac{1}{2})}{\Gamma(1)}\\[2.5mm] &=\frac{1}{2}\cdot\frac{\pi}{\sin(\frac{1}{2}(z+1)\pi)}=\frac{\pi/2}{\cos(\pi z/2)},\quad|\text{Re}(z)|<1. \end{align*}

Definition: Two functions \(f\) and \(g\) of a real variable \(x\) are called asymptotically equal (notation: \(f\sim g,\quad x\rightarrow\infty\)) if \(\lim\limits_{x\rightarrow\infty}\displaystyle\frac{f(x)}{g(x)}=1\).

Now we have Stirling's asymptotic formula (with \(x\) a real variable):

Theorem: \(\Gamma(x+1)\sim x^{x+1/2}e^{-x}\sqrt{2\pi},\quad x\rightarrow\infty\).

Proof: Consider \(\displaystyle\Gamma(x+1)=\int_0^{\infty}e^{-t}t^x\,dt,\) where \(x\in\mathbb{R}\). Then we obtain using the transformation \(t=x(1+u)\)

\[\Gamma(x+1)=\int_{-1}^{\infty}e^{-x(1+u)}x^x(1+u)^xx\,du=x^{x+1}e^{-x}\int_{-1}^{\infty}e^{-xu}(1+u)^x\,du =x^{x+1}e^{-x}\int_{-1}^{\infty}e^{x(-u+\ln(1+u))}\,du.\]

The function \(f(u)=-u+\ln(1+u)\) equals zero for \(u=0\). For other values of \(u\) we have \(f(u) < 0\). This implies that the integrand of the last integral equals \(1\) at \(u=0\) and that this integrand becomes very small for large values of \(x\) at other values of \(u\). So for large values of \(x\) we only have to deal with the integrand near \(u=0\). Note that we have

\[f(u)=-u+\ln(1+u)=-\frac{1}{2}u^2+{\cal O}(u^3)\quad u\rightarrow 0.\]

This implies that

\[\int_{-1}^{\infty}e^{x(-u+\ln(1+u))}\,du\sim\int_{-\infty}^{\infty}e^{-xu^2/2}\,du\quad x\rightarrow\infty.\]

If we set \(u=t\sqrt{2/x}\) we have

\[\int_{-\infty}^{\infty}e^{-xu^2/2}\,du=x^{-1/2}\sqrt{2}\int_{-\infty}^{\infty}e^{-t^2}\,dt=x^{-1/2}\sqrt{2\pi}.\]

Hence we have

\[\Gamma(x+1)\sim x^{x+1/2}e^{-x}\sqrt{2\pi},\quad x\rightarrow\infty,\]

which proves the theorem.

Note that Stirling's asymptotic formula implies that

\[n!\sim n^ne^{-n}\sqrt{2\pi n}\quad n\rightarrow\infty\]

and that

\[\frac{\Gamma(n+a)}{\Gamma(n+b)}\sim n^{a-b}\quad n\rightarrow\infty.\]

The theorem can be extended for \(z\) in the complex plane:

Theorem: For \(\delta>0\) we have \(\Gamma(z+1)\sim z^{z+1/2}e^{-z}\sqrt{2\pi}\) for \(|z|\rightarrow\infty\) with \(|\arg(z)|\leq\pi-\delta\).

Stirling's asymptotic formula can be used to give an alternative proof for Euler's reflection formula. Consider the function

\[f(z)=\Gamma(z)\Gamma(1-z)\sin\pi z.\]

Then we have

\[f(z+1)=\Gamma(z+1)\Gamma(-z)\sin\pi(z+1)=z\Gamma(z)\cdot\frac{\Gamma(1-z)}{-z}\cdot{}-\sin\pi z=f(z).\]

Hence, \(f\) is periodic with period \(1\). Further we have

\[\lim\limits_{z\rightarrow 0}f(z)=\lim\limits_{z\rightarrow 0}\Gamma(z)\Gamma(1-z)\sin\pi z =\lim\limits_{z\rightarrow 0}\Gamma(z+1)\Gamma(1-z)\frac{\sin\pi z}{z}=\pi,\]

which implies that \(f\) has no poles. Hence, \(f\) is analytic and periodic with period \(1\). Now we want to apply Liouville's theorem for entire functions, id est functions which are analytic on the whole complex plane:

Theorem: Every bounded entire function is constant.

Therefore, we want to show that \(f\) is bounded. Since \(f\) is periodic with period \(1\) we consider \(0\leq\text{Re}(z)\leq1\), say \(z=x+iy\) with \(x\) and \(y\) real and \(0\leq x\leq1\). Then we have

\[\sin\pi z=\frac{e^{i\pi z}-e^{-i\pi z}}{2i}\sim -\frac{1}{2i}e^{-i\pi z}=\frac{i}{2}e^{-i\pi z}\quad\text{for}\quad y\rightarrow\infty.\]

Now we apply Stirling's asymptotic formula to obtain

\[f(z)=\Gamma(z)\Gamma(1-z)\sin\pi z\sim z^{z-1/2}e^{-z}\sqrt{2\pi}\,(-z)^{-z+1/2}e^z\sqrt{2\pi}\,\frac{i}{2}e^{-i\pi z}.\]

For \(y>0\) we have \(-z/z=e^{-\pi i}\). Hence, \(f(z)\sim\pi\) for \(y\rightarrow\infty\). This implies that \(f\) is bounded. So, Liouville's theorem implies that \(f\) is constant. Using \(\displaystyle\lim\limits_{z\rightarrow 0}f(z)=\pi\) we conclude that \(f(z)=\pi\), which proves Euler's reflection formula.

Stirling's asymptotic formula can also be used to give an alternative proof for Legendre's duplication formula. Consider the function

\[g(z)=2^{2z-1}\frac{\Gamma(z)\Gamma(z+1/2)}{\Gamma(1/2)\Gamma(2z)}.\]

Then we have

\[g(z+1)=2^{2z+1}\frac{\Gamma(z+1)\Gamma(z+3/2)}{\Gamma(1/2)\Gamma(2z+2)} =2^{2z+1}\frac{z\Gamma(z)(z+1/2)\Gamma(z+1/2)}{\Gamma(1/2)(2z+1)2z\Gamma(2z)}=g(z).\]

Further we have using \(\Gamma(\frac{1}{2})=\sqrt{\pi}\) and Stirling's asymptotic formula that

\[g(z)\sim 2^{2z-1}\frac{z^{z-1/2}e^{-z}\sqrt{2\pi}\,z^ze^{-z}\sqrt{2\pi}}{\sqrt{\pi}\,2^{2z-1/2}z^{2z-1/2}e^{-2z}\sqrt{2\pi}}=1.\]

This implies that

\[\lim\limits_{n\rightarrow\infty}g(z+n)=1,\]

also for integer values of \(n\). On the other hand we have \(g(z+n)=g(z)\) for integer values of \(n\). This implies that \(g(z)=1\) for all \(z\), which proves Legendre's duplication formula.

---

Last modified on May 15, 2021