Special Functions – Bessel functions – Properties

The Bessel function \(J_{\nu}(z)\) of the first kind of order \(\nu\) is defined by

\[J_{\nu}(z)=\frac{(z/2)^{\nu}}{\Gamma(\nu+1)}\,{}_0F_1\left(\genfrac{}{}{0pt}{}{-}{\nu+1}\,;\,-\frac{z^2}{4}\right) =\left(\frac{z}{2}\right)^{\nu}\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(\nu+k+1)\,k!}\left(\frac{z}{2}\right)^{2k}\tag1\]

and the Bessel function \(Y_{\nu}(z)\) of the second kind of order \(\nu\) is given by

\[Y_{\nu}(z):=\frac{J_{\nu}(z)\cos\nu\pi-J_{-\nu}(z)}{\sin\nu\pi}\;\;\text{for}\;\;\nu\notin\{0,1,2,\ldots\} \quad\text{and}\quad Y_n(z):=\lim\limits_{\nu\rightarrow n}Y_{\nu}(z)\;\;\text{for}\;\;n\in\{0,1,2,\ldots\}.\tag2\]

Both are solutions of the Bessel differential equation

\[z^2y''(z)+zy'(z)+\left(z^2-\nu^2\right)y(z)=0,\quad\nu\geq0.\]

Application of Abel's theorem to this Bessel differential equation shows that the Wronskian \(W(z)\) of two solutions satisfies the differential equation \(W'(z)+\displaystyle\frac{1}{z}W(z)=0\), which implies that \(W(z)=\displaystyle\frac{c}{z}\) for some constant \(c\). In fact we have

Theorem: \(W(J_{\nu},J_{-\nu})(z)=-\displaystyle\frac{2\sin\nu\pi}{\pi z}\) and \(W(J_{\nu},Y_{\nu})(z)=\displaystyle\frac{2}{\pi z}\).

For \(\nu\geq0\) this implies that \(J_{\nu}(z)\) and \(J_{-\nu}(z)\) are linearly independent if \(\nu\notin\{0,1,2,\ldots\}\) and that \(J_{\nu}(z)\) and \(Y_{\nu}(z)\) are linearly independent for all \(\nu\geq0\).

Proof: Note that

\begin{align*} W(J_{\nu},Y_{\nu})(z)&=J_{\nu}(z)Y_{\nu}'(z)-J_{\nu}'(z)Y_{\nu}(z) =J_{\nu}(z)\frac{J_{\nu}'(z)\cos\nu\pi-J_{-\nu}'(z)}{\sin\nu\pi}-J_{\nu}'(z)\frac{J_{\nu}(z)\cos\nu\pi-J_{-\nu}(z)}{\sin\nu\pi}\\[2.5mm] &=-\frac{J_{\nu}(z)J_{-\nu}'(z)-J_{\nu}'(z)J_{-\nu}(z)}{\sin\nu\pi}=-\frac{W(J_{\nu},J_{-\nu})(z)}{\sin\nu\pi}. \end{align*}

Now we use the definition (1) to obtain

\[J_{\nu}(z)=\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(\nu+k+1)\,k!}\cdot\frac{z^{\nu+2k}}{2^{\nu+2k}} \quad\Longrightarrow\quad J_{\nu}'(z)=\sum_{k=0}^{\infty}\frac{(-1)^k(\nu+2k)}{\Gamma(\nu+k+1)\,k!}\cdot\frac{z^{\nu+2k-1}}{2^{\nu+2k}}\]

and

\[J_{-\nu}(z)=\sum_{m=0}^{\infty}\frac{(-1)^m}{\Gamma(-\nu+m+1)\,m!}\cdot\frac{z^{-\nu+2m}}{2^{-\nu+2m}} \quad\Longrightarrow\quad J_{-\nu}'(z)=\sum_{m=0}^{\infty}\frac{(-1)^m(-\nu+2m)}{\Gamma(-\nu+m+1)\,m!}\cdot\frac{z^{-\nu+2m-1}}{2^{-\nu+2m}}.\]

Hence we have

\begin{align*} z\,W(J_{\nu},J_{-\nu})(z)&=z\left[J_{\nu}(z)J_{-\nu}'(z)-J_{\nu}'(z)J_{-\nu}(z)\right]\\[2.5mm] &=\sum_{k=0}^{\infty}\sum_{m=0}^{\infty}\frac{(-1)^{k+m}(-\nu+2m)}{\Gamma(\nu+k+1)\Gamma(-\nu+m+1)\,k!\,m!} \cdot\frac{z^{2k+2m}}{2^{2k+2m}}-\sum_{k=0}^{\infty}\sum_{m=0}^{\infty} \frac{(-1)^{k+m}(\nu+2k)}{\Gamma(\nu+k+1)\Gamma(-\nu+m+1)\,k!\,m!}\cdot\frac{z^{2k+2m}}{2^{2k+2m}}\\[2.5mm] &=-\sum_{k=0}^{\infty}\sum_{m=0}^{\infty}\frac{(-1)^{k+m}(2\nu+2k-2m)}{\Gamma(\nu+k+1)\Gamma(-\nu+m+1)\,k!\,m!}\cdot\frac{z^{2k+2m}}{2^{2k+2m}}. \end{align*}

This implies that

\[\lim\limits_{z\rightarrow 0}z\,W(J_{\nu},J_{-\nu})(z)=-\frac{2\nu}{\Gamma(\nu+1)\Gamma(-\nu+1)} =-\frac{2\nu}{\nu\Gamma(\nu)\Gamma(1-\nu)}=-\frac{2\sin\nu\pi}{\pi}.\]

Using the definition (1) we obtain

\[\frac{d}{dz}\left[z^{\nu}J_{\nu}(z)\right] =\frac{d}{dz}\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(\nu+k+1)\,k!}\cdot\frac{z^{2\nu+2k}}{2^{\nu+2k}} =\sum_{k=0}^{\infty}\frac{(-1)^k(2\nu+2k)}{\Gamma(\nu+k+1)\,k!}\cdot\frac{z^{2\nu+2k-1}}{2^{\nu+2k}} =\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(\nu+k)\,k!}\cdot\frac{z^{2\nu+2k-1}}{2^{\nu+2k-1}}=z^{\nu}J_{\nu-1}(z).\]

Hence we have

\[\frac{d}{dz}\left[z^{\nu}J_{\nu}(z)\right]=z^{\nu}J_{\nu-1}(z)\quad\Longleftrightarrow\quad zJ_{\nu}'(z)+\nu J_{\nu}(z)=zJ_{\nu-1}(z).\tag3\]

Similarly we have

\[\frac{d}{dz}\left[z^{-\nu}J_{\nu}(z)\right] =\frac{d}{dz}\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(\nu+k+1)\,k!}\cdot\frac{z^{2k}}{2^{\nu+2k}} =\sum_{k=0}^{\infty}\frac{(-1)^k\,2k}{\Gamma(\nu+k+1)\,k!}\cdot\frac{z^{2k-1}}{2^{\nu+2k}} =\sum_{k=0}^{\infty}\frac{(-1)^{k+1}}{\Gamma(\nu+k+2)\,k!}\cdot\frac{z^{2k+1}}{2^{\nu+2k+1}}=-z^{-\nu}J_{\nu+1}(z).\]

Hence we have

\[\frac{d}{dz}\left[z^{-\nu}J_{\nu}(z)\right]=-z^{-\nu}J_{\nu+1}(z)\quad\Longleftrightarrow\quad zJ_{\nu}'(z)-\nu J_{\nu}(z)=-zJ_{\nu+1}(z).\tag4\]

Elimination of \(J_{\nu}'(z)\) from (3) and (4) gives

\[J_{\nu-1}(z)+J_{\nu+1}(z)=\frac{2\nu}{z}J_{\nu}(z)\]

and elimination of \(J_{\nu}(z)\) from (3) and (4) gives

\[J_{\nu-1}(z)-J_{\nu+1}(z)=2J_{\nu}'(z).\]

Special cases

For \(\nu=1/2\) we have from the definition (1) by using Legendre's duplication formula for the gamma function

\[J_{1/2}(x)=\sqrt{\frac{x}{2}}\;\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(k+3/2)\,k!}\left(\frac{x}{2}\right)^{2k} =\sqrt{\frac{2x}{\pi}}\;\sum_{k=0}^{\infty}\frac{(-1)^k}{(2k+1)!}\,x^{2k}=\sqrt{\frac{2}{\pi x}}\;\sin x,\quad x>0\]

and for \(\nu=-1/2\) we have

\[J_{-1/2}(x)=\sqrt{\frac{2}{x}}\;\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(k+1/2)\,k!}\left(\frac{x}{2}\right)^{2k} =\sqrt{\frac{2}{\pi x}}\;\sum_{k=0}^{\infty}\frac{(-1)^k}{(2k)!}\,x^{2k}=\sqrt{\frac{2}{\pi x}}\;\cos x,\quad x>0.\]

Note that the definition (2) implies that

\[Y_{1/2}(x)=-J_{-1/2}(x)=-\sqrt{\frac{2}{\pi x}}\;\cos x\quad\text{and}\quad Y_{-1/2}(x)=J_{1/2}(x)=\sqrt{\frac{2}{\pi x}}\;\sin x,\quad x>0.\]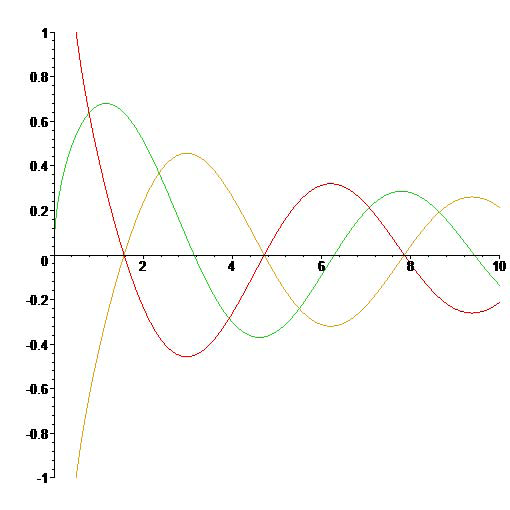

The Bessel functions \(J_{1/2}(x)\), \(J_{-1/2}(x)\) and \(Y_{1/2}(x)\).

Hankel functions

The functions \(H_{\nu}^{(1)}(z)\) and \(H_{\nu}^{(2)}(z)\) are defined by

\[H_{\nu}^{(1)}(z):=J_{\nu}(z)+iY_{\nu}(z)\quad\text{and}\quad H_{\nu}^{(2)}(z):=J_{\nu}(z)-iY_{\nu}(z).\]

These functions are called Hankel functions or Bessel functions of the third kind.

Note that these definitions imply that

\[J_{\nu}(z)=\frac{H_{\nu}^{(1)}(z)+H_{\nu}^{(2)}(z)}{2}\quad\text{and}\quad Y_{\nu}(z)=\frac{H_{\nu}^{(1)}(z)-H_{\nu}^{(2)}(z)}{2i}.\]

Further we have

\[H_{-1/2}^{(1)}(x)=J_{-1/2}(x)+iY_{-1/2}(x)=\sqrt{\frac{2}{\pi x}}\,(\cos x+i\sin x)=\sqrt{\frac{2}{\pi x}}\,e^{ix},\quad x>0\]

and

\[H_{-1/2}^{(2)}(x)=J_{-1/2}(x)-iY_{-1/2}(x)=\sqrt{\frac{2}{\pi x}}\,(\cos x-i\sin x)=\sqrt{\frac{2}{\pi x}}\,e^{-ix},\quad x>0.\]

Similarly we have

\[H_{1/2}^{(1)}(x)=J_{1/2}(x)+iY_{1/2}(x)=\sqrt{\frac{2}{\pi x}}\,(\sin x-i\cos x)=-i\sqrt{\frac{2}{\pi x}}\,e^{ix},\quad x>0\]

and

\[H_{1/2}^{(2)}(x)=J_{1/2}(x)-iY_{1/2}(x)=\sqrt{\frac{2}{\pi x}}\,(\sin x+i\cos x)=i\sqrt{\frac{2}{\pi x}}\,e^{-ix},\quad x>0.\]

Modified Bessel functions

The modified Bessel function \(I_{\nu}(z)\) of the first kind of order \(\nu\) is defined by

\[I_{\nu}(z):=\frac{(z/2)^{\nu}}{\Gamma(\nu+1)}\,{}_0F_1\left(\genfrac{}{}{0pt}{}{-}{\nu+1}\,;\,\frac{z^2}{4}\right) =\left(\frac{z}{2}\right)^{\nu}\sum_{k=0}^{\infty}\frac{1}{\Gamma(\nu+k+1)\,k!}\left(\frac{z}{2}\right)^{2k}.\]

For \(\nu\geq0\) this is a solution of the modified Bessel differential equation

\[z^2y''(z)+zy'(z)-\left(z^2+\nu^2\right)y(z)=0,\quad\nu\geq0.\]

For \(\nu\notin\{0,1,2,\ldots\}\) we have that \(I_{-\nu}(z)\) is a second solution of this differential equation and the two solutions \(I_{\nu}(z)\) and \(I_{-\nu}(z)\) are linearly independent. For \(\nu=n\in\{0,1,2,\ldots\}\) we have \(I_{-n}(z)=I_n(z)\).

The modified Bessel function \(K_{\nu}(z)\) of the second kind of order \(\nu\) is defined by

\[K_{\nu}(z):=\frac{\pi}{2\sin\nu\pi}\left[I_{-\nu}(z)-I_{\nu}(z)\right]\;\;\text{for}\;\;\nu\notin\{0,1,2,\ldots\} \quad\text{and}\quad K_n(z):=\lim\limits_{\nu\rightarrow n}K_{\nu}(z)\;\;\text{for}\;\;n\in\{0,1,2,\ldots\}.\]

Now we have for \(x>0\)

\[I_{1/2}(x)=\sqrt{\frac{2}{\pi x}}\,\sinh x,\quad I_{-1/2}(x)=\sqrt{\frac{2}{\pi x}}\,\cosh x \quad\text{and}\quad K_{1/2}(x)=K_{-1/2}(x)=\sqrt{\frac{\pi}{2x}}\,e^{-x}.\]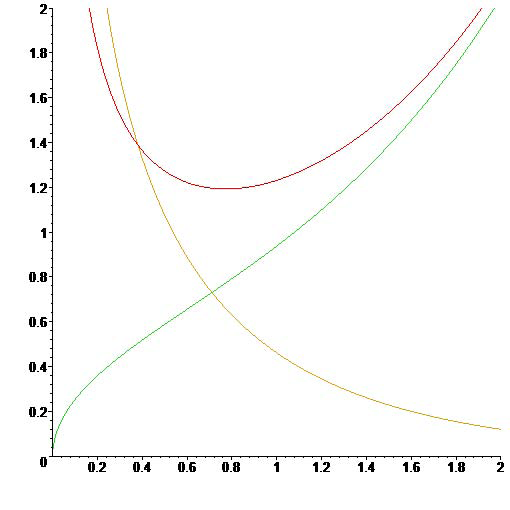

The modified Bessel functions \(I_{1/2}(x)\), \(I_{-1/2}(x)\) and \(K_{1/2}(x)\).

---

Last modified on September 29, 2021