Special Functions – Bessel functions – Zeros

The Bessel function \(J_{\nu}(z)\) of the first kind of order \(\nu\in\mathbb{R}\) can be written as

\[J_{\nu}(z)=\left(\frac{z}{2}\right)^{\nu}\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(\nu+k+1)\,k!}\left(\frac{z}{2}\right)^{2k}.\tag1\]

This is a solution of the Bessel differential equation which can be written as

\[z^2y''(z)+zy'(z)+(z^2-\nu^2)y(z)=0,\quad\nu\in\mathbb{R}.\tag2\]

We will derive some basic facts about the zeros of the Bessel function \(J_{\nu}(z)\) and its derivative \(J_{\nu}'(z)\). We have

Theorem: All zeros of \(J_{\nu}(z)\), except \(z=0\) possibly, are simple.

Proof: If \(z_0\neq0\) is a multiple zero of \(J_{\nu}(z)\), then we have at least that \(J_{\nu}(z_0)=0\) and \(J_{\nu}'(z_0)=0\). Since \(z_0\ne 0\) it follows from the differential equation (2) that also \(J_{\nu}''(z_0)=0\). Iteration then leads to \(J_{\nu}^{(n)}(z_0)=0\) for all \(n\in\{0,1,2,\ldots\}\), which implies that \(J_{\nu}(z)\) is identically zero. This is a trivial contradiction.

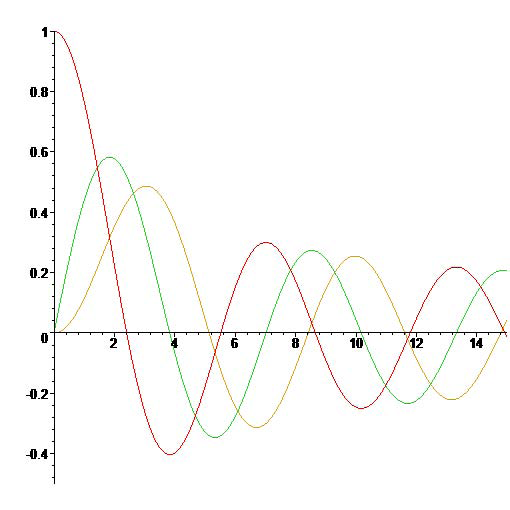
The Bessel functions \(J_0(x)\), \(J_1(x)\) and \(J_2(x)\).

Theorem: All zeros of \(J_{\nu}'(z)\), except \(z=0\) or \(z=\pm\nu\) possibly, are simple.

Proof: If \(z_0\) is a multiple zero of \(J_{\nu}'(z)\), then we have at least that \(J_{\nu}'(z_0)=0\) and \(J_{\nu}''(z_0)=0\). For \(z_0\neq0\) and \(z_0\neq\pm\nu\) it then follows from the differential equation (2) that also \(J_{\nu}(z_0)=0\). Again this leads to \(J_{\nu}(z)\) being identically zero which is clearly not true.

Theorem: If \(z_0\in\mathbb{C}\) is a zero of \(J_{\nu}(z)\), then also \(-z_0\) and \(\pm\overline{z_0}\).

Proof: Since this is trivial for \(z_0=0\) we now assume that \(z_0\neq0\). Then it follows from (1) that \(z_0\) is a zero of

\[\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(\nu+k+1)\,k!}\left(\frac{z}{2}\right)^{2k}.\]

This series is even and has real coefficients. This implies that \(-z_0\) and \(\pm\overline{z_0}\) are zeros too.

Theorem: If \(z_0\in\mathbb{C}\) is a zero of \(J_{\nu}'(z)\), then also \(-z_0\) and \(\pm\overline{z_0}\).

Proof: From (1) it follows that

\[J_{\nu}'(z)=\left(\frac{z}{2}\right)^{\nu-1}\sum_{k=0}^{\infty}\frac{(-1)^k\left(\frac{\nu}{2}+k\right)}{\Gamma(\nu+k+1)\,k!} \left(\frac{z}{2}\right)^{2k}.\]

Hence, if \(z_0\neq0\) is a zero of \(J_{\nu}'(z)\) it must be a zero of

\[\sum_{k=0}^{\infty}\frac{(-1)^k\left(\frac{\nu}{2}+k\right)}{\Gamma(\nu+k+1)\,k!}\left(\frac{z}{2}\right)^{2k},\]

which is even and also has real coefficients. This implies that \(-z_0\) and \(\pm\overline{z_0}\) are zeros too.

Lemma: For \(\nu>-1\) we have

\[(a^2-b^2)\int_0^ztJ_{\nu}(at)J_{\nu}(bt)\,dt=z\left[bJ_{\nu}(az)J_{\nu}'(bz)-aJ_{\nu}'(az)J_{\nu}(bz)\right].\tag3\]

Proof: The differential equation (2) implies that

\[c^2z^2J_{\nu}''(cz)+czJ_{\nu}'(cz)+\left(c^2z^2-\nu^2\right)J_{\nu}(cz)=0,\quad c\in\mathbb{C}.\]

Hence we have

\begin{align*} &z\frac{d}{dz}\left[bzJ_{\nu}(az)J_{\nu}'(bz)-azJ_{\nu}'(az)J_{\nu}(bz)\right]\\[2.5mm] &{}\hspace{10mm}{}=bzJ_{\nu}(az)J_{\nu}'(bz)+abz^2J_{\nu}'(az)J_{\nu}'(bz)+b^2z^2J_{\nu}(az)J_{\nu}''(bz) -azJ_{\nu}'(az)J_{\nu}(bz)-abz^2J_{\nu}'(az)J_{\nu}'(bz)-a^2z^2J_{\nu}''(az)J_{\nu}(bz)\\[2.5mm] &{}\hspace{10mm}{}=\left(a^2z^2-\nu^2\right)J_{\nu}(az)J_{\nu}(bz)-\left(b^2z^2-\nu^2\right)J_{\nu}(az)J_{\nu}(bz) =(a^2-b^2)z^2J_{\nu}(az)J_{\nu}(bz). \end{align*}

This implies that

\[\frac{d}{dz}\left[bzJ_{\nu}(az)J_{\nu}'(bz)-azJ_{\nu}'(az)J_{\nu}(bz)\right]=(a^2-b^2)zJ_{\nu}(az)J_{\nu}(bz),\]

which proves the lemma.

Theorem: For \(\nu\geq-1\) the Bessel function \(J_{\nu}(z)\) only has real zeros.

Proof: Since \(\nu\in\mathbb{R}\) we have: if \(z_0\in\mathbb{C}\) is a zero of \(J_{\nu}(z)\), so is \(\overline{z_0}\). Now we apply (3) with \(z=1\), \(a=z_0\) and \(b=\overline{z_0}\) to find that

\[0=(z_0^2-\overline{z_0}^2)\int_0^1tJ_{\nu}(z_0t)J_{\nu}(\overline{z_0}t)\,dt =(z_0^2-\overline{z_0}^2)\int_0^1t\left|J_{\nu}(z_0t)\right|^2\,dt.\]

This implies that \(z_0^2=\overline{z_0}^2\), which can only be true if \(z_0=x\in\mathbb{R}\) or \(z_0=iy\) with \(y\in\mathbb{R}\). Note that for \(z=iy\) with \(y\in\mathbb{R}\) we have

\[\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(\nu+k+1)\,k!}\left(\frac{z}{2}\right)^{2k} =\sum_{k=0}^{\infty}\frac{1}{\Gamma(\nu+k+1)\,k!}\left(\frac{y}{2}\right)^{2k}>0\]

for \(\nu>-1\). This implies that \(J_{\nu}(z)\) only has real zeros for \(\nu>-1\). For \(\nu=-1\) we have \(J_{-1}(z)=-J_1(z)\), which implies that the theorem also holds for \(\nu=-1\).

Theorem: For \(\nu\geq0\) the derivative \(J_{\nu}'(z)\) of the Bessel function only has real zeros.

Proof: Since \(\nu\in\mathbb{R}\) we have: if \(z_0\in\mathbb{C}\) is a zero of \(J_{\nu}'(z)\), so is \(\overline{z_0}\). As before (3) implies that \(z_0=x\in\mathbb{R}\) or \(z_0=iy\) with \(y\in\mathbb{R}\). Note that for \(z=iy\) with \(y\in\mathbb{R}\) we have

\[\sum_{k=0}^{\infty}\frac{(-1)^k\left(\frac{\nu}{2}+k\right)}{\Gamma(\nu+k+1)\,k!} \left(\frac{z}{2}\right)^{2k}=\sum_{k=0}^{\infty}\frac{\frac{\nu}{2}+k}{\Gamma(\nu+k+1)\,k!}\left(\frac{y}{2}\right)^{2k}>0\]

for \(\nu\geq0\).

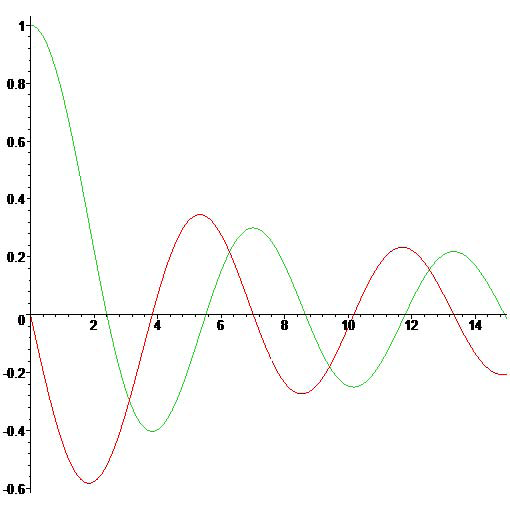
The Bessel function \(J_0(x)\) and its derivative \(J_0'(x)\).

Theorem: Both \(J_{\nu}(z)\) and \(J_{\nu}'(z)\) have infinitely many positive zeros.

Proof: Since all positive zeros of \(J_{\nu}(z)\) are simple, this follows from the asymptotic behaviour

\[J_{\nu}(z)\sim\sqrt{\frac{2}{\pi z}}\,\cos\left(z-\frac{\pi\nu}{2}-\frac{\pi}{4}\right), \quad |z|\rightarrow\infty\quad\text{with}\quad\left|\arg(z)\right|\le\pi-\delta<\pi.\]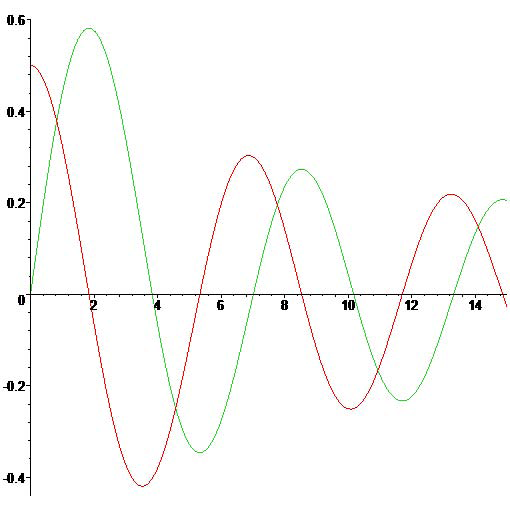

The Bessel function \(J_1(x)\) and its derivative \(J_1'(x)\).

---

Last modified on September 30, 2021