Speciale Functies – Besselfuncties – Nulpunten
De Besselfunctie \(J_{\nu}(z)\) van de eerste soort van orde \(\nu\in\mathbb{R}\) kan geschreven worden als
\[J_{\nu}(z)=\left(\frac{z}{2}\right)^{\nu}\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(\nu+k+1)\,k!}\left(\frac{z}{2}\right)^{2k}.\tag1\]Dit is een oplossing van de Bessel differentiaalvergelijking die kan worden geschreven als
\[z^2y''(z)+zy'(z)+(z^2-\nu^2)y(z)=0,\quad\nu\in\mathbb{R}.\tag2\]We gaan enkele basiseigenschappen van de nulpunten van de Besselfunctie \(J_{\nu}(z)\) en haar afgeleide \(J_{\nu}'(z)\) afleiden. Er geldt
Stelling: Alle nulpunten van \(J_{\nu}(z)\), behalve eventueel \(z=0\), zijn enkelvoudig.
Bewijs: Als \(z_0\neq0\) een meervoudig nulpunt is van \(J_{\nu}(z)\), dan geldt dat \(J_{\nu}(z_0)=0\) en \(J_{\nu}'(z_0)=0\). Omdat \(z_0\ne 0\) volgt uit de differentiaalvergelijking (2) dat ook \(J_{\nu}''(z_0)=0\). Iteratie leidt tot \(J_{\nu}^{(n)}(z_0)=0\) voor alle \(n\in\{0,1,2,\ldots\}\), waaruit volgt dat \(J_{\nu}(z)\) identiek gelijk aan nul is. Dat is een triviale contradictie.
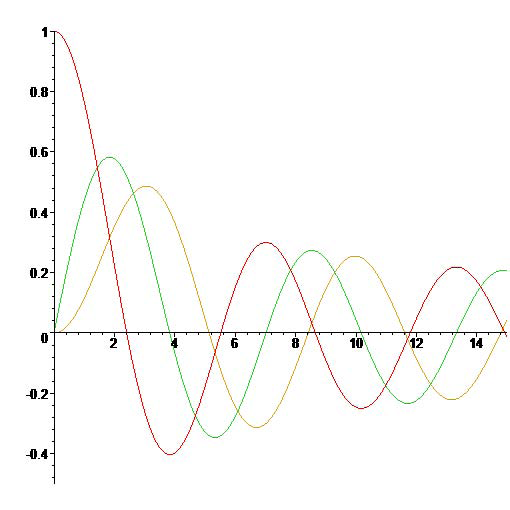
De Besselfuncties \(J_0(x)\), \(J_1(x)\) en \(J_2(x)\).
Stelling: Alle nulpunten van \(J_{\nu}'(z)\), behalve eventueel \(z=0\) of \(z=\pm\nu\), zijn enkelvoudig.
Bewijs: Als \(z_0\) een meervoudig nulpunt is van \(J_{\nu}'(z)\), dan geldt dat \(J_{\nu}'(z_0)=0\) en \(J_{\nu}''(z_0)=0\). Voor \(z_0\neq0\) en \(z_0\neq\pm\nu\) volgt dan uit de differentiaalvergelijking (2) dat ook \(J_{\nu}(z_0)=0\). Hieruit volgt weer dat \(J_{\nu}(z)\) identiek gelijk aan nul moet zijn, hetgeen duidelijk niet waar is.
Stelling: Als \(z_0\in\mathbb{C}\) een nulpunt is van \(J_{\nu}(z)\), dan ook \(-z_0\) en \(\pm\overline{z_0}\).
Bewijs: Omdat dit triviaal is voor \(z_0=0\) nemen we nu aan dat \(z_0\neq0\). Dan volgt uit (1) dat \(z_0\) een nulpunt is van
\[\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(\nu+k+1)\,k!}\left(\frac{z}{2}\right)^{2k}.\]Deze reeks is even en heeft reële coëfficiënten. Hieruit volgt dat \(-z_0\) en \(\pm\overline{z_0}\) ook nulpunten zijn.
Stelling: Als \(z_0\in\mathbb{C}\) een nulpunt is van \(J_{\nu}'(z)\), dan ook \(-z_0\) en \(\pm\overline{z_0}\).
Bewijs: Uit (1) volgt dat
\[J_{\nu}'(z)=\left(\frac{z}{2}\right)^{\nu-1}\sum_{k=0}^{\infty}\frac{(-1)^k\left(\frac{\nu}{2}+k\right)}{\Gamma(\nu+k+1)\,k!} \left(\frac{z}{2}\right)^{2k}.\]Dus, als \(z_0\neq0\) een nulpunt is van \(J_{\nu}'(z)\), dan moet het nulpunt zijn van
\[\sum_{k=0}^{\infty}\frac{(-1)^k\left(\frac{\nu}{2}+k\right)}{\Gamma(\nu+k+1)\,k!}\left(\frac{z}{2}\right)^{2k},\]dat even is en ook reële coëfficiënten heeft. Hieruit volgt dat \(-z_0\) en \(\pm\overline{z_0}\) ook nulpunten zijn.
Lemma: Voor \(\nu>-1\) geldt
\[(a^2-b^2)\int_0^ztJ_{\nu}(at)J_{\nu}(bt)\,dt=z\left[bJ_{\nu}(az)J_{\nu}'(bz)-aJ_{\nu}'(az)J_{\nu}(bz)\right].\tag3\]Bewijs: Uit de differentiaalvergelijking (2) volgt dat
\[c^2z^2J_{\nu}''(cz)+czJ_{\nu}'(cz)+\left(c^2z^2-\nu^2\right)J_{\nu}(cz)=0,\quad c\in\mathbb{C}.\]Dus geldt
\begin{align*} &z\frac{d}{dz}\left[bzJ_{\nu}(az)J_{\nu}'(bz)-azJ_{\nu}'(az)J_{\nu}(bz)\right]\\[2.5mm] &{}\hspace{10mm}{}=bzJ_{\nu}(az)J_{\nu}'(bz)+abz^2J_{\nu}'(az)J_{\nu}'(bz)+b^2z^2J_{\nu}(az)J_{\nu}''(bz) -azJ_{\nu}'(az)J_{\nu}(bz)-abz^2J_{\nu}'(az)J_{\nu}'(bz)-a^2z^2J_{\nu}''(az)J_{\nu}(bz)\\[2.5mm] &{}\hspace{10mm}{}=\left(a^2z^2-\nu^2\right)J_{\nu}(az)J_{\nu}(bz)-\left(b^2z^2-\nu^2\right)J_{\nu}(az)J_{\nu}(bz) =(a^2-b^2)z^2J_{\nu}(az)J_{\nu}(bz). \end{align*}Hieruit volgt dat
\[\frac{d}{dz}\left[bzJ_{\nu}(az)J_{\nu}'(bz)-azJ_{\nu}'(az)J_{\nu}(bz)\right]=(a^2-b^2)zJ_{\nu}(az)J_{\nu}(bz),\]hetgeen het lemma bewijst.
Stelling: Voor \(\nu\geq-1\) heeft de Besselfunctie \(J_{\nu}(z)\) alleen reële nulpunten.
Bewijs: Omdat \(\nu\in\mathbb{R}\) geldt: als \(z_0\in\mathbb{C}\) een nulpunt is van \(J_{\nu}(z)\), dan is \(\overline{z_0}\) dat ook. Nu passen we (3) toe met \(z=1\), \(a=z_0\) en \(b=\overline{z_0}\), dan volgt dat
\[0=(z_0^2-\overline{z_0}^2)\int_0^1tJ_{\nu}(z_0t)J_{\nu}(\overline{z_0}t)\,dt =(z_0^2-\overline{z_0}^2)\int_0^1t\left|J_{\nu}(z_0t)\right|^2\,dt.\]Hieruit volgt dat \(z_0^2=\overline{z_0}^2\), maar dat kan alleen waar zijn als \(z_0=x\in\mathbb{R}\) of \(z_0=iy\) met \(y\in\mathbb{R}\). Merk op dat voor \(z=iy\) met \(y\in\mathbb{R}\) geldt
\[\sum_{k=0}^{\infty}\frac{(-1)^k}{\Gamma(\nu+k+1)\,k!}\left(\frac{z}{2}\right)^{2k} =\sum_{k=0}^{\infty}\frac{1}{\Gamma(\nu+k+1)\,k!}\left(\frac{y}{2}\right)^{2k}>0\]voor \(\nu>-1\). Hieruit volgt dat \(J_{\nu}(z)\) alleen reële nulpunten heeft voor \(\nu>-1\). Voor \(\nu=-1\) geldt \(J_{-1}(z)=-J_1(z)\), waaruit volgt dat de stelling ook geldt voor \(\nu=-1\).
Stelling: Voor \(\nu\geq0\) heeft de afgeleide \(J_{\nu}'(z)\) van de Besselfunctie alleen reële nulpunten.
Bewijs: Omdat \(\nu\in\mathbb{R}\) geldt: als \(z_0\in\mathbb{C}\) een nulpunt is van \(J_{\nu}'(z)\), dan ook \(\overline{z_0}\). Dan volgt weer uit (3) dat \(z_0=x\in\mathbb{R}\) of \(z_0=iy\) met \(y\in\mathbb{R}\). Merk op dat voor \(z=iy\) met \(y\in\mathbb{R}\) geldt
\[\sum_{k=0}^{\infty}\frac{(-1)^k\left(\frac{\nu}{2}+k\right)}{\Gamma(\nu+k+1)\,k!} \left(\frac{z}{2}\right)^{2k}=\sum_{k=0}^{\infty}\frac{\frac{\nu}{2}+k}{\Gamma(\nu+k+1)\,k!}\left(\frac{y}{2}\right)^{2k}>0\]voor \(\nu\geq0\).
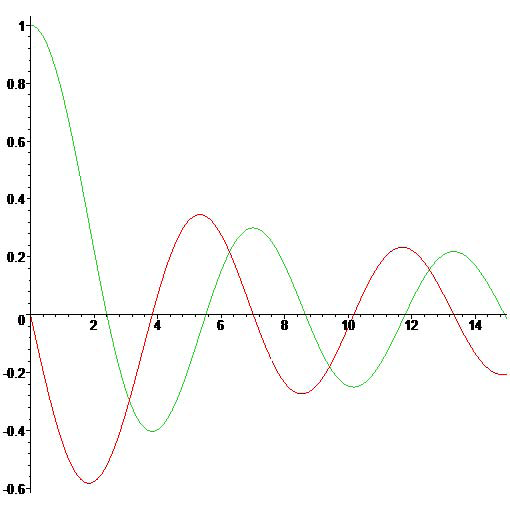
De Besselfunctie \(J_0(x)\) en haar afgeleide \(J_0'(x)\).
Stelling: Zowel \(J_{\nu}(z)\) als \(J_{\nu}'(z)\) hebben oneindig veel nulpunten.
Bewijs: Omdat alle positieve nulpunten van \(J_{\nu}(z)\) enkelvoduig zijn, volgt dit uit het asymptotische gedrag
\[J_{\nu}(z)\sim\sqrt{\frac{2}{\pi z}}\,\cos\left(z-\frac{\pi\nu}{2}-\frac{\pi}{4}\right), \quad |z|\rightarrow\infty\quad\text{met}\quad\left|\arg(z)\right|\le\pi-\delta<\pi.\]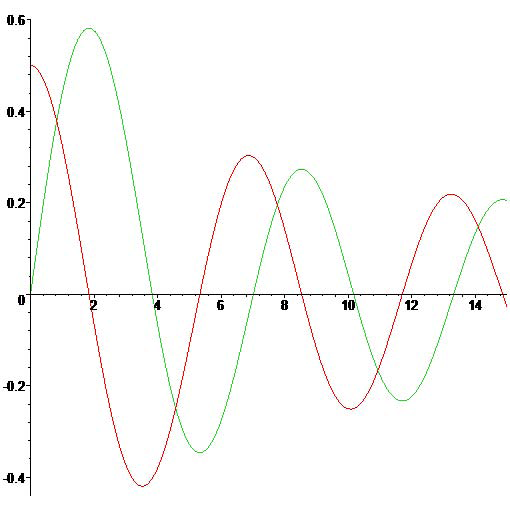
De Besselfunctie \(J_1(x)\) en haar afgeleide \(J_1'(x)\).
Last modified on 30 september 2021
 Onderwijs
Onderwijs

