Differential equations – Laplace transform – Impulse functions

The Dirac delta function

First we define for \(\tau>0\): \(d_{\tau}(t)=\left\{\begin{array}{ll}1/2\tau,&-\tau < t < \tau\\[2.5mm]0,&t\leq-\tau\;\text{or}\;t\geq\tau.\end{array}\right.\)

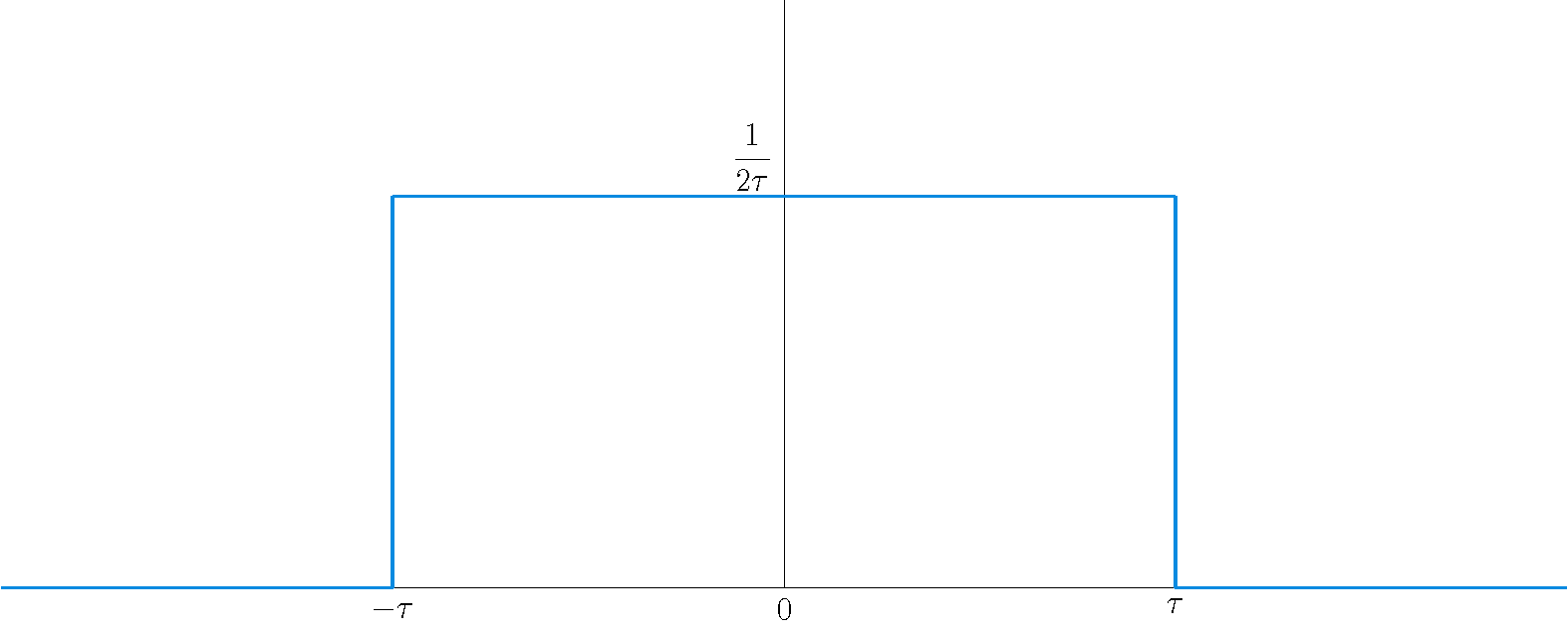
This function has the property that \(\displaystyle\int_{-\infty}^{\infty}d_{\tau}(t)\,dt=1\) for all \(\tau > 0\). Now we consider the "function" \(\delta(t):=\lim\limits_{\tau\downarrow0}d_{\tau}(t)\), which has the properties that \(\delta(t)=0\) for \(t\neq0\) and \(\displaystyle\int_{-\infty}^{\infty}\delta(t)\,dt=1\). This Dirac delta function is sometimes called a distribution or a generalized function. More general:

Definition: \(\delta(t-t_0)=0\) for all \(t\neq t_0\) and \(\displaystyle\int_{-\infty}^{\infty}\delta(t-t_0)\,dt=1\).

In order to find its Laplace transform we define: \(d_{\tau}(t-t_0)=\left\{\begin{array}{ll}1/2\tau,&t_0-\tau < t < t_0+\tau\\[2.5mm]0,&t\leq t_0-\tau\;\text{or}\;t\geq t_0+\tau.\end{array}\right.\)

We assume that \(\tau>0\), \(t_0>0\) and \(t_0-\tau>0\), so: \(t_0>\tau>0\). Then we have:

\[\mathcal{L}\{d_{\tau}(t-t_0)\}(s)=\int_0^{\infty}e^{-st}d_{\tau}(t-t_0)\,dt=\frac{1}{2\tau}\int_{t_0-\tau}^{t_0+\tau}e^{-st}\,dt =-\frac{1}{2s\tau}e^{-st}\bigg|_{t_0-\tau}^{t_0+\tau}=\frac{1}{2s\tau}\cdot e^{-st_0}\left(e^{s\tau}-e^{-s\tau}\right) =\frac{\sinh(s\tau)}{s\tau}\cdot e^{-st_0}.\]

Now we have: \(\displaystyle\lim\limits_{\tau\downarrow0}\frac{\sinh(s\tau)}{s\tau}=\lim\limits_{\tau\downarrow0}\frac{s\cosh(s\tau)}{s}=\cosh(0)=1\). This implies that:

\[\mathcal{L}\{\delta(t-t_0)\}(s)=\int_0^{\infty}e^{-st}\delta(t-t_0)\,dt=\lim\limits_{\tau\downarrow0}\int_0^{\infty}e^{-st}d_{\tau}(t-t_0)\,dt =\lim\limits_{\tau\downarrow0}\frac{\sinh(s\tau)}{s\tau}\cdot e^{-st_0}=e^{-st_0}.\]

So we have: \(\mathcal{L}\{\delta(t-t_0)\}(s)=e^{-st_0}\) for \(t_0>0\).

Now we consider \(\displaystyle\int_{-\infty}^{\infty}\delta(t-t_0)f(t)\,dt=\lim\limits_{\tau\downarrow0}\int_{-\infty}^{\infty}d_{\tau}(t-t_0)f(t)\,dt\). Now the mean value theorem implies that

\[\int_{-\infty}^{\infty}d_{\tau}(t-t_0)f(t)\,dt=\frac{1}{2\tau}\int_{t_0-\tau}^{t_0+\tau}f(t)\,dt=\frac{1}{2\tau}\cdot2\tau\cdot f(t^*)=f(t^*)\]

for certain \(t^*\) with \(t_0-\tau < t^* < t_0+\tau\). Note that for \(\tau\downarrow0\) we have: \(t^*\to t_0\). Hence: \(\displaystyle\int_{-\infty}^{\infty}\delta(t-t_0)f(t)\,dt=f(t_0)\). This implies that:

\[\mathcal{L}\{\delta(t-t_0)f(t)\}(s)=\int_0^{\infty}e^{-st}\delta(t-t_0)f(t)\,dt=f(t_0)e^{-st_0},\quad t_0>0,\quad s>0.\]

Examples:

1) If \(f(t)=\delta(t-\pi)\cos(t)\), then \(F(s)=\displaystyle\mathcal{L}\{f(t)\}(s)=\int_0^{\infty}e^{-st}\delta(t-\pi)\cos(t)\,dt=\cos(\pi)e^{-\pi s }=-e^{-\pi s}\).

2) If \(g(t)=\delta(t-2)e^{3t}\), then \(G(s)=\displaystyle\mathcal{L}\{g(t)\}(s)=\int_0^{\infty}e^{-st}\delta(t-2)e^{3t}\,dt=e^6e^{-2s}=e^{6-2s}\).

3) Consider \(y''(t)+4y(t)=\delta(t-\pi)\), \(y(0)=1\) and \(y'(0)=0\). Let \(Y(s)=\mathcal{L}\{y(t)\}(s)\) be the Laplace transform of \(y(t)\), then we have:

\[s^2Y(s)-sy(0)-y'(0)+4Y(s)=e^{-\pi s}\quad\Longrightarrow\quad (s^2+4)Y(s)=s+e^{-\pi s}.\]

Hence we have:

\[Y(s)=\frac{s}{s^2+4}+e^{-\pi s}\frac{1}{s^2+4}\quad\Longrightarrow\quad y(t)=\cos(2t)+\frac{1}{2}u_{\pi}(t)\sin(2t-2\pi).\]

---

Last modified on April 25, 2021