Differential equations – Laplace transform – Step functions
The Heaviside unit step function
Definition: For \(c\geq0\) we have: \(u_c(t)=\left\{\begin{array}{ll}0,&t < c\\[2.5mm]1,&t \geq c.\end{array}\right.\)
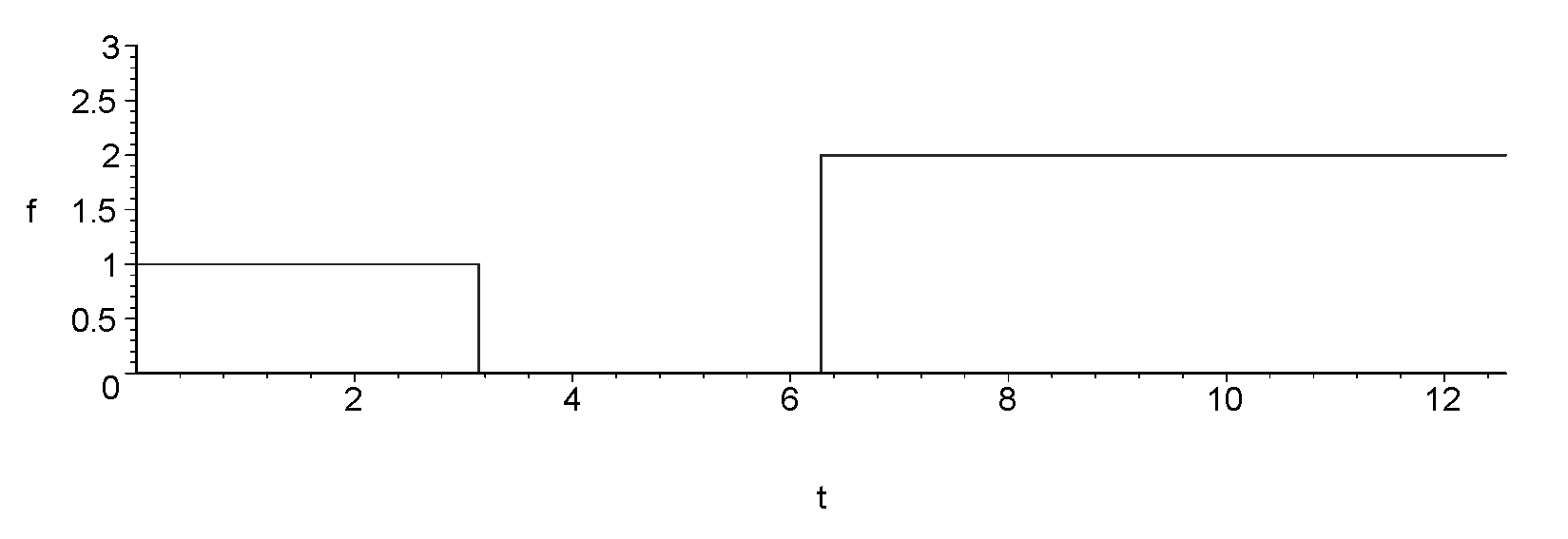
Example: \(f(t)=1-u_{\pi}(t)+2u_{2\pi}(t)=\left\{\begin{array}{ll}1-0+0=1,&t < \pi\\[2.5mm] 1-1+0=0,&\pi \leq t < 2\pi\\[2.5mm]1-1+2=2,&t \geq 2\pi.\end{array}\right.\)
For \(s>0\) we obtain:
\[\mathcal{L}\{u_c(t)\}(s)=\int_0^{\infty}e^{-st}u_c(t)\,dt=\int_c^{\infty}e^{-st}\,dt=-\frac{1}{s}e^{-st}\bigg|_c^{\infty}=\frac{e^{-cs}}{s}.\]Furthermore, we have:
\[\mathcal{L}\{u_c(t)f(t-c)\}(s)=\int_0^{\infty}e^{-st}u_c(t)f(t-c)\,dt=\int_c^{\infty}e^{-st}f(t-c)\,dt=\int_0^{\infty}e^{-s(u+c)}f(u)\,du =-e^{-cs}\int_0^{\infty}e^{-us}f(u)\,du=e^{-cs}F(s).\]Examples:
1) Consider \(f(t)=\left\{\begin{array}{l}\sin(t),&0\leq t < \pi\\[2.5mm]\sin(t)+\cos(t),&t\geq\pi.\end{array}\right.\) Then we have:
\[f(t)=\sin(t)+u_{\pi}(t)\cos(t)=\sin(t)-u_{\pi}(t)\cos(t-\pi)\quad\Longrightarrow\quad F(s)=\frac{1}{s^2+1}-e^{-\pi s}\frac{s}{s^2+1}.\]2) If \(F(s)=\displaystyle\frac{1-e^{-\pi s}}{s^2}=\frac{1}{s^2}-e^{-\pi s}\frac{1}{s^2}\), then: \(f(t)=t-u_{\pi}(t)(t-\pi)=\left\{\begin{array}{ll}t-0=t,&t < \pi\\[2.5mm]t-(t-\pi)=\pi,&t \geq \pi.\end{array}\right.\)
3) Consider \(y''(t)+4y(t)=f(t)\), \(y(0)=1\) and \(y'(0)=1\), where \(f(t)\) is the function in the first example.
Let \(Y(s)=\mathcal{L}\{y(t)\}(s)\) be the Laplace transform of \(y(t)\), then we have:
\[s^2Y(s)-sy(0)-y'(0)+4Y(s)=\frac{1}{s^2+1}-e^{-\pi s}\frac{s}{s^2+1}\quad\Longrightarrow\quad(s^2+4)Y(s)=s+1+\frac{1}{s^2+1}-e^{-\pi s}\frac{s}{s^2+1}.\]Using partial fractions we obtain that \(\displaystyle\frac{1}{(s^2+1)(s^2+4)}=\frac{1}{3}\left(\frac{1}{s^2+1}-\frac{1}{s^2+4}\right)\). Hence we have:
\[Y(s)=\frac{s+1}{s^2+4}+\frac{1}{(s^2+1)(s^2+4)}-e^{-\pi s}\frac{s}{(s^2+1)(s^2+4)}=\frac{1}{3}\frac{1}{s^2+1}+\frac{s}{s^2+4}+\frac{2}{3}\frac{1}{s^2+4}-\frac{1}{3}e^{-\pi s}\left(\frac{s}{s^2+1}-\frac{s}{s^2+4}\right).\]This implies that the solution of the initial-value problem is:
\[y(t)=\frac{1}{3}\sin(t)+\cos(2t)+\frac{1}{3}\sin(2t)-\frac{1}{3}u_{\pi}(t)\left(\cos(t-\pi)-\cos(2t-2\pi)\right).\]Last modified on April 25, 2021
 Teaching
Teaching

