Differentiaalvergelijkingen – Laplacetransformatie – Impulsfuncties

De Dirac deltafunctie

Om te beginnen definiëren we voor \(\tau>0\): \(d_{\tau}(t)=\left\{\begin{array}{ll}1/2\tau,&-\tau < t < \tau\\[2.5mm]0,&t\leq-\tau\;\text{or}\;t\geq\tau.\end{array}\right.\)

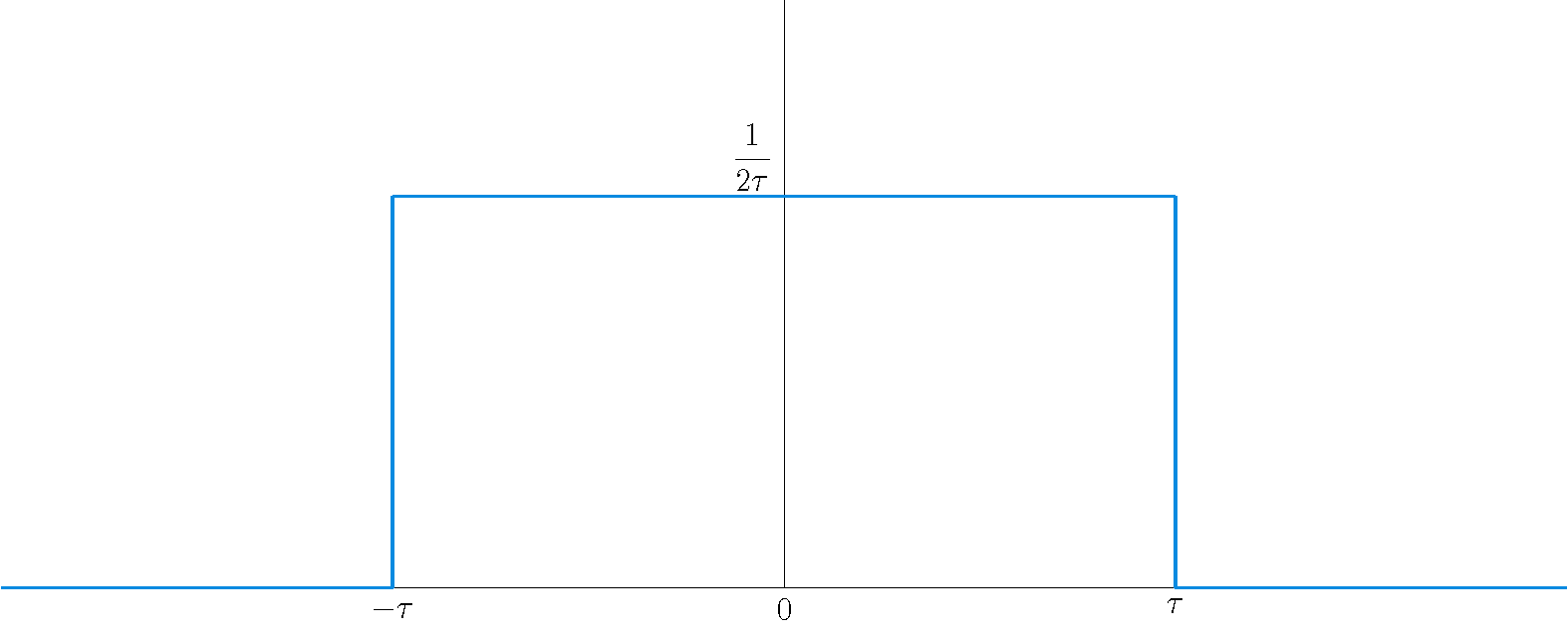
Deze functie heeft de eigenschap dat \(\displaystyle\int_{-\infty}^{\infty}d_{\tau}(t)\,dt=1\) voor alle \(\tau > 0\). Nu beschouwen we de "functie" \(\delta(t):=\lim\limits_{\tau\downarrow0}d_{\tau}(t)\), met de eigenschappen dat \(\delta(t)=0\) voor \(t\neq0\) en \(\displaystyle\int_{-\infty}^{\infty}\delta(t)\,dt=1\). Deze Dirac deltafunctie heet ook wel een distributie of een gegeneraliseerde functie. Algemener:

Definitie: \(\delta(t-t_0)=0\) voor alle \(t\neq t_0\) en \(\displaystyle\int_{-\infty}^{\infty}\delta(t-t_0)\,dt=1\).

Om hiervan de Laplacegetransformeerde te vinden definiëren we: \(d_{\tau}(t-t_0)=\left\{\begin{array}{ll}1/2\tau,&t_0-\tau < t < t_0+\tau\\[2.5mm]0,&t\leq t_0-\tau\;\text{or}\;t\geq t_0+\tau.\end{array}\right.\)

We nemen aan dat \(\tau>0\), \(t_0>0\) en \(t_0-\tau>0\), dus: \(t_0>\tau>0\). Dan geldt:

\[\mathcal{L}\{d_{\tau}(t-t_0)\}(s)=\int_0^{\infty}e^{-st}d_{\tau}(t-t_0)\,dt=\frac{1}{2\tau}\int_{t_0-\tau}^{t_0+\tau}e^{-st}\,dt =-\frac{1}{2s\tau}e^{-st}\bigg|_{t_0-\tau}^{t_0+\tau}=\frac{1}{2s\tau}\cdot e^{-st_0}\left(e^{s\tau}-e^{-s\tau}\right) =\frac{\sinh(s\tau)}{s\tau}\cdot e^{-st_0}.\]

Nu geldt: \(\displaystyle\lim\limits_{\tau\downarrow0}\frac{\sinh(s\tau)}{s\tau}=\lim\limits_{\tau\downarrow0}\frac{s\cosh(s\tau)}{s}=\cosh(0)=1\). Hieruit volgt dat:

\[\mathcal{L}\{\delta(t-t_0)\}(s)=\int_0^{\infty}e^{-st}\delta(t-t_0)\,dt=\lim\limits_{\tau\downarrow0}\int_0^{\infty}e^{-st}d_{\tau}(t-t_0)\,dt =\lim\limits_{\tau\downarrow0}\frac{\sinh(s\tau)}{s\tau}\cdot e^{-st_0}=e^{-st_0}.\]

Dus geldt: \(\mathcal{L}\{\delta(t-t_0)\}(s)=e^{-st_0}\) voor \(t_0>0\).

Beschouw nu \(\displaystyle\int_{-\infty}^{\infty}\delta(t-t_0)f(t)\,dt=\lim\limits_{\tau\downarrow0}\int_{-\infty}^{\infty}d_{\tau}(t-t_0)f(t)\,dt\). Uit de middelwaardestelling volgt nu dat

\[\int_{-\infty}^{\infty}d_{\tau}(t-t_0)f(t)\,dt=\frac{1}{2\tau}\int_{t_0-\tau}^{t_0+\tau}f(t)\,dt=\frac{1}{2\tau}\cdot2\tau\cdot f(t^*)=f(t^*)\]

voor zekere \(t^*\) met \(t_0-\tau < t^* < t_0+\tau\). Merk op dat voor \(\tau\downarrow0\) geldt dat: \(t^*\to t_0\). Dus: \(\displaystyle\int_{-\infty}^{\infty}\delta(t-t_0)f(t)\,dt=f(t_0)\). Hieruit volgt dat:

\[\mathcal{L}\{\delta(t-t_0)f(t)\}(s)=\int_0^{\infty}e^{-st}\delta(t-t_0)f(t)\,dt=f(t_0)e^{-st_0},\quad t_0>0,\quad s>0.\]

Voorbeelden:

1) Als \(f(t)=\delta(t-\pi)\cos(t)\), dan is \(F(s)=\displaystyle\mathcal{L}\{f(t)\}(s)=\int_0^{\infty}e^{-st}\delta(t-\pi)\cos(t)\,dt=\cos(\pi)e^{-\pi s }=-e^{-\pi s}\).

2) Als \(g(t)=\delta(t-2)e^{3t}\), dan is \(G(s)=\displaystyle\mathcal{L}\{g(t)\}(s)=\int_0^{\infty}e^{-st}\delta(t-2)e^{3t}\,dt=e^6e^{-2s}=e^{6-2s}\).

3) Beschouw \(y''(t)+4y(t)=\delta(t-\pi)\), \(y(0)=1\) en \(y'(0)=0\). Laat \(Y(s)=\mathcal{L}\{y(t)\}(s)\) de Laplacegetrasnformeerde van \(y(t)\) zijn, dan volgt:

\[s^2Y(s)-sy(0)-y'(0)+4Y(s)=e^{-\pi s}\quad\Longrightarrow\quad (s^2+4)Y(s)=s+e^{-\pi s}.\]

Dus geldt:

\[Y(s)=\frac{s}{s^2+4}+e^{-\pi s}\frac{1}{s^2+4}\quad\Longrightarrow\quad y(t)=\cos(2t)+\frac{1}{2}u_{\pi}(t)\sin(2t-2\pi).\]

---

Laatst gewijzigd op 25 april 2021