Speciale Functies – Hypergeometrische functies – Integraalrepresentatie van Barnes

De Mellin getransformeerde van een functie wordt gegeven door

\[F(s):=\int_0^{\infty}x^{s-1}f(x)\,dx.\]

De inversieformule wordt gegeven door

\[f(x)=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}F(s)\,ds,\quad c>0.\]

Merk op dat de definitie van de gammafunctie,

\[\Gamma(s)=\int_0^{\infty}x^{s-1}e^{-x}\,dx,\quad\text{Re}(s)>0,\]

laat zien dat \(\Gamma(s)\) de Mellin getransformeerde is van \(e^{-x}\). De inversieformule geeft dan

\[e^{-x}=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}\Gamma(s)\,ds,\quad c>0.\]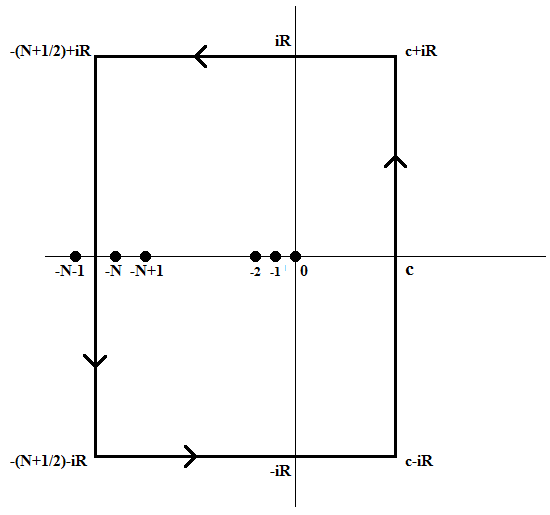

Dit kan rechtstreeks worden bewezen met behulp van de residustelling van Cauchy. Beschouw de rechthoekige contour \(\mathcal{C}\) met hoekpunten \(c\pm i R\) (\(c>0\)) en \(-(N+1/2)\pm i R\) met \(N\) een positief geheel getal. Dan bevinden de polen van \(\Gamma(s)\) binnen deze contour zich in \(0,-1,-2,\ldots,-N\) met residuen \((-1)^j/j!\) voor \(j=0,1,2,\ldots,N\) respectievelijk. Dus volgt uit de residustelling van Cauchy dat

\[\frac{1}{2\pi i}\int_{\mathcal{C}}x^{-s}\Gamma(s)\,ds=\sum_{j=0}^N\frac{(-1)^j}{j!}x^j.\]

Nu laten we \(R\) en \(N\) naar oneindig gaan. Uit de asymptotische formule van Stirling voor de gammafunctie volgt dan dat de integraal over \(\mathcal{C}\) minus het lijnstuk van \(c-iR\) naar \(c+iR\) naar nul gaat. Dus geldt

\[\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}\Gamma(s)\,ds=\lim\limits_{N\to\infty}\sum_{j=0}^N\frac{(-1)^j}{j!}x^j =\sum_{j=0}^{\infty}\frac{(-x)^j}{j!}=e^{-x}.\]

Een ander voorbeeld van een Mellin getransformeerde is:

\[B(s,t)=\int_0^1x^{s-1}(1-x)^{t-1}\,dx,\quad\text{Re}(s)>0,\quad\text{Re}(t)>0.\]

Hieruit volgt dat de betafunctie \(B(s,t)\) de Mellin getransformeerde is van de functie

\[f(x):=\left\{\begin{array}{ll}(1-x)^{t-1}, & 0 < x < 1\\[2.5mm]0, & x\geq 1.\end{array}\right.\]

De inversieformule geeft dan

\[f(x)=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}B(s,t)\,ds =\frac{\Gamma(t)}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}\frac{\Gamma(s)}{\Gamma(s+t)}\,ds,\quad\text{Re}(t)>0,\quad c>0.\]

Een andere representatie van de betafunctie is:

\[B(s,t)=\int_0^{\infty}\frac{x^{s-1}}{(1+x)^{s+t}}\,dx,\quad\text{Re}(s)>0,\quad\text{Re}(t)>0.\]

Hieruit volgt dat de betafunctie \(B(s,t-s)\) de Mellin getransformeerde is van de functie

\[g(x)=\frac{1}{(1+x)^t}.\]

De inversieformule geeft dan

\[\frac{1}{(1+x)^t}=g(x)=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}B(s,t-s)\,ds =\frac{1}{2\pi i}\,\frac{1}{\Gamma(t)}\int_{c-i\infty}^{c+i\infty}x^{-s}\Gamma(s)\Gamma(t-s)\,ds,\quad 0 < c < \text{Re}(t).\]

Deze voorbeelden suggereren dat we ook een complexe integraalrepresentatie voor de hypergeometrische functie \({}_2F_1\) zouden kunnen vinden door de Mellin getransformeerde te bepalen:

\begin{align*} \int_0^{\infty}x^{s-1}{}_2F_1\left(\genfrac{}{}{0pt}{}{a,b}{c}\,;\,-x\right)\,dx &=\int_0^{\infty}x^{s-1}\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\int_0^1t^{b-1}(1-t)^{c-b-1}(1+xt)^{-a}\,dt\,dx\\[2.5mm] &=\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\int_0^1t^{b-1}(1-t)^{c-b-1}\int_0^{\infty}\frac{x^{s-1}}{(1+xt)^a}\,dx\,dt. \end{align*}

Hierbij gebruikten we de integraalrepresentatie van Euler voor de \({}_2F_1\). De substitutie \(xt=u\) geeft nu

\[\int_0^{\infty}\frac{x^{s-1}}{(1+xt)^a}\,dx=t^{-s}\int_0^{\infty}\frac{u^{s-1}}{(1+u)^a}\,du =t^{-s}\,B(s,a-s)=t^{-s}\,\frac{\Gamma(s)\Gamma(a-s)}{\Gamma(a)}.\]

Dus geldt

\begin{align*} \int_0^{\infty}x^{s-1}{}_2F_1\left(\genfrac{}{}{0pt}{}{a,b}{c}\,;\,-x\right)\,dx &=\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\,\frac{\Gamma(s)\Gamma(a-s)}{\Gamma(a)}\int_0^1t^{b-s-1}(1-t)^{c-b-1}\,dt =\frac{\Gamma(c)\Gamma(s)\Gamma(a-s)}{\Gamma(b)\Gamma(c-b)\Gamma(a)}\,B(b-s,c-b)\\[2.5mm] &=\frac{\Gamma(c)\Gamma(s)\Gamma(a-s)}{\Gamma(b)\Gamma(c-b)\Gamma(a)}\,\frac{\Gamma(b-s)\Gamma(c-b)}{\Gamma(c-s)} =\frac{\Gamma(c)}{\Gamma(a)\Gamma(b)}\,\frac{\Gamma(s)\Gamma(a-s)\Gamma(b-s)}{\Gamma(c-s)}. \end{align*}

Hier hebben we aangenomen dat \(\min\left(\text{Re}(a),\text{Re}(b)\right)>\text{Re}(s)>0\). Door de inversieformule voor de Mellin transformatie toe te passen, zouden we kunnen verwachten dat

\[\frac{\Gamma(a)\Gamma(b)}{\Gamma(c)}\,{}_2F_1\left(\genfrac{}{}{0pt}{}{a,b}{c}\,;\,x\right) =\frac{1}{2\pi i}\int_{k-i\infty}^{k+i\infty}\frac{\Gamma(s)\Gamma(a-s)\Gamma(b-s)}{\Gamma(c-s)}(-x)^{-s}\,ds\]

voor \(\min\left(\text{Re}(a),\text{Re}(b)\right)>k>0\) en \(c\ne 0,-1,-2,\ldots\).

Dit is feitelijk de integraalrepresentatie van Barnes voor de \({}_2F_1\) die gewoonlijk wordt geschreven als:

Stelling: \(\displaystyle\frac{\Gamma(a)\Gamma(b)}{\Gamma(c)}\,{}_2F_1\left(\genfrac{}{}{0pt}{}{a,b}{c}\,;\,z\right) =\frac{1}{2\pi i}\int_{-i\infty}^{i\infty}\frac{\Gamma(a+s)\Gamma(b+s)\Gamma(-s)}{\Gamma(c+s)}(-z)^s\,ds,\quad|\arg(-z)|<\pi\).

Het pad van integratie is, zonodig, gekromd om de polen \(s=-a-n\) en \(s=-b-n\) te scheiden van de polen \(s=n\) met \(n\in\{0,1,2,\ldots\}\). Zo'n contour bestaat altijd als \(a\) en \(b\) geen negatieve gehele getallen zijn.

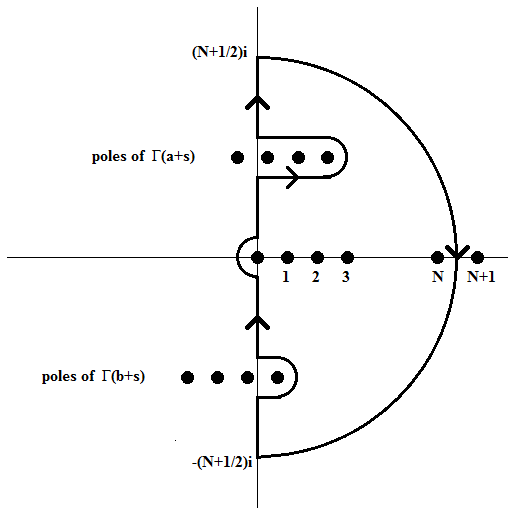
Bewijs: Laat \(\mathcal{C}\) de gesloten contour zijn gevormd door een deel van de kromme genoemd in de stelling van \(-(N+1/2)i\) naar \((N+1/2)i\) en de halve cirkel met straal \(N+1/2\) rechts van de imaginaire as met \(0\) als middelpunt. We tonen eerst aan dat bovenstaande integraal een analytische functie definieert voor \(|\arg(-z)|\le\pi-\delta\) met \(\delta>0\). Uit de reflectieformule van Euler en de asymptotische formule van Stirling voor de gammafunctie volgt voor de integrand:

\[\frac{\Gamma(a+s)\Gamma(b+s)\Gamma(-s)}{\Gamma(c+s)}(-z)^s =-\frac{\Gamma(a+s)\Gamma(b+s)}{\Gamma(c+s)\Gamma(1+s)}\,\frac{\pi}{\sin\pi s}\,(-z)^s\sim -s^{a+b-c-1}\frac{\pi}{\sin\pi s}\,(-z)^s.\]

Voor \(s=it\) geldt

\[-s^{a+b-c-1}\frac{\pi}{\sin\pi s}\,(-z)^s=-(it)^{a+b-c-1}\,2\pi i\, \frac{e^{it(\ln|z|+i\arg(-z))}}{e^{-\pi t}-e^{\pi t}}=\mathcal{O}(|t|^{a+b-c-1}e^{-|t|\delta})\]

voor \(|\arg(-z)|\le\pi-\delta\). Dit toont aan dat de integraal een analytische functie voorstelt in \(|\arg(-z)|\le\pi-\delta\) voor elke \(\delta>0\) en daaruit volgt dat deze analytisch is voor \(|\arg(-z)|<\pi\).

Op het deel van de contour \(\mathcal{C}\) op de halve cirkel is de integrand

\[\mathcal{O}(N^{a+b-c-1})\frac{(-z)^s}{\sin\pi s}\]

voor grote \(N\). Voor \(s=(N+1/2)e^{i\theta}\) en \(|z|<1\) geldt

\[\frac{(-z)^s}{\sin\pi s}=\mathcal{O}\left[e^{(N+1/2)(\cos\theta\,\ln|z|-\sin\theta\,\arg(-z)-\pi|\sin\theta|)}\right].\]

Omdat \(-\pi+\delta\le\arg(-z)\le\pi-\delta\), is de laatste uitdrukking

\[\mathcal{O}\left[e^{(N+1/2)(\cos\theta\,\ln|z|-\delta|\sin\theta|)}\right].\]

Nu geldt \(\cos\theta\ge\frac{1}{2}\sqrt{2}\) voor \(0\leq|\theta|\leq\pi/4\) en \(|\sin\theta|\ge\frac{1}{2}\sqrt{2}\) voor \(\pi/4\leq|\theta|\leq\pi/2\). Dus, omdat \(\ln|z|<0\), is de integrand

\[\left\{\begin{array}{ll}\mathcal{O}\left(N^{a+b-c-1}e^{\frac{1}{2}\sqrt{2}(N+1/2)\ln|z|}\right), & 0\leq|\theta|\leq\pi/4\\[2.5mm] \mathcal{O}\left(N^{a+b-c-1}e^{-\frac{1}{2}\sqrt{2}(N+1/2)\delta}\right), & \pi/4\leq|\theta|\leq\pi/2.\end{array}\right.\]

Hieruit volgt dat de integraal op de halve cirkel naar nul gaat voor \(N\to\infty\). Uit de residustelling volgt dan dat de integraal nadert naar de limiet van de sommen van de residuen in \(s=n\) met \(n\in\{0,1,2,\ldots\}\), dat wil zeggen

\[\sum_{n=0}^{\infty}\frac{\Gamma(a+n)\Gamma(b+n)}{\Gamma(c+n)\,n!}\,z^n =\frac{\Gamma(a)\Gamma(b)}{\Gamma(c)}\,\sum_{n=0}^{\infty}\frac{(a)_n(b)_n}{(c)_n}\frac{z^n}{n!} =\frac{\Gamma(a)\Gamma(b)}{\Gamma(c)}\,{}_2F_1\left(\genfrac{}{}{0pt}{}{a,b}{c}\,;\,z\right).\]

Dit bewijst de integraalrepresentatie van Barnes.

De Mellin transformatie heeft een convolutie-eigenschap, die we als volgt kunnen afleiden. Neem aan dat

\[F(s)=\int_0^{\infty}x^{s-1}f(x)\,dx\quad\text{en}\quad G(s)=\int_0^{\infty}x^{s-1}g(x)\,dx,\]

dan geldt

\[f(x)=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}F(s)x^{-s}\,ds\quad\text{en}\quad g(x)=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}G(s)x^{-s}\,ds.\]

Hieruit volgt dat

\begin{align*} \int_0^{\infty}x^{s-1}f(x)g(x)\,dx&=\frac{1}{2\pi i}\int_0^{\infty}x^{s-1}g(x)\left(\int_{c-i\infty}^{c+i\infty}F(t)x^{-t}\,dt\right)\,dx =\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}F(t)\left(\int_0^{\infty}x^{s-t-1}g(x)\,dx\right)\,dt\\[2.5mm] &=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}F(t)G(s-t)\,dt. \end{align*}

Als een toepassing beschouwen we

\[f(x)=\frac{x^b}{(1+x)^a}\quad\longleftrightarrow\quad F(s)=\frac{\Gamma(b+s)\Gamma(a-b-s)}{\Gamma(a)}\]

en

\[g(x)=\frac{x^d}{(1+x)^c}\quad\longleftrightarrow\quad G(s)=\frac{\Gamma(d+s)\Gamma(c-d-s)}{\Gamma(c)},\]

hetgeen leidt tot

\begin{align*} &\frac{1}{2\pi i}\int_{k-i\infty}^{k+i\infty}\frac{\Gamma(b+s)\Gamma(a-b-s)\Gamma(d+1-s)\Gamma(c-d-1+s)}{\Gamma(a)\Gamma(c)}\,ds =\frac{1}{2\pi i}\int_{k-i\infty}^{k+i\infty}F(s)G(1-s)\,ds=\int_0^{\infty}f(x)g(x)\,dx\\[2.5mm] &{}\hspace{25mm}{}=\int_0^{\infty}\frac{x^{b+d}}{(1+x)^{a+c}}\,dx=B(b+d+1,a+c-b-d-1)=\frac{\Gamma(b+d+1)\Gamma(a+c-b-d-1)}{\Gamma(a+c)} \end{align*}

voor een geschikte \(k\). Door hernoemen van de parameters, kan dit worden geschreven als

\[\frac{1}{2\pi i}\int_{-i\infty}^{i\infty}\Gamma(a+s)\Gamma(b+s)\Gamma(c-s)\Gamma(d-s)\,ds =\frac{\Gamma(a+c)\Gamma(a+d)\Gamma(b+c)\Gamma(b+d)}{\Gamma(a+b+c+d)},\]

geldig voor \(\text{Re}(a)>0\), \(\text{Re}(b)>0\), \(\text{Re}(c)>0\) en \(\text{Re}(d)>0\), kortom voor \(\text{Re}(a,b,c,d)>0\). Deze integraal heet de Mellin-Barnes integraal. Meer algemeen geldt

Stelling: Als het pad van integratie zodanig gekromd is dat de polen van \(\Gamma(a+s)\Gamma(b+s)\) gescheiden zijn van de polen van \(\Gamma(c-s)\Gamma(d-s)\), dan geldt

\[\frac{1}{2\pi i}\int_{-i\infty}^{i\infty}\Gamma(a+s)\Gamma(b+s)\Gamma(c-s)\Gamma(d-s)\,ds =\frac{\Gamma(a+c)\Gamma(a+d)\Gamma(b+c)\Gamma(b+d)}{\Gamma(a+b+c+d)}.\]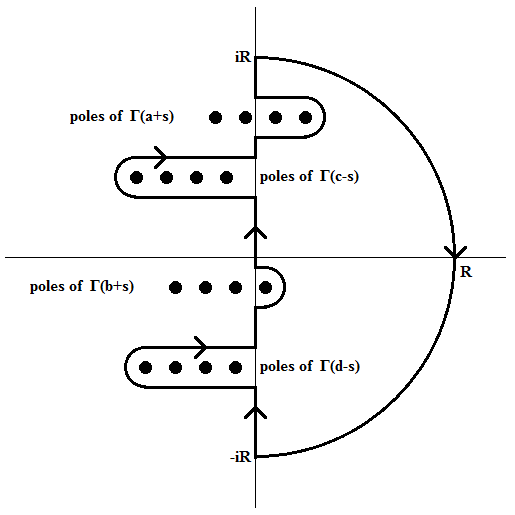

Bewijs: Weer gebruiken we de reflectieformule van Euler om de integrand te schrijven als

\[\frac{\Gamma(a+s)\Gamma(b+s)}{\Gamma(1-c+s)\Gamma(1-d+s)}\cdot\frac{\pi^2}{\sin\pi(c-s)\,\sin\pi(d-s)}.\]

Laat \(\mathcal{C}\) de gesloten contour zijn, gevormd door een deel van de kromme genoemd in de stelling van \(-iR\) naar \(iR\) en de halve cirkel met straal \(R\) rechts van de imaginaire as met \(0\) als middelpunt. Met behulp van de asymptotische formule van Stirling is de integrand

\[\mathcal{O}\left(s^{a+b+c+d-2}\,e^{-2\pi|\text{Im}\,s|}\right)\quad\text{voor}\quad|s|\to\infty\quad\text{on}\quad\mathcal{C}.\]

Omdat \(\text{Im}(s)\) willekeurig klein kan zijn als \(|s|\) groot is, nemen we aan dat \(\text{Re}(a+b+c+d)<1\) om te verzekeren dat de integraal op de halve cirkel naar nul gaat voor \(R\to\infty\). Dan volgt uit de residustelling van Cauchy (polen in \(s=c+n\) en \(s=d+n\) met \(n\in\{0,1,2,\ldots\}\) met residuen \((-1)^n/n!\)) dat de integraal gelijk is aan

\[\sum_{n=0}^{\infty}\Gamma(a+c+n)\Gamma(b+c+n)\Gamma(d-c-n)\frac{(-1)^n}{n!} +\sum_{n=0}^{\infty}\Gamma(a+d+n)\Gamma(b+d+n)\Gamma(c-d-n)\frac{(-1)^n}{n!}.\]

Merk op dat voor \(n\in\{0,1,2,\ldots\}\) geldt

\[\Gamma(d-c-n)=\frac{\Gamma(d-c)}{(d-c-1)(d-c-2)\cdots(d-c-n)} =\frac{\Gamma(d-c)}{(-1)^n(1+c-d)(2+c-d)\cdots(n+c-d)}=\frac{\Gamma(d-c)}{(-1)^n(1+c-d)_n}.\]

Hieruit volgt dat de integraal gelijk is aan

\[\Gamma(a+c)\Gamma(b+c)\Gamma(d-c)\sum_{n=0}^{\infty}\frac{(a+c)_n(b+c)_n}{(1+c-d)_n\,n!} +\Gamma(a+d)\Gamma(b+d)\Gamma(c-d)\sum_{n=0}^{\infty}\frac{(a+d)_n(b+d)_n}{(1+d-c)_n\,n!}.\]

Uiteindelijk volgt met de sommatieformule van Gauss en de reflectieformule van Euler dat de integraal gelijk is aan

\begin{align*} &\Gamma(a+c)\Gamma(b+c)\Gamma(d-c){}_2F_1\left(\genfrac{}{}{0pt}{}{a+c,b+c}{1+c-d}\,;\,1\right) +\Gamma(a+d)\Gamma(b+d)\Gamma(c-d){}_2F_1\left(\genfrac{}{}{0pt}{}{a+d,b+d}{1+d-c}\,;\,1\right)\\[2.5mm] &{}\hspace{15mm}{}=\Gamma(a+c)\Gamma(b+c)\Gamma(d-c)\frac{\Gamma(1+c-d)\Gamma(1-a-b-c-d)}{\Gamma(1-a-d)\Gamma(1-b-d)}\\[2.5mm] &{}\hspace{30mm}{}+\Gamma(a+d)\Gamma(b+d)\Gamma(c-d)\frac{\Gamma(1+d-c)\Gamma(1-a-b-c-d)}{\Gamma(1-a-c)\Gamma(1-b-c)}\\[2.5mm] &{}\hspace{15mm}{}=\frac{\Gamma(a+c)\Gamma(b+c)\Gamma(a+d)\Gamma(b+d)}{\Gamma(a+b+c+d)}\frac{\pi}{\sin\pi(d-c)}\frac{\sin\pi(a+d)}{\pi} \frac{\sin\pi(b+d)}{\pi}\frac{\pi}{\sin\pi(a+b+c+d)}\\[2.5mm] &{}\hspace{30mm}{}+\frac{\Gamma(a+d)\Gamma(b+d)\Gamma(a+c)\Gamma(b+c)}{\Gamma(a+b+c+d)}\frac{\pi}{\sin\pi(c-d)}\frac{\sin\pi(a+c)}{\pi} \frac{\sin\pi(b+c)}{\pi}\frac{\pi}{\sin\pi(a+b+c+d)}\\[2.5mm] &{}\hspace{15mm}{}=\frac{\Gamma(a+c)\Gamma(a+d)\Gamma(b+c)\Gamma(b+d)}{\Gamma(a+b+c+d)}\frac{\sin\pi(a+c)\sin\pi(b+c)-\sin\pi(a+d)\sin\pi(b+d)}{\sin\pi(c-d)\sin\pi(a+b+c+d)}. \end{align*}

Met behulp van trigonometrische formules kan worden aangetoond dat

\[\frac{\sin\pi(a+c)\sin\pi(b+c)-\sin\pi(a+d)\sin\pi(b+d)}{\sin\pi(c-d)\sin\pi(a+b+c+d)}=1.\]

Dit bewijst de stelling voor \(\text{Re}(a+b+c+d)<1\). Deze voorwaarde kan worden weggelaten door middel van analytische voortzetting van de parameters.

Er is ook een integraalrepresentatie van Barnes-type voor de confluent hypergeometrische functie. Om deze representatie te vinden, bepalen we de Mellin getransformeerde. Met behulp van de transformatieformule van Kummer volgt

\[\int_0^{\infty}z^{s-1}{}_1F_1\left(\genfrac{}{}{0pt}{}{a}{c}\,;\,-z\right)\,dz =\int_0^{\infty}z^{s-1}e^{-z}{}_1F_1\left(\genfrac{}{}{0pt}{}{c-a}{c}\,;\,z\right)\,dz =\sum_{n=0}^{\infty}\frac{(c-a)_n}{(c)_n\,n!}\int_0^{\infty}e^{-z}z^{s+n-1}\,dz =\sum_{n=0}^{\infty}\frac{(c-a)_n}{(c)_n\,n!}\,\Gamma(s+n).\]

Nu geldt \(\Gamma(s+n)=\Gamma(s)\,(s)_n\) en met behulp van de sommatieformule van Gauss volgt

\[\sum_{n=0}^{\infty}\frac{(c-a)_n}{(c)_n\,n!}\,\Gamma(s+n)=\Gamma(s)\,{}_2F_1\left(\genfrac{}{}{0pt}{}{c-a,s}{c}\,;\,1\right) =\frac{\Gamma(c)}{\Gamma(a)}\,\frac{\Gamma(s)\Gamma(a-s)}{\Gamma(c-s)}.\]

Dit leidt tot

Stelling: \(\displaystyle\frac{\Gamma(a)}{\Gamma(c)}\,{}_1F_1\left(\genfrac{}{}{0pt}{}{a}{c}\,;\,z\right) =\frac{1}{2\pi i}\int_{-i\infty}^{i\infty}\frac{\Gamma(a+s)}{\Gamma(c+s)}\Gamma(-s)(-z)^s\,ds,\quad\left|\arg(-z)\right|<\pi/2\).

Het pad van integratie is hier, zonodig, gekromd om de polen \(s=-a-n\) te scheiden van de polen \(s=n\) met \(n\in\{0,1,2,\ldots\}\).

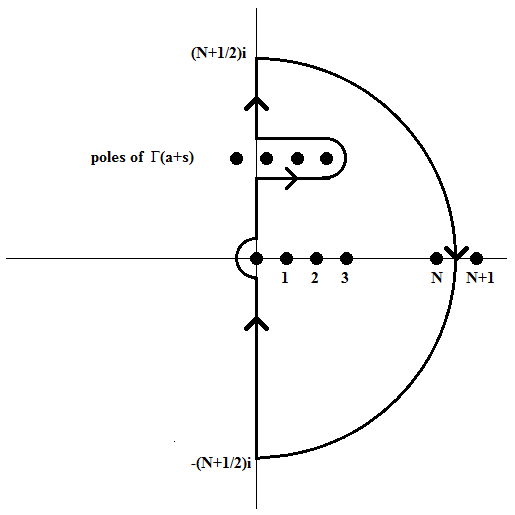
Bewijs: Het bewijs is vergelijkbaar met het bewijs van de integraalrepresentatie van Barnes voor de \({}_2F_1\) hypergeometrische functie. Toepassing van de residustelling van Cauchy geeft dan dat de integraal gelijk is aan de som van de residuen

\[\sum_{n=0}^{\infty}\frac{\Gamma(a+n)}{\Gamma(c+n)}\,\frac{(-1)^n}{n!}\,(-z)^n =\frac{\Gamma(a)}{\Gamma(c)}\,\sum_{n=0}^{\infty}\frac{(a)_n}{(c)_n}\,\frac{z^n}{n!} =\frac{\Gamma(a)}{\Gamma(c)}\,{}_1F_1\left(\genfrac{}{}{0pt}{}{a}{c}\,;\,z\right).\]

---

Last modified on 16 mei 2021