Special Functions – Hypergeometric functions – Barnes' integral representation

The Mellin transform of a function is given by

\[F(s):=\int_0^{\infty}x^{s-1}f(x)\,dx.\]

The inversion formula is given by

\[f(x)=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}F(s)\,ds,\quad c>0.\]

Note that the definition of the gamma function,

\[\Gamma(s)=\int_0^{\infty}x^{s-1}e^{-x}\,dx,\quad\text{Re}(s)>0,\]

implies that \(\Gamma(s)\) is the Mellin transform of \(e^{-x}\). The inversion formula reads

\[e^{-x}=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}\Gamma(s)\,ds,\quad c>0.\]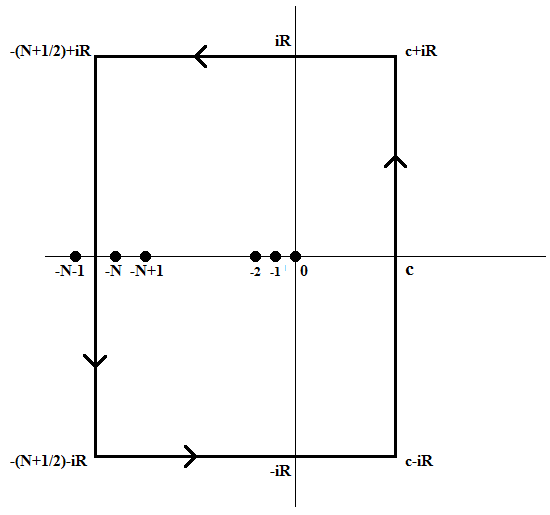

This can be proved directly by using Cauchy's residue theorem. Consider the rectangular contour \(\mathcal{C}\) with vertices \(c\pm i R\) (\(c>0\)) and \(-(N+1/2)\pm i R\), where \(N\) is a positive integer. Then the poles of \(\Gamma(s)\) inside this contour are at \(0,-1,-2,\ldots,-N\) with residues \((-1)^j/j!\) for \(j=0,1,2,\ldots,N\) respectively. Hence, Cauchy's residue theorem implies that

\[\frac{1}{2\pi i}\int_{\mathcal{C}}x^{-s}\Gamma(s)\,ds=\sum_{j=0}^N\frac{(-1)^j}{j!}x^j.\]

Now we let \(R\) and \(N\) tend to infinity. Then Stirling's asymptotic formula for the gamma function implies that the integral on \(\mathcal{C}\) minus the line joining \(c-iR\) and \(c+iR\) tends to zero. Hence we have

\[\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}\Gamma(s)\,ds=\lim\limits_{N\to\infty}\sum_{j=0}^N\frac{(-1)^j}{j!}x^j =\sum_{j=0}^{\infty}\frac{(-x)^j}{j!}=e^{-x}.\]

Another example of a Mellin transform is:

\[B(s,t)=\int_0^1x^{s-1}(1-x)^{t-1}\,dx,\quad\text{Re}(s)>0,\quad\text{Re}(t)>0.\]

This implies that the beta function \(B(s,t)\) is the Mellin transform of the function

\[f(x):=\left\{\begin{array}{ll}(1-x)^{t-1}, & 0 < x < 1\\[2.5mm]0, & x\geq 1.\end{array}\right.\]

The inversion formula then reads

\[f(x)=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}B(s,t)\,ds =\frac{\Gamma(t)}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}\frac{\Gamma(s)}{\Gamma(s+t)}\,ds,\quad\text{Re}(t)>0,\quad c>0.\]

Another representation of the beta function is:

\[B(s,t)=\int_0^{\infty}\frac{x^{s-1}}{(1+x)^{s+t}}\,dx,\quad\text{Re}(s)>0,\quad\text{Re}(t)>0.\]

This implies that the beta function \(B(s,t-s)\) is the Mellin transform of the function

\[g(x)=\frac{1}{(1+x)^t}.\]

The inversion formula then reads

\[\frac{1}{(1+x)^t}=g(x)=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}B(s,t-s)\,ds =\frac{1}{2\pi i}\,\frac{1}{\Gamma(t)}\int_{c-i\infty}^{c+i\infty}x^{-s}\Gamma(s)\Gamma(t-s)\,ds,\quad 0 < c < \text{Re}(t).\]

These examples suggest that we might obtain a complex integral representation for the hypergeometric function \({}_2F_1\) by finding its Mellin transform:

\begin{align*} \int_0^{\infty}x^{s-1}{}_2F_1\left(\genfrac{}{}{0pt}{}{a,b}{c}\,;\,-x\right)\,dx &=\int_0^{\infty}x^{s-1}\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\int_0^1t^{b-1}(1-t)^{c-b-1}(1+xt)^{-a}\,dt\,dx\\[2.5mm] &=\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\int_0^1t^{b-1}(1-t)^{c-b-1}\int_0^{\infty}\frac{x^{s-1}}{(1+xt)^a}\,dx\,dt. \end{align*}

Here we used Euler's integral representation for the \({}_2F_1\). The substitution \(xt=u\) now gives

\[\int_0^{\infty}\frac{x^{s-1}}{(1+xt)^a}\,dx=t^{-s}\int_0^{\infty}\frac{u^{s-1}}{(1+u)^a}\,du =t^{-s}\,B(s,a-s)=t^{-s}\,\frac{\Gamma(s)\Gamma(a-s)}{\Gamma(a)}.\]

Hence we have

\begin{align*} \int_0^{\infty}x^{s-1}{}_2F_1\left(\genfrac{}{}{0pt}{}{a,b}{c}\,;\,-x\right)\,dx &=\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\,\frac{\Gamma(s)\Gamma(a-s)}{\Gamma(a)}\int_0^1t^{b-s-1}(1-t)^{c-b-1}\,dt =\frac{\Gamma(c)\Gamma(s)\Gamma(a-s)}{\Gamma(b)\Gamma(c-b)\Gamma(a)}\,B(b-s,c-b)\\[2.5mm] &=\frac{\Gamma(c)\Gamma(s)\Gamma(a-s)}{\Gamma(b)\Gamma(c-b)\Gamma(a)}\,\frac{\Gamma(b-s)\Gamma(c-b)}{\Gamma(c-s)} =\frac{\Gamma(c)}{\Gamma(a)\Gamma(b)}\,\frac{\Gamma(s)\Gamma(a-s)\Gamma(b-s)}{\Gamma(c-s)}. \end{align*}

Here we assumed that \(\min\left(\text{Re}(a),\text{Re}(b)\right)>\text{Re}(s)>0\). Applying the inversion formula for the Mellin transform we might expect that

\[\frac{\Gamma(a)\Gamma(b)}{\Gamma(c)}\,{}_2F_1\left(\genfrac{}{}{0pt}{}{a,b}{c}\,;\,x\right) =\frac{1}{2\pi i}\int_{k-i\infty}^{k+i\infty}\frac{\Gamma(s)\Gamma(a-s)\Gamma(b-s)}{\Gamma(c-s)}(-x)^{-s}\,ds\]

for \(\min\left(\text{Re}(a),\text{Re}(b)\right)>k>0\) and \(c\ne 0,-1,-2,\ldots\).

In fact, this is Barnes' integral representation for the \({}_2F_1\) which is usually written as:

Theorem: \(\displaystyle\frac{\Gamma(a)\Gamma(b)}{\Gamma(c)}\,{}_2F_1\left(\genfrac{}{}{0pt}{}{a,b}{c}\,;\,z\right) =\frac{1}{2\pi i}\int_{-i\infty}^{i\infty}\frac{\Gamma(a+s)\Gamma(b+s)\Gamma(-s)}{\Gamma(c+s)}(-z)^s\,ds,\quad|\arg(-z)|<\pi\).

The path of integration is curved, if necessary, to separate the poles \(s=-a-n\) and \(s=-b-n\) from the poles \(s=n\) with \(n\in\{0,1,2,\ldots\}\). Such a contour always exists if \(a\) and \(b\) are not negative integers.

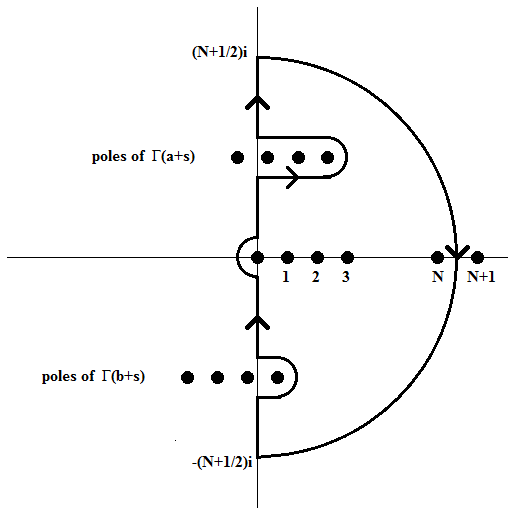
Proof: Let \(\mathcal{C}\) be the closed contour formed by a part of the curve used in the theorem from \(-(N+1/2)i\) to \((N+1/2)i\) together with the semicircle of radius \(N+1/2\) to the right of the imaginary axis with \(0\) as center. We first show that the above integral defines an analytic function for \(|\arg(-z)|\le\pi-\delta\) with \(\delta>0\). By using Euler's reflection formula and Stirling's asymptotic formula for the gamma function we find for the integrand:

\[\frac{\Gamma(a+s)\Gamma(b+s)\Gamma(-s)}{\Gamma(c+s)}(-z)^s =-\frac{\Gamma(a+s)\Gamma(b+s)}{\Gamma(c+s)\Gamma(1+s)}\,\frac{\pi}{\sin\pi s}\,(-z)^s\sim -s^{a+b-c-1}\frac{\pi}{\sin\pi s}\,(-z)^s.\]

For \(s=it\) we have

\[-s^{a+b-c-1}\frac{\pi}{\sin\pi s}\,(-z)^s=-(it)^{a+b-c-1}\,2\pi i\, \frac{e^{it(\ln|z|+i\arg(-z))}}{e^{-\pi t}-e^{\pi t}}=\mathcal{O}(|t|^{a+b-c-1}e^{-|t|\delta})\]

for \(|\arg(-z)|\le\pi-\delta\). This shows that the integral represents an analytic function in \(|\arg(-z)|\le\pi-\delta\) for every \(\delta>0\), which implies that it is analytic for \(|\arg(-z)|<\pi\).

On the semicircular part of the contour \(\mathcal{C}\) the integrand is

\[\mathcal{O}(N^{a+b-c-1})\frac{(-z)^s}{\sin\pi s}\]

for large \(N\). For \(s=(N+1/2)e^{i\theta}\) and \(|z|<1\) we have

\[\frac{(-z)^s}{\sin\pi s}=\mathcal{O}\left[e^{(N+1/2)(\cos\theta\,\ln|z|-\sin\theta\,\arg(-z)-\pi|\sin\theta|)}\right].\]

Since \(-\pi+\delta\le\arg(-z)\le\pi-\delta\), the last expression is

\[\mathcal{O}\left[e^{(N+1/2)(\cos\theta\,\ln|z|-\delta|\sin\theta|)}\right].\]

Now we have \(\cos\theta\ge\frac{1}{2}\sqrt{2}\) for \(0\leq|\theta|\leq\pi/4\) and \(|\sin\theta|\ge\frac{1}{2}\sqrt{2}\) for \(\pi/4\leq|\theta|\leq\pi/2\). Hence, since \(\ln|z|<0\), the integrand is

\[\left\{\begin{array}{ll}\mathcal{O}\left(N^{a+b-c-1}e^{\frac{1}{2}\sqrt{2}(N+1/2)\ln|z|}\right), & 0\leq|\theta|\leq\pi/4\\[2.5mm] \mathcal{O}\left(N^{a+b-c-1}e^{-\frac{1}{2}\sqrt{2}(N+1/2)\delta}\right), & \pi/4\leq|\theta|\leq\pi/2.\end{array}\right.\]

This implies that the integral on the semicircle tends to zero for \(N\to\infty\). The residue theorem then implies that the integral tends to the limit of the sums of the residues at \(s=n\) with \(n\in\{0,1,2,\ldots\}\), id est

\[\sum_{n=0}^{\infty}\frac{\Gamma(a+n)\Gamma(b+n)}{\Gamma(c+n)\,n!}\,z^n =\frac{\Gamma(a)\Gamma(b)}{\Gamma(c)}\,\sum_{n=0}^{\infty}\frac{(a)_n(b)_n}{(c)_n}\frac{z^n}{n!} =\frac{\Gamma(a)\Gamma(b)}{\Gamma(c)}\,{}_2F_1\left(\genfrac{}{}{0pt}{}{a,b}{c}\,;\,z\right).\]

This proves Barnes' integral representation.

The Mellin transform has a convolution property, which can be obtained as follows. Assume that

\[F(s)=\int_0^{\infty}x^{s-1}f(x)\,dx\quad\text{and}\quad G(s)=\int_0^{\infty}x^{s-1}g(x)\,dx,\]

then we have

\[f(x)=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}F(s)x^{-s}\,ds\quad\text{and}\quad g(x)=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}G(s)x^{-s}\,ds.\]

This implies that

\begin{align*} \int_0^{\infty}x^{s-1}f(x)g(x)\,dx&=\frac{1}{2\pi i}\int_0^{\infty}x^{s-1}g(x)\left(\int_{c-i\infty}^{c+i\infty}F(t)x^{-t}\,dt\right)\,dx =\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}F(t)\left(\int_0^{\infty}x^{s-t-1}g(x)\,dx\right)\,dt\\[2.5mm] &=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}F(t)G(s-t)\,dt. \end{align*}

As an application we consider

\[f(x)=\frac{x^b}{(1+x)^a}\quad\longleftrightarrow\quad F(s)=\frac{\Gamma(b+s)\Gamma(a-b-s)}{\Gamma(a)}\]

and

\[g(x)=\frac{x^d}{(1+x)^c}\quad\longleftrightarrow\quad G(s)=\frac{\Gamma(d+s)\Gamma(c-d-s)}{\Gamma(c)},\]

which leads to

\begin{align*} &\frac{1}{2\pi i}\int_{k-i\infty}^{k+i\infty}\frac{\Gamma(b+s)\Gamma(a-b-s)\Gamma(d+1-s)\Gamma(c-d-1+s)}{\Gamma(a)\Gamma(c)}\,ds =\frac{1}{2\pi i}\int_{k-i\infty}^{k+i\infty}F(s)G(1-s)\,ds=\int_0^{\infty}f(x)g(x)\,dx\\[2.5mm] &{}\hspace{25mm}{}=\int_0^{\infty}\frac{x^{b+d}}{(1+x)^{a+c}}\,dx=B(b+d+1,a+c-b-d-1)=\frac{\Gamma(b+d+1)\Gamma(a+c-b-d-1)}{\Gamma(a+c)} \end{align*}

for a suitable \(k\). By renaming the parameters, this can be written as

\[\frac{1}{2\pi i}\int_{-i\infty}^{i\infty}\Gamma(a+s)\Gamma(b+s)\Gamma(c-s)\Gamma(d-s)\,ds =\frac{\Gamma(a+c)\Gamma(a+d)\Gamma(b+c)\Gamma(b+d)}{\Gamma(a+b+c+d)},\]

which holds for \(\text{Re}(a)>0\), \(\text{Re}(b)>0\), \(\text{Re}(c)>0\) and \(\text{Re}(d)>0\), shortly for \(\text{Re}(a,b,c,d)>0\). This integral is called the Mellin-Barnes integral. More general we have

Theorem: If the path of integration is curved to separate the poles of \(\Gamma(a+s)\Gamma(b+s)\) from the poles of \(\Gamma(c-s)\Gamma(d-s)\), then we have

\[\frac{1}{2\pi i}\int_{-i\infty}^{i\infty}\Gamma(a+s)\Gamma(b+s)\Gamma(c-s)\Gamma(d-s)\,ds =\frac{\Gamma(a+c)\Gamma(a+d)\Gamma(b+c)\Gamma(b+d)}{\Gamma(a+b+c+d)}.\]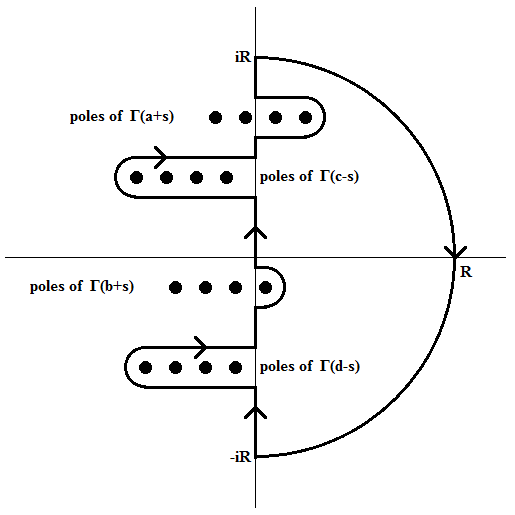

Proof: Again we use Euler's reflection formula to write the integrand as

\[\frac{\Gamma(a+s)\Gamma(b+s)}{\Gamma(1-c+s)\Gamma(1-d+s)}\cdot\frac{\pi^2}{\sin\pi(c-s)\,\sin\pi(d-s)}.\]

Let \(\mathcal{C}\) be the closed contour formed by a part of the curve used in the theorem from \(-iR\) to \(iR\) together with the semicircle of radius \(R\) to the right of the imaginary axis with \(0\) as center. By Stirling's asymptotic formula the integrand is

\[\mathcal{O}\left(s^{a+b+c+d-2}\,e^{-2\pi|\text{Im}\,s|}\right)\quad\text{for}\quad|s|\to\infty\quad\text{on}\quad\mathcal{C}.\]

Since \(\text{Im}(s)\) can be arbitrarily small when \(|s|\) is large, we assume that \(\text{Re}(a+b+c+d)<1\) to ensure that the integral on the semicircle tends to zero for \(R\to\infty\). Then, by Cauchy's residue theorem (poles in \(s=c+n\) and \(s=d+n\) with \(n\in\{0,1,2,\ldots\}\) with residues \((-1)^n/n!\)), the integral equals

\[\sum_{n=0}^{\infty}\Gamma(a+c+n)\Gamma(b+c+n)\Gamma(d-c-n)\frac{(-1)^n}{n!} +\sum_{n=0}^{\infty}\Gamma(a+d+n)\Gamma(b+d+n)\Gamma(c-d-n)\frac{(-1)^n}{n!}.\]

Note that for \(n\in\{0,1,2,\ldots\}\) we have

\[\Gamma(d-c-n)=\frac{\Gamma(d-c)}{(d-c-1)(d-c-2)\cdots(d-c-n)} =\frac{\Gamma(d-c)}{(-1)^n(1+c-d)(2+c-d)\cdots(n+c-d)}=\frac{\Gamma(d-c)}{(-1)^n(1+c-d)_n}.\]

This implies that the integral equals

\[\Gamma(a+c)\Gamma(b+c)\Gamma(d-c)\sum_{n=0}^{\infty}\frac{(a+c)_n(b+c)_n}{(1+c-d)_n\,n!} +\Gamma(a+d)\Gamma(b+d)\Gamma(c-d)\sum_{n=0}^{\infty}\frac{(a+d)_n(b+d)_n}{(1+d-c)_n\,n!}.\]

Finally we use Gauss's summation formula and Euler's reflection formula to find that the integral equals

\begin{align*} &\Gamma(a+c)\Gamma(b+c)\Gamma(d-c){}_2F_1\left(\genfrac{}{}{0pt}{}{a+c,b+c}{1+c-d}\,;\,1\right) +\Gamma(a+d)\Gamma(b+d)\Gamma(c-d){}_2F_1\left(\genfrac{}{}{0pt}{}{a+d,b+d}{1+d-c}\,;\,1\right)\\[2.5mm] &{}\hspace{15mm}{}=\Gamma(a+c)\Gamma(b+c)\Gamma(d-c)\frac{\Gamma(1+c-d)\Gamma(1-a-b-c-d)}{\Gamma(1-a-d)\Gamma(1-b-d)}\\[2.5mm] &{}\hspace{30mm}{}+\Gamma(a+d)\Gamma(b+d)\Gamma(c-d)\frac{\Gamma(1+d-c)\Gamma(1-a-b-c-d)}{\Gamma(1-a-c)\Gamma(1-b-c)}\\[2.5mm] &{}\hspace{15mm}{}=\frac{\Gamma(a+c)\Gamma(b+c)\Gamma(a+d)\Gamma(b+d)}{\Gamma(a+b+c+d)}\frac{\pi}{\sin\pi(d-c)}\frac{\sin\pi(a+d)}{\pi} \frac{\sin\pi(b+d)}{\pi}\frac{\pi}{\sin\pi(a+b+c+d)}\\[2.5mm] &{}\hspace{30mm}{}+\frac{\Gamma(a+d)\Gamma(b+d)\Gamma(a+c)\Gamma(b+c)}{\Gamma(a+b+c+d)}\frac{\pi}{\sin\pi(c-d)}\frac{\sin\pi(a+c)}{\pi} \frac{\sin\pi(b+c)}{\pi}\frac{\pi}{\sin\pi(a+b+c+d)}\\[2.5mm] &{}\hspace{15mm}{}=\frac{\Gamma(a+c)\Gamma(a+d)\Gamma(b+c)\Gamma(b+d)}{\Gamma(a+b+c+d)}\frac{\sin\pi(a+c)\sin\pi(b+c)-\sin\pi(a+d)\sin\pi(b+d)}{\sin\pi(c-d)\sin\pi(a+b+c+d)}. \end{align*}

By using trigonometric relations it can be shown that

\[\frac{\sin\pi(a+c)\sin\pi(b+c)-\sin\pi(a+d)\sin\pi(b+d)}{\sin\pi(c-d)\sin\pi(a+b+c+d)}=1.\]

This proves the theorem for \(\text{Re}(a+b+c+d)<1\). This condition can be removed by using analytic continuation of the parameters.

We also have a Barnes-type integral representation for the confluent hypergeometric function. In order to find this representation we evaluate its Mellin transform. By using Kummer's transformation formula we obtain

\[\int_0^{\infty}z^{s-1}{}_1F_1\left(\genfrac{}{}{0pt}{}{a}{c}\,;\,-z\right)\,dz =\int_0^{\infty}z^{s-1}e^{-z}{}_1F_1\left(\genfrac{}{}{0pt}{}{c-a}{c}\,;\,z\right)\,dz =\sum_{n=0}^{\infty}\frac{(c-a)_n}{(c)_n\,n!}\int_0^{\infty}e^{-z}z^{s+n-1}\,dz =\sum_{n=0}^{\infty}\frac{(c-a)_n}{(c)_n\,n!}\,\Gamma(s+n).\]

Now we have \(\Gamma(s+n)=\Gamma(s)\,(s)_n\) and by using Gauss's summation formula

\[\sum_{n=0}^{\infty}\frac{(c-a)_n}{(c)_n\,n!}\,\Gamma(s+n)=\Gamma(s)\,{}_2F_1\left(\genfrac{}{}{0pt}{}{c-a,s}{c}\,;\,1\right) =\frac{\Gamma(c)}{\Gamma(a)}\,\frac{\Gamma(s)\Gamma(a-s)}{\Gamma(c-s)}.\]

This leads to

Theorem: \(\displaystyle\frac{\Gamma(a)}{\Gamma(c)}\,{}_1F_1\left(\genfrac{}{}{0pt}{}{a}{c}\,;\,z\right) =\frac{1}{2\pi i}\int_{-i\infty}^{i\infty}\frac{\Gamma(a+s)}{\Gamma(c+s)}\Gamma(-s)(-z)^s\,ds,\quad\left|\arg(-z)\right|<\pi/2\).

Here the path of integration is curved, if necessary, to separate the poles \(s=-a-n\) from the poles \(s=n\) with \(n\in\{0,1,2,\ldots\}\).

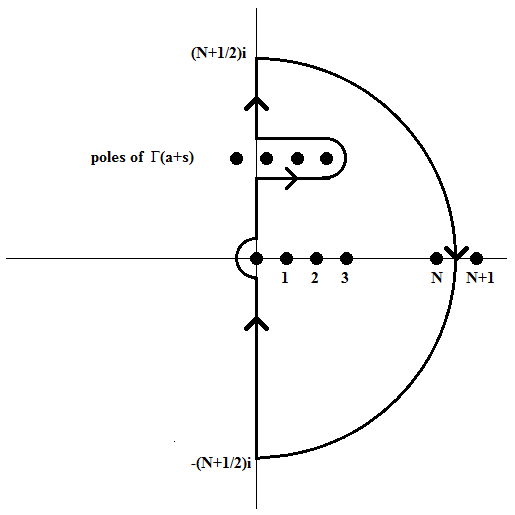
Proof: The proof is similar to the proof of Barnes' integral representation for the \({}_2F_1\) hypergeometric function. Application of Cauchy's residue theorem then gives that the integral equals the sum of residues

\[\sum_{n=0}^{\infty}\frac{\Gamma(a+n)}{\Gamma(c+n)}\,\frac{(-1)^n}{n!}\,(-z)^n =\frac{\Gamma(a)}{\Gamma(c)}\,\sum_{n=0}^{\infty}\frac{(a)_n}{(c)_n}\,\frac{z^n}{n!} =\frac{\Gamma(a)}{\Gamma(c)}\,{}_1F_1\left(\genfrac{}{}{0pt}{}{a}{c}\,;\,z\right).\]

---

Last modified on May 16, 2021