Analyse – Vectoren – Inwendig product

Definitie: Als \(\mathbf{a}=\langle a_1,a_2,a_3 \rangle\) en \(\mathbf{b}=\langle b_1,b_2,b_3 \rangle\), dan is het inwendig product van \(\mathbf{a}\) en \(\mathbf{b}\) het getal \(\mathbf{a}\cdot\mathbf{b}\) gegeven door

\[\mathbf{a}\cdot\mathbf{b}=a_1b_1+a_2b_2+a_3b_3.\]

Dit inwendig product heeft de volgende eigenschappen:

Stelling: Als \(\mathbf{a}\), \(\mathbf{b}\) en \(\mathbf{c}\) vectoren in \(\mathbb{R}^3\) zijn, dan geldt:

1. \(\mathbf{a}\cdot\mathbf{b}=\mathbf{b}\cdot\mathbf{a}\)


2. \(\mathbf{a}\cdot(\mathbf{b}+\mathbf{c})=\mathbf{a}\cdot\mathbf{b}+\mathbf{a}\cdot\mathbf{c}\)


3. \((\lambda\mathbf{a})\cdot\mathbf{b}=\lambda(\mathbf{a}\cdot\mathbf{b})=\mathbf{a}\cdot(\lambda\mathbf{b})\) voor elke \(\lambda\in\mathbb{R}\)


4. \(\mathbf{a}\cdot\mathbf{a}=|\mathbf{a}|^2\)

Stelling: Als \(\theta\) de hoek is tussen \(\mathbf{a}\) en \(\mathbf{b}\), dan is

\[\mathbf{a}\cdot\mathbf{b}=|\mathbf{a}||\mathbf{b}|\cos(\theta),\quad 0\leq\theta\leq\pi.\]

Definitie: Twee vectoren \(\mathbf{a}\) en \(\mathbf{b}\) zijn orthogonaal dan en slechts dan als \(\mathbf{a}\cdot\mathbf{b}=0\). Notatie: \(\mathbf{a}\perp\mathbf{b}\).

Definitie: De (orthogonale) projectie van \(\mathbf{b}\) op \(\mathbf{a}\neq\mathbf{0}\) is

\[\text{proj}_{\mathbf{a}}\mathbf{b}=\left(\frac{\mathbf{b}\cdot\mathbf{a}}{\mathbf{a}\cdot\mathbf{a}}\right)\mathbf{a}.\]

Toepassing:

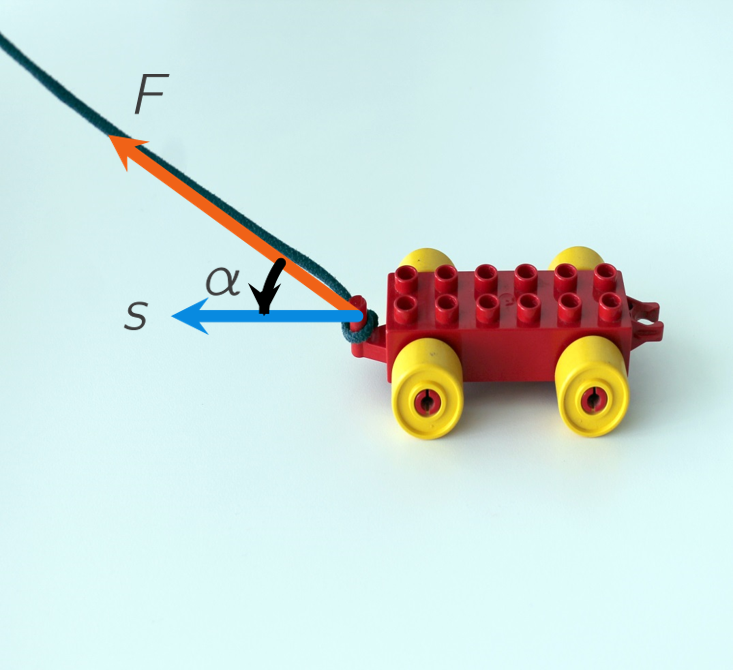
De arbeid \(W\) verricht door een kracht \(\mathbf{F}\):


Als \(\mathbf{s}\) de verplaatsing aangeeft en \(\alpha\) is de hoek tussen \(\mathbf{F}\) en \(\mathbf{s}\), dan is


\(W=|\mathbf{F}||\mathbf{s}|\cos(\alpha)\).


Hieruit volgt dat \(W=\mathbf{F}\cdot\mathbf{s}\).

Voorbeeld:

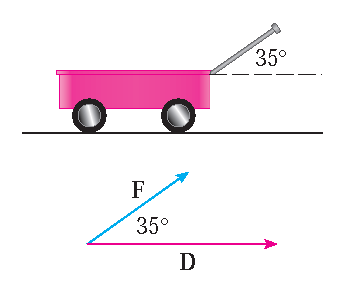
Stewart §12.3, Voorbeeld 7
Een wagentje wordt over een afstand van \(100\) m voortgetrokken over een horizontale weg door een constante kracht van \(70\) N. Het handvat van het wagentje wordt in een hoek van \(35^{\circ}\) boven horizontaal gehouden. Bepaal de arbeid verricht door de kracht.

Oplossing:
Als \(\mathbf{F}\) en \(\mathbf{D}\) de kracht- en verplaatsingsvectoren zijn , zoals aangegeven in het plaatje links, dan is de verrichte arbeid \(W\) gelijk aan

\(W=\mathbf{F}\cdot\mathbf{D}=|\mathbf{F}||\mathbf{D}|\cos(35^{\circ})=70\cdot100\cdot\cos(35^{\circ})\approx5734\,\text{N}\,\text{m}=5734\,\text{J}\).

Het vinden van hoeken:

Stewart §12.3, Opgave 55
Bepaal de hoek tussen een diagonaal van een kubus en één van de ribben.

Oplossing:
Laten we aannemen dat de kubus wordt opgespannen door de vectoren \(\mathbf{i}=\langle 1,0,0 \rangle\), \(\mathbf{j}=\langle 0,1,0 \rangle\) en \(\mathbf{k}=\langle 0,0,1 \rangle\). Dan willen we de hoek tussen \(\mathbf{a}=\mathbf{i}+\mathbf{j}+\mathbf{k}=\langle 1,1,1 \rangle\) en \(\mathbf{b}=\mathbf{i}=\langle 1,0,0, \rangle\) (bijvoorbeeld) bepalen. Nu geldt dat

\[\mathbf{a}\cdot\mathbf{b}=1,\quad|\mathbf{a}|=\sqrt{3}\quad\text{en}\quad|\mathbf{b}|=1.\]

Als we de hoek \(\theta\) noemen, dan volgt hieruit dat:

\[\cos(\theta)=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{a}||\mathbf{b}|}=\frac{1}{\sqrt{3}}.\]

Merk op dat er slechts één waarde van \(\theta\in(0,\pi)\) is waarvoor \(\cos(\theta)=\frac{1}{\sqrt{3}}\).

Gebruikmakend van de knop \(\cos^{-1}\) op uw rekenmachine vinden we dat \(\theta\approx55^{\circ}\). Zie inverse trigonometrische functies voor meer informatie over deze functie.

Stewart §12.3, Opgave 56
Bepaal de hoek tussen een diagonaal van een kubus en een diagonaal van één van de zijden.

Oplossing:
In dit geval willen we de hoek tussen \(\mathbf{a}=\mathbf{i}+\mathbf{j}+\mathbf{k}=\langle 1,1,1 \rangle\) en \(\mathbf{b}=\mathbf{i}+\mathbf{j}=\langle 1,1,0, \rangle\) (bijvoorbeeld) bepalen. Dan geldt dat

\[\mathbf{a}\cdot\mathbf{b}=2,\quad|\mathbf{a}|=\sqrt{3}\quad\text{en}\quad|\mathbf{b}|=\sqrt{2}.\]

Als we de hoek \(\theta\) noemen, dan volgt hieruit dat:

\[\cos(\theta)=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{a}||\mathbf{b}|}=\frac{2}{\sqrt{3}\sqrt{2}}=\frac{2}{\sqrt{6}}.\]

Merk op dat er slechts één waarde van \(\theta\in(0,\pi)\) is waarvoor \(\cos(\theta)=\frac{2}{\sqrt{6}}\).

Gebruikmakend van de knop \(\cos^{-1}\) op uw rekenmachine vinden we dat \(\theta\approx35^{\circ}\). Zie inverse trigonometrische functies voor meer informatie over deze functie.

Stewart §12.3, Opgave 57
Een molecuul methaan, \(CH_4\), wordt gevormd door vier waterstofatomen op de hoeken van een regelmatig viervlak en het koolstofatoom in het zwaartepunt. De bindingshoek is de hoek gevormd door de \(H−C−H\) combinatie; dit is de hoek tussen de lijnen die het koolstofatoom verbinden met twee van de waterstofatomen. Toon aan dat de bindingshoek ongeveer gelijk is aan \(109.5^{\circ}\).

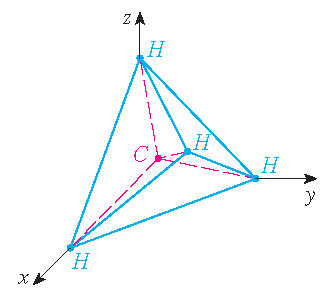
Oplossing:
Als we voor de hoekpunten van het viervlak de punten \((1,0,0)\), \((0,1,0)\), \((0,0,1)\) en \((1,1,1)\) kiezen, zoals getoond in het plaatje, dan is het zwaartepunt \((\frac{1}{2},\frac{1}{2},\frac{1}{2})\). Nu willen de hoek θ bepalen tussen de vectoren

\[\mathbf{a}=\langle \frac{1}{2},-\frac{1}{2},-\frac{1}{2} \rangle\quad\text{en}\quad\mathbf{b}=\langle -\frac{1}{2},-\frac{1}{2},\frac{1}{2} \rangle\quad\text{(bijvoorbeeld)}.\]

Dan geldt:

\[\cos(\theta)=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{a}||\mathbf{b}|}=\frac{-\frac{1}{4}+\frac{1}{4}-\frac{1}{4}}{\frac{1}{2}\sqrt{3}\cdot\frac{1}{2}\sqrt{3}}=-\frac{1}{3}.\]

Merk op dat er slechts één waarde van \(\theta\in(0,\pi)\) is waarvoor \(\cos(\theta)=-\frac{1}{3}\).

Gebruikmakend van de knop \(\cos^{-1}\) op uw rekenmachine vinden we dat \(\theta\approx109.5^{\circ}\). Zie inverse trigonometrische functies voor meer informatie over deze functie.

Merk op dat als \(\cos(\theta)>0\) dan is de hoek \(\theta\) scherp (\(0<\theta<\frac{1}{2}\pi\)) en als \(\cos(\theta)<0\) dan is de hoek \(\theta\) stomp (\(\frac{1}{2}\pi<\theta<\pi\)).

Toepassing: de parallellogramwet (Stewart §12.3, Opgave 63)

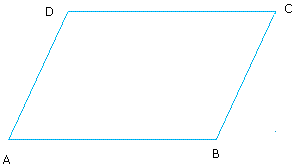	De parallellogramwet zegt dat \(|AC|^2+|BD|^2=2|AB|^2+2|AD|^2\).
Als we de oorsprong in het punt \(A\) kiezen, dan is: \(AD=\mathbf{u},\quad AB=\mathbf{v},\) \(AC=\mathbf{u}+\mathbf{v}\) en \(|BD|=|\mathbf{u}-\mathbf{v}|\)

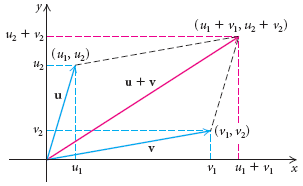Dus, in termen van vectoren luidt de parallellogramwet:

\[|\mathbf{u}+\mathbf{v}|^2+|\mathbf{u}-\mathbf{v}|^2=2|\mathbf{u}|^2+2|\mathbf{v}|^2.\]

Gebruikmakend van de eigenschappen van het inwendig product,is het bewijs eenvoudig:

\begin{align*}|\mathbf{u}+\mathbf{v}|^2+|\mathbf{u}-\mathbf{v}|^2&=(\mathbf{u}+\mathbf{v})\cdot(\mathbf{u}+\mathbf{v})+(\mathbf{u}-\mathbf{v})\cdot(\mathbf{u}-\mathbf{v})\\[2.5mm] &=\mathbf{u}\cdot\mathbf{u}+\mathbf{u}\cdot\mathbf{v}+\mathbf{v}\cdot\mathbf{u}+\mathbf{v}\cdot\mathbf{v} +\mathbf{u}\cdot\mathbf{u}-\mathbf{u}\cdot\mathbf{v}-\mathbf{v}\cdot\mathbf{u}+\mathbf{v}\cdot\mathbf{v}\\[2.5mm] &=2(\mathbf{u}\cdot\mathbf{u})+2(\mathbf{v}\cdot\mathbf{v})=2|\mathbf{u}|^2+2|\mathbf{v}|^2.\end{align*}

---

Laatst gewijzigd op 1 maart 2021