Calculus – Vectors – Dot product
Definition: If \(\mathbf{a}=\langle a_1,a_2,a_3 \rangle\) and \(\mathbf{b}=\langle b_1,b_2,b_3 \rangle\), then the dot product of \(\mathbf{a}\) and \(\mathbf{b}\) is the number \(\mathbf{a}\cdot\mathbf{b}\) given by
\[\mathbf{a}\cdot\mathbf{b}=a_1b_1+a_2b_2+a_3b_3.\]This dot product satisfies the following properties:
Theorem: If \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\) are vectors in \(\mathbb{R}^3\), then we have:
- \(\mathbf{a}\cdot\mathbf{b}=\mathbf{b}\cdot\mathbf{a}\)
- \(\mathbf{a}\cdot(\mathbf{b}+\mathbf{c})=\mathbf{a}\cdot\mathbf{b}+\mathbf{a}\cdot\mathbf{c}\)
- \((\lambda\mathbf{a})\cdot\mathbf{b}=\lambda(\mathbf{a}\cdot\mathbf{b})=\mathbf{a}\cdot(\lambda\mathbf{b})\) for each \(\lambda\in\mathbb{R}\)
- \(\mathbf{a}\cdot\mathbf{a}=|\mathbf{a}|^2\)
Theorem: If \(\theta\) is the angle between \(\mathbf{a}\) and \(\mathbf{b}\), then
\[\mathbf{a}\cdot\mathbf{b}=|\mathbf{a}||\mathbf{b}|\cos(\theta),\quad 0\leq\theta\leq\pi.\]Definition: Two vectors \(\mathbf{a}\) and \(\mathbf{b}\) are orthogonal if and only if \(\mathbf{a}\cdot\mathbf{b}=0\). Notation: \(\mathbf{a}\perp\mathbf{b}\).
Definition: The (orthogonal) projection of \(\mathbf{b}\) onto \(\mathbf{a}\neq\mathbf{0}\) is
\[\text{proj}_{\mathbf{a}}\mathbf{b}=\left(\frac{\mathbf{b}\cdot\mathbf{a}}{\mathbf{a}\cdot\mathbf{a}}\right)\mathbf{a}.\]Application:
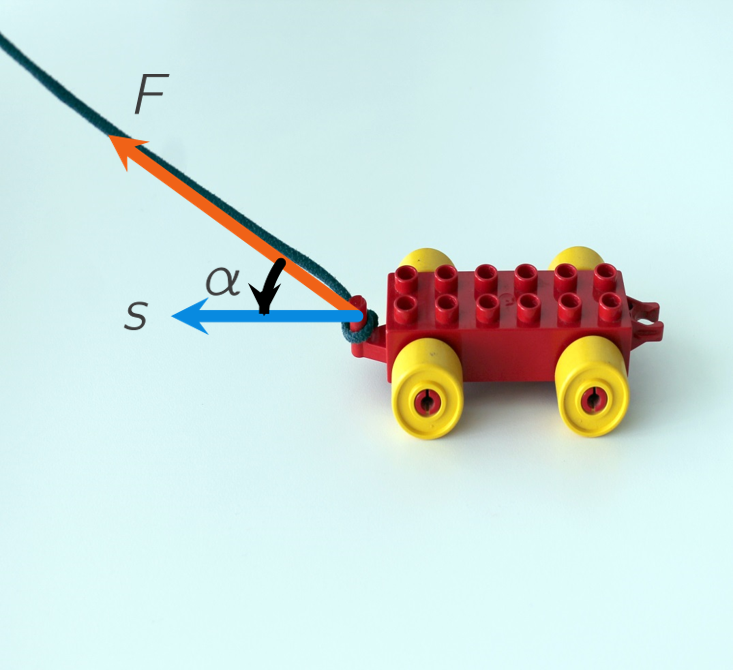
The work \(W\) done by a force \(\mathbf{F}\):
If \(\mathbf{s}\) is the displacement and \(\alpha\) the angle between \(\mathbf{F}\) and \(\mathbf{s}\), then:
\(W=|\mathbf{F}||\mathbf{s}|\cos(\alpha)\).
This implies that \(W=\mathbf{F}\cdot\mathbf{s}\).
Example:
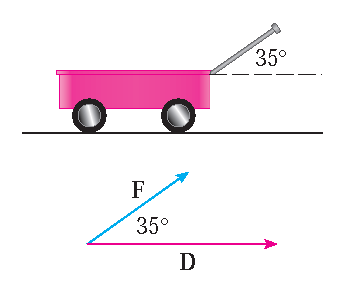
Stewart §12.3, Example 7
A wagon is pulled a distance of \(100\) m along a horizontal path by a constant force of \(70\) N. The handle of the wagon is held at an angle of
\(35^{\circ}\) above the horizontal. Find the work done by the force.
Solution:
If \(\mathbf{F}\) and \(\mathbf{D}\) are the force and displacement vectors, as pictured at the left,
then the work \(W\) done equals
\(W=\mathbf{F}\cdot\mathbf{D}=|\mathbf{F}||\mathbf{D}|\cos(35^{\circ})=70\cdot100\cdot\cos(35^{\circ})\approx5734\,\text{N}\,\text{m}=5734\,\text{J}\).
Finding angles:
Stewart §12.3, Exercise 55
Find the angle between a diagonal of a cube and one of its edges.
Solution:
Let's assume that the cube is spanned by the vectors \(\mathbf{i}=\langle 1,0,0 \rangle\), \(\mathbf{j}=\langle 0,1,0 \rangle\) and
\(\mathbf{k}=\langle 0,0,1 \rangle\). Then we want to find the angle between \(\mathbf{a}=\mathbf{i}+\mathbf{j}+\mathbf{k}=\langle 1,1,1 \rangle\)
and \(\mathbf{b}=\mathbf{i}=\langle 1,0,0, \rangle\) (for instance). Now we have
If we call the angle \(\theta\), this implies that:
\[\cos(\theta)=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{a}||\mathbf{b}|}=\frac{1}{\sqrt{3}}.\]Note that there is only one value of \(\theta\in(0,\pi)\) such that \(\cos(\theta)=\frac{1}{\sqrt{3}}\).
Using the button \(\cos^{-1}\) on your calculator we find that \(\theta\approx55^{\circ}\). See inverse trigonometric functions for more information about this function.
Stewart §12.3, Exercise 56
Find the angle between a diagonal of a cube and a diagonal of one of its faces.
Solution:
In this case we want to find the angle between \(\mathbf{a}=\mathbf{i}+\mathbf{j}+\mathbf{k}=\langle 1,1,1 \rangle\)
and \(\mathbf{b}=\mathbf{i}+\mathbf{j}=\langle 1,1,0, \rangle\) (for instance). Then we have
If we call the angle \(\theta\), this implies that:
\[\cos(\theta)=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{a}||\mathbf{b}|}=\frac{2}{\sqrt{3}\sqrt{2}}=\frac{2}{\sqrt{6}}.\]Note that there is only one value of \(\theta\in(0,\pi)\) such that \(\cos(\theta)=\frac{2}{\sqrt{6}}\).
Using the button \(\cos^{-1}\) on your calculator we find that \(\theta\approx35^{\circ}\). See inverse trigonometric functions for more information about this function.
Stewart §12.3, Exercise 57
A molecule of methane, \(CH_4\), is structured with the four hydrogen atoms at the vertices of a regular tetrahedron and the carbon atom at the
centroid. The bond angle is the angle formed by the \(H−C−H\) combination; it is the angle between the lines that join the carbon atom to two of
the hydrogen atoms. Show that the bond angle is about \(109.5^{\circ}\).
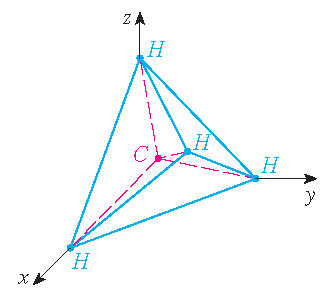
Solution:
If we take the vertices of the tetrahedron to be the points \((1,0,0)\), \((0,1,0)\), \((0,0,1)\) and \((1,1,1)\), as shown in the picture,
then the centroid is \((\frac{1}{2},\frac{1}{2},\frac{1}{2})\). Now we want to find the angle θ between the vectors
Then we have:
\[\cos(\theta)=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{a}||\mathbf{b}|}=\frac{-\frac{1}{4}+\frac{1}{4}-\frac{1}{4}}{\frac{1}{2}\sqrt{3}\cdot\frac{1}{2}\sqrt{3}}=-\frac{1}{3}.\]Note that there is only one value of \(\theta\in(0,\pi)\) such that \(\cos(\theta)=-\frac{1}{3}\).
Using the button \(\cos^{-1}\) on your calculator we find that \(\theta\approx109.5^{\circ}\). See inverse trigonometric functions for more information about this function.
Note that if \(\cos(\theta)>0\) then the angle \(\theta\) is acute (\(0<\theta<\frac{1}{2}\pi\)) and if \(\cos(\theta)<0\) then the angle \(\theta\) is obtuse (\(\frac{1}{2}\pi<\theta<\pi\)).
Application: the parallelogram law (Stewart §12.3, Exercise 63)
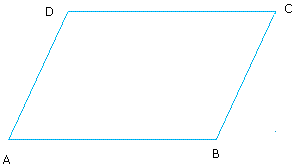 |
The parallelogram law states that \(|AC|^2+|BD|^2=2|AB|^2+2|AD|^2\). |
If we put the origin in the point \(A\), then: \(AD=\mathbf{u},\quad AB=\mathbf{v},\) \(AC=\mathbf{u}+\mathbf{v}\) and \(|BD|=|\mathbf{u}-\mathbf{v}|\) |
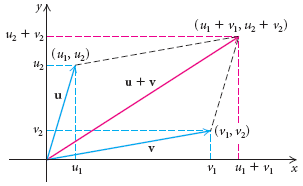 |
So, in terms of vectors the parallelogram law reads:
\[|\mathbf{u}+\mathbf{v}|^2+|\mathbf{u}-\mathbf{v}|^2=2|\mathbf{u}|^2+2|\mathbf{v}|^2.\]Using the properties of the dot product, the proof is easy:
\begin{align*}|\mathbf{u}+\mathbf{v}|^2+|\mathbf{u}-\mathbf{v}|^2&=(\mathbf{u}+\mathbf{v})\cdot(\mathbf{u}+\mathbf{v})+(\mathbf{u}-\mathbf{v})\cdot(\mathbf{u}-\mathbf{v})\\[2.5mm] &=\mathbf{u}\cdot\mathbf{u}+\mathbf{u}\cdot\mathbf{v}+\mathbf{v}\cdot\mathbf{u}+\mathbf{v}\cdot\mathbf{v} +\mathbf{u}\cdot\mathbf{u}-\mathbf{u}\cdot\mathbf{v}-\mathbf{v}\cdot\mathbf{u}+\mathbf{v}\cdot\mathbf{v}\\[2.5mm] &=2(\mathbf{u}\cdot\mathbf{u})+2(\mathbf{v}\cdot\mathbf{v})=2|\mathbf{u}|^2+2|\mathbf{v}|^2.\end{align*}Another proof of Thales's theorem
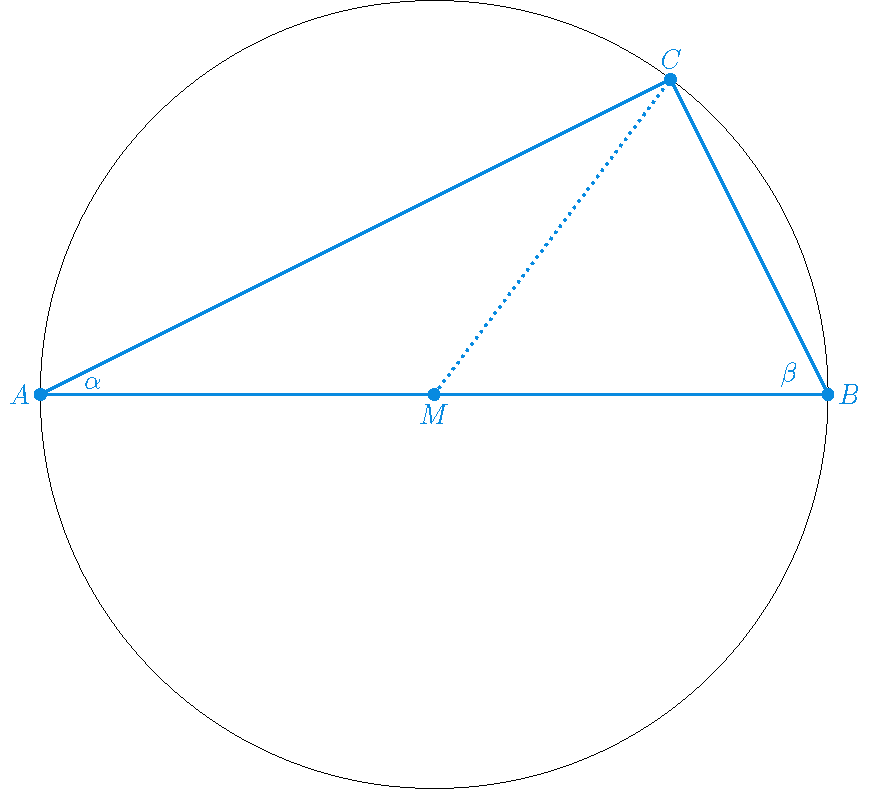
If \(AB\) is a diameter of a circle and \(C\) is an arbitrary point on the circle, not equal to \(A\) or \(B\), then the angle \(ACB\) equals \(90^{\circ}\).
Proof: Let the center \(M\) of the circle be the origin. Then we have: \(A=(-r,0)\) and \(B=(r,0)\), where \(r\) denotes the radius of the circle (without loss of generality). Now \(C=(x,y)\) is an arbitrary point on the circle, so: \(x^2+y^2=r^2\).
Now we have: \(\overrightarrow{AC}=\langle x+r,y\rangle\) and \(\overrightarrow{BC}=\langle x-r,y\rangle\). Hence:
\[\overrightarrow{AC}\cdot\overrightarrow{BC}=(x+r)(x-r)+y^2=x^2+y^2-r^2=0\quad\Longrightarrow\quad\angle ACB=90^{\circ}.\]Last modified on March 1, 2021
 Teaching
Teaching

