Calculus – Vectors – Cross product

Definition: The cross product of \(\mathbf{a}=\langle a_1,a_2,a_3 \rangle\) and \(\mathbf{b}=\langle b_1,b_2,b_3 \rangle\) is

\[\mathbf{a}\times\mathbf{b}=\langle a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1 \rangle.\]

Definition: The determinant of a \(2\times2\) matrix is: \(\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad-bc\).

Then we have: \(\mathbf{a}\times\mathbf{b}=\begin{vmatrix}a_2&a_3\\b_2&b_3\end{vmatrix}\,\mathbf{i}-\begin{vmatrix}a_1&a_3\\b_1&b_3\end{vmatrix}\,\mathbf{j}+\begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix}\,\mathbf{k}\).

The cross product satisfies the following properties:

Theorem: If \(\mathbf{v}=\mathbf{a}\times\mathbf{b}\) and \(\theta\) is the angle between \(\mathbf{a}\) and \(\mathbf{b}\), then

1. \(\mathbf{v}\perp\mathbf{a}\) and \(\mathbf{v}\perp\mathbf{b}\),


2. \(|\mathbf{v}|=|\mathbf{a}||\mathbf{b}|\sin(\theta)\),


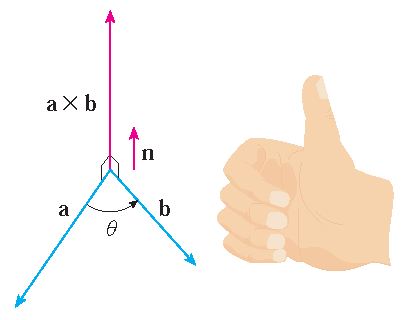
3. \(\{\mathbf{a},\mathbf{b},\mathbf{v}\}\) is positively oriented.

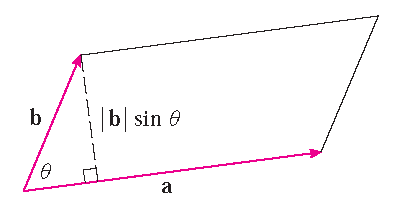\(\{\mathbf{a},\mathbf{b},\mathbf{v}\}\) satisfies the right-hand rule	\(|\mathbf{a}\times\mathbf{b}|=|\mathbf{a}||\mathbf{b}|\sin(\theta)\) is the area of the parallelogram spanned by \(\mathbf{a}\) and \(\mathbf{b}\)

For the cross product we have the following rules of calculation:

Theorem: If \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\) are vectors in \(\mathbb{R}^3\), then we have:

1. \(\mathbf{b}\times\mathbf{a}=-(\mathbf{a}\times\mathbf{b})\),


2. \((\lambda\mathbf{a})\times\mathbf{b}=\lambda(\mathbf{a}\times\mathbf{b})=\mathbf{a}\times(\lambda\mathbf{b})\) for each \(\lambda\in\mathbb{R}\)


3. \(\mathbf{a}\times(\mathbf{b}+\mathbf{c})=(\mathbf{a}\times\mathbf{b})+(\mathbf{a}\times\mathbf{c})\)


4. \(\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})=(\mathbf{a}\times\mathbf{b})\cdot\mathbf{c}\)


5. \(\mathbf{a}\times(\mathbf{b}\times\mathbf{c})=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c}\)

The product in 4. is called a scalar triple product and the product in 5. is called a vector triple product.

Definition: If \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\) are vectors in \(\mathbb{R}^3\), then the scalar triple product of \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\) is \(\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})\).

Geometric interpretation:

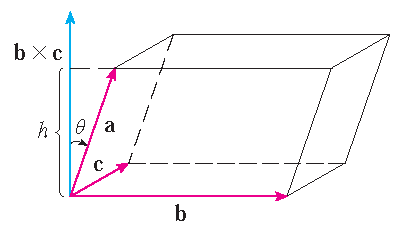
\(|\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})|\) equals the volume
of the parallelepiped spanned by
the vectors \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\).

Definition: The determinant of a \(3\times3\) matrix is: \(\begin{vmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix} =a_1\begin{vmatrix}b_2&b_3\\c_2&c_3\end{vmatrix}-a_2\begin{vmatrix}b_1&b_3\\c_1&c_3\end{vmatrix}+a_3\begin{vmatrix}b_1&b_2\\c_2&c_2\end{vmatrix}\).

Theorem: If \(\mathbf{a}=\langle a_1,a_2,a_3 \rangle\), \(\mathbf{b}=\langle b_1,b_2,b_3 \rangle\) and \(\mathbf{c}=\langle c_1,c_2,c_3 \rangle\), then: \(\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})=\begin{vmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix}\).

Application:

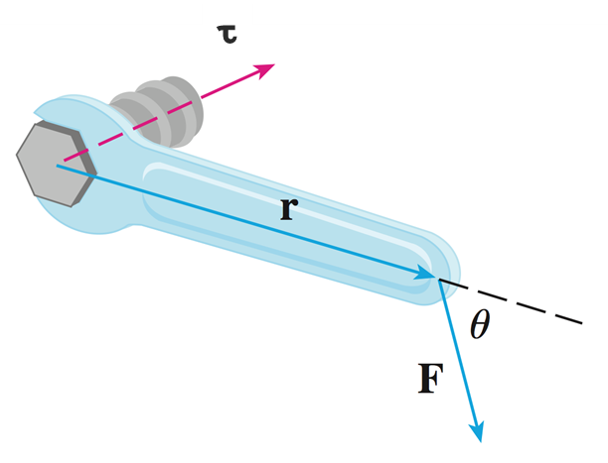
The torque \(\boldsymbol{\tau}\) by a force \(\mathbf{F}\):


\(\boldsymbol{\tau}=\mathbf{r}\times\mathbf{F}\).


\(|\boldsymbol{\tau}|=|\mathbf{r}||\mathbf{F}|\sin(\theta)\).

Example:

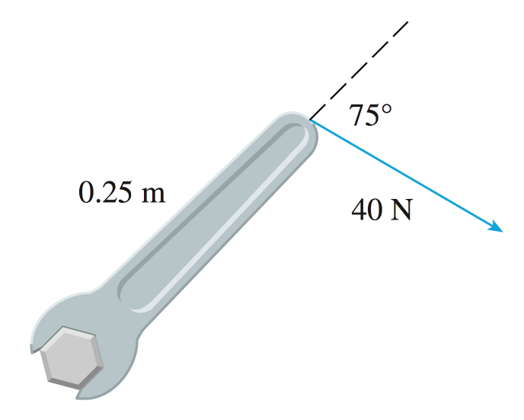
Stewart §12.4, Example 6
A bolt is tightened by applying a force of \(40\) N to a wrench of \(25\) cm as shown in the picture. Find the magnitude of the torque about the center of the bolt.

Solution:
\(|\boldsymbol{\tau}|=|\mathbf{r}||\mathbf{F}|\sin(\theta)=0.25\cdot40\cdot\sin(75^{\circ})=10\sin(75^{\circ})\approx9.66\,\text{N}\,\text{m}\).

The area of a triangle

Consider a triangle \(ABC\) with vertices \(A\), \(B\) and \(C\).

If we denote the position vectors of these vertices by \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\) respectively and we put the origin at the point \(A\), then we have:

\[\overrightarrow{AB}=\mathbf{b}-\mathbf{a}\quad\text{and}\quad\overrightarrow{AC}=\mathbf{c}-\mathbf{a}.\]

Since the area of the triangle is half the area of the parallelogram spanned by these vectors, we have:

\[\text{area}(ABC)=\frac{1}{2}|(\mathbf{b}-\mathbf{a})\times(\mathbf{c}-\mathbf{a})|.\]

Examples:

If \(A=(3,-1,2)\), \(B=(1,2,-3)\) and \(C=(-2,3,-7)\), then

\[\mathbf{b}-\mathbf{a}=\langle -2,3,-5 \rangle\quad\text{and}\quad\mathbf{c}-\mathbf{a}=\langle -5,4,-9 \rangle\]

and the area of the triangle \(ABC\) equals

\[\text{area}(ABC)=\frac{1}{2}|(\mathbf{b}-\mathbf{a})\times(\mathbf{c}-\mathbf{a})|=\frac{1}{2}|\langle -7,7,7 \rangle| =\frac{7}{2}\langle -1,1,1 \rangle=\frac{7}{2}\sqrt{3}.\]

If \(A=(-2,3,-1)\), \(B=(3,-2,4)\) and \(C=(1,1,2)\), then

\[\mathbf{b}-\mathbf{a}=\langle 5,-5,5 \rangle\quad\text{and}\quad\mathbf{c}-\mathbf{a}=\langle 3,-2,3 \rangle\]

and the area of the triangle \(ABC\) equals

\[\text{area}(ABC)=\frac{1}{2}|(\mathbf{b}-\mathbf{a})\times(\mathbf{c}-\mathbf{a})|=\frac{1}{2}|\langle -5,0,5 \rangle| =\frac{5}{2}\langle -1,0,1 \rangle=\frac{5}{2}\sqrt{2}.\]

It also works for points in \(\mathbb{R}^2\): if \(A=(-6,3)\), \(B=(1,-2)\) and \(C=(3,4)\), then

\[\mathbf{b}-\mathbf{a}=\langle 7,-5,0 \rangle\quad\text{and}\quad\mathbf{c}-\mathbf{a}=\langle 9,1,0 \rangle\]

and the area of the triangle \(ABC\) equals

\[\text{area}(ABC)=\frac{1}{2}|(\mathbf{b}-\mathbf{a})\times(\mathbf{c}-\mathbf{a})|=\frac{1}{2}|\langle 0,0,52 \rangle|=26.\]

Proof of the vector triple product formula (Stewart §12.4, Exercise 50)
If \(\mathbf{a}=\langle a_1,a_2,a_3 \rangle\), \(\mathbf{b}=\langle b_1,b_2,b_3 \rangle\) and \(\mathbf{c}=\langle c_1,c_2,c_3 \rangle\) are vectors in \(\mathbb{R}^3\), then

\[\mathbf{a}\times(\mathbf{b}\times\mathbf{c})=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c}.\]

Proof:
Start with \[\mathbf{b}\times\mathbf{c}=\langle b_2c_3-b_3c_2,b_3c_1-b_1c_3,b_1c_2-b_2c_1 \rangle.\]

Then we have:

\begin{align*}\mathbf{a}\times(\mathbf{b}\times\mathbf{c})&=\langle a_2(b_1c_2-b_2c_1)-a_3(b_3c_1-b_1c_3),a_3(b_2c_3-b_3c_2)-a_1(b_1c_2-b_2c_1),a_1(b_3c_1-b_1c_3,)-a_2(b_2c_3-b_3c_2) \rangle\\[2.5mm] &=\langle (a_2c_2+a_3c_3)b_1-(a_2b_2+a_3b_3)c_1,(a_1c_1+a_3c_3)b_2-(a_1b_1+a_3b_3)c_2,(a_1c_1+a_2c_2)b_3-(a_1b_1+a_2b_2)c_3 \rangle\\[2.5mm] &=\langle (a_1c_1+a_2c_2+a_3c_3)b_1-(a_1b_1+a_2b_2+a_3b_3)c_1,\\[2.5mm] &{}\hspace{25mm}{}(a_1c_1+a_2c_2+a_3c_3)b_2-(a_1b_1+a_2b_2+a_3b_3)c_2,\\[2.5mm] &{}\hspace{50mm}(a_1c_1+a_2c_2+a_3c_3)b_3-(a_1b_1+a_2b_2+a_3b_3)c_3 \rangle\\[2.5mm] &=(a_1c_1+a_2c_2+a_3c_3)\mathbf{b}-(a_1b_1+a_2b_2+a_3b_3)\mathbf{c}=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c}. \end{align*}

The formula is sometimes called the \(BAC-CAB\) formula and written as

\[\mathbf{a}\times(\mathbf{b}\times\mathbf{c})=\mathbf{b}(\mathbf{a}\cdot\mathbf{c})-\mathbf{c}(\mathbf{a}\cdot\mathbf{b}).\]

In this form it is easier to remember.

---

Last modified on March 1, 2021