Analyse – Vectoren – Uitwendig product

Definitie: Het uitwendig product van \(\mathbf{a}=\langle a_1,a_2,a_3 \rangle\) en \(\mathbf{b}=\langle b_1,b_2,b_3 \rangle\) is

\[\mathbf{a}\times\mathbf{b}=\langle a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1 \rangle.\]

Definitie: De determinant van een \(2\times2\) matrix is: \(\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad-bc\).

Dan geldt: \(\mathbf{a}\times\mathbf{b}=\begin{vmatrix}a_2&a_3\\b_2&b_3\end{vmatrix}\,\mathbf{i}-\begin{vmatrix}a_1&a_3\\b_1&b_3\end{vmatrix}\,\mathbf{j}+\begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix}\,\mathbf{k}\).

Het uitwendig product heeft de volgende eigenschappen:

Stelling: Als \(\mathbf{v}=\mathbf{a}\times\mathbf{b}\) en \(\theta\) is de hoek tussen \(\mathbf{a}\) en \(\mathbf{b}\), dan

1. \(\mathbf{v}\perp\mathbf{a}\) en \(\mathbf{v}\perp\mathbf{b}\),


2. \(|\mathbf{v}|=|\mathbf{a}||\mathbf{b}|\sin(\theta)\),


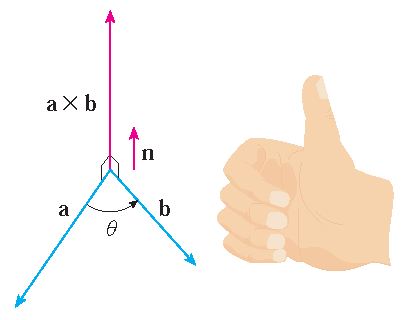
3. \(\{\mathbf{a},\mathbf{b},\mathbf{v}\}\) is positief geörienteerd.

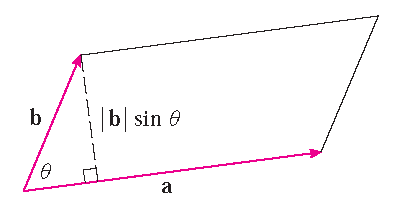\(\{\mathbf{a},\mathbf{b},\mathbf{v}\}\) voldoet aan de rechterhandregel	\(|\mathbf{a}\times\mathbf{b}|=|\mathbf{a}||\mathbf{b}|\sin(\theta)\) is de oppervlakte van het parallellogram opgespannen door \(\mathbf{a}\) en \(\mathbf{b}\)

Voor het uitwendig product gelden de volgende rekenregels:

Theorem: Als \(\mathbf{a}\), \(\mathbf{b}\) en \(\mathbf{c}\) vectoren in \(\mathbb{R}^3\) zijn, dan geldt:

1. \(\mathbf{b}\times\mathbf{a}=-(\mathbf{a}\times\mathbf{b})\),


2. \((\lambda\mathbf{a})\times\mathbf{b}=\lambda(\mathbf{a}\times\mathbf{b})=\mathbf{a}\times(\lambda\mathbf{b})\) voor elke \(\lambda\in\mathbb{R}\)


3. \(\mathbf{a}\times(\mathbf{b}+\mathbf{c})=(\mathbf{a}\times\mathbf{b})+(\mathbf{a}\times\mathbf{c})\)


4. \(\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})=(\mathbf{a}\times\mathbf{b})\cdot\mathbf{c}\)


5. \(\mathbf{a}\times(\mathbf{b}\times\mathbf{c})=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c}\)

Het product in 4. heet een scalair tripelproduct en het product in 5. heet een vector tripelproduct.

Definitie: Als \(\mathbf{a}\), \(\mathbf{b}\) en \(\mathbf{c}\) vectoren in \(\mathbb{R}^3\) zijn, dan is het scalartripelproduct van \(\mathbf{a}\), \(\mathbf{b}\) en \(\mathbf{c}\) gelijk aan \(\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})\).

Meetkundige interpretatie:

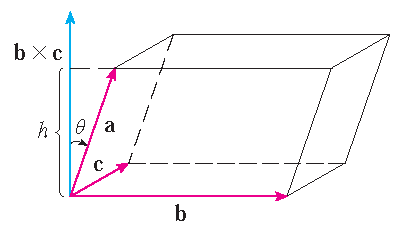
\(|\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})|\) is gelijk aan de inhoud
van het parallellepipedum opgespannen door
de vectoren \(\mathbf{a}\), \(\mathbf{b}\) en \(\mathbf{c}\).

Definitie: De determinant van een \(3\times3\) matrix is: \(\begin{vmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix} =a_1\begin{vmatrix}b_2&b_3\\c_2&c_3\end{vmatrix}-a_2\begin{vmatrix}b_1&b_3\\c_1&c_3\end{vmatrix}+a_3\begin{vmatrix}b_1&b_2\\c_2&c_2\end{vmatrix}\).

Stelling: Als \(\mathbf{a}=\langle a_1,a_2,a_3 \rangle\), \(\mathbf{b}=\langle b_1,b_2,b_3 \rangle\) en \(\mathbf{c}=\langle c_1,c_2,c_3 \rangle\), dan: \(\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})=\begin{vmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix}\).

Toepassing:

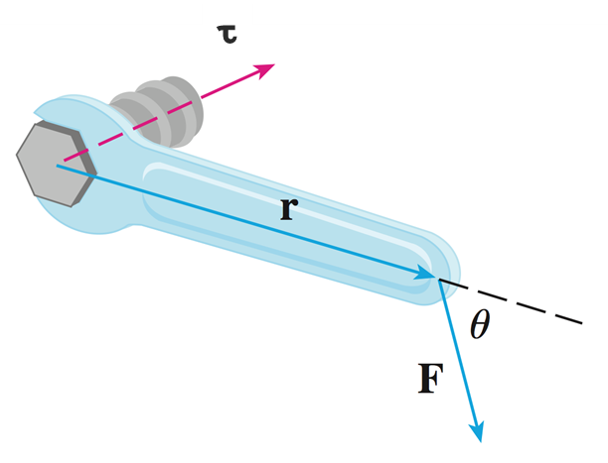
Het koppel \(\boldsymbol{\tau}\) van een kracht \(\mathbf{F}\):


\(\boldsymbol{\tau}=\mathbf{r}\times\mathbf{F}\).


\(|\boldsymbol{\tau}|=|\mathbf{r}||\mathbf{F}|\sin(\theta)\).

Voorbeeld:

Stewart §12.4, Voorbeeld 6
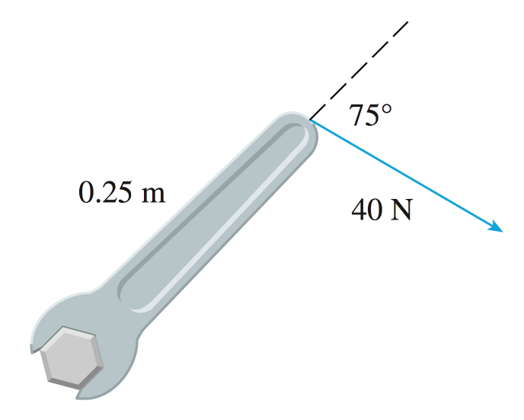
Een bout wordt aangedraaid door toepassing van een kracht van \(40\) N op een steeksleutel van \(25\) cm zoals aangegeven in het plaatje. Bepaal de grootte van het koppel ten opzichte van het centrum van de bout.

Oplossing:
\(|\boldsymbol{\tau}|=|\mathbf{r}||\mathbf{F}|\sin(\theta)=0.25\cdot40\cdot\sin(75^{\circ})=10\sin(75^{\circ})\approx9.66\,\text{N}\,\text{m}\).

De oppervlakte van een driehoek

Beschouw een driehoek \(ABC\) met hoekpunten \(A\), \(B\) en \(C\).

Als we de positievectoren van deze hoekpunten aanduiden met \(\mathbf{a}\), \(\mathbf{b}\) en \(\mathbf{c}\) respectievelijk en we kiezen de oorsprong in het punt \(A\), dan geldt:

\[\overrightarrow{AB}=\mathbf{b}-\mathbf{a}\quad\text{en}\quad\overrightarrow{AC}=\mathbf{c}-\mathbf{a}.\]

Omdat de oppervlakte van de driehoek de helft is van de oppervlakte van het parallellogram opgespannen door deze vectoren, geldt dat:

\[\text{opp}(ABC)=\frac{1}{2}|(\mathbf{b}-\mathbf{a})\times(\mathbf{c}-\mathbf{a})|.\]

Voorbeelden:

Als \(A=(3,-1,2)\), \(B=(1,2,-3)\) en \(C=(-2,3,-7)\), dan is

\[\mathbf{b}-\mathbf{a}=\langle -2,3,-5 \rangle\quad\text{en}\quad\mathbf{c}-\mathbf{a}=\langle -5,4,-9 \rangle\]

en is de oppervlakte van de driehoek \(ABC\) gelijk aan

\[\text{opp}(ABC)=\frac{1}{2}|(\mathbf{b}-\mathbf{a})\times(\mathbf{c}-\mathbf{a})|=\frac{1}{2}|\langle -7,7,7 \rangle| =\frac{7}{2}\langle -1,1,1 \rangle=\frac{7}{2}\sqrt{3}.\]

Als \(A=(-2,3,-1)\), \(B=(3,-2,4)\) en \(C=(1,1,2)\), dan is

\[\mathbf{b}-\mathbf{a}=\langle 5,-5,5 \rangle\quad\text{en}\quad\mathbf{c}-\mathbf{a}=\langle 3,-2,3 \rangle\]

en is de oppervlakte van de driehoek \(ABC\) gelijk aan

\[\text{opp}(ABC)=\frac{1}{2}|(\mathbf{b}-\mathbf{a})\times(\mathbf{c}-\mathbf{a})|=\frac{1}{2}|\langle -5,0,5 \rangle| =\frac{5}{2}\langle -1,0,1 \rangle=\frac{5}{2}\sqrt{2}.\]

Het werkt ook met punten in \(\mathbb{R}^2\): als \(A=(-6,3)\), \(B=(1,-2)\) en \(C=(3,4)\), dan is

\[\mathbf{b}-\mathbf{a}=\langle 7,-5,0 \rangle\quad\text{en}\quad\mathbf{c}-\mathbf{a}=\langle 9,1,0 \rangle\]

en is de oppervlakte van de driehoek \(ABC\) gelijk aan

\[\text{opp}(ABC)=\frac{1}{2}|(\mathbf{b}-\mathbf{a})\times(\mathbf{c}-\mathbf{a})|=\frac{1}{2}|\langle 0,0,52 \rangle|=26.\]

Bewijs van de vector tripelproduct formule (Stewart §12.4, Opgave 50)
Als \(\mathbf{a}=\langle a_1,a_2,a_3 \rangle\), \(\mathbf{b}=\langle b_1,b_2,b_3 \rangle\) en \(\mathbf{c}=\langle c_1,c_2,c_3 \rangle\) vectoren in \(\mathbb{R}^3\) zijn, dan

\[\mathbf{a}\times(\mathbf{b}\times\mathbf{c})=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c}.\]

Bewijs:
Begin met \[\mathbf{b}\times\mathbf{c}=\langle b_2c_3-b_3c_2,b_3c_1-b_1c_3,b_1c_2-b_2c_1 \rangle.\]

Dan geldt:

\begin{align*}\mathbf{a}\times(\mathbf{b}\times\mathbf{c})&=\langle a_2(b_1c_2-b_2c_1)-a_3(b_3c_1-b_1c_3),a_3(b_2c_3-b_3c_2)-a_1(b_1c_2-b_2c_1),a_1(b_3c_1-b_1c_3,)-a_2(b_2c_3-b_3c_2) \rangle\\[2.5mm] &=\langle (a_2c_2+a_3c_3)b_1-(a_2b_2+a_3b_3)c_1,(a_1c_1+a_3c_3)b_2-(a_1b_1+a_3b_3)c_2,(a_1c_1+a_2c_2)b_3-(a_1b_1+a_2b_2)c_3 \rangle\\[2.5mm] &=\langle (a_1c_1+a_2c_2+a_3c_3)b_1-(a_1b_1+a_2b_2+a_3b_3)c_1,\\[2.5mm] &{}\hspace{25mm}{}(a_1c_1+a_2c_2+a_3c_3)b_2-(a_1b_1+a_2b_2+a_3b_3)c_2,\\[2.5mm] &{}\hspace{50mm}(a_1c_1+a_2c_2+a_3c_3)b_3-(a_1b_1+a_2b_2+a_3b_3)c_3 \rangle\\[2.5mm] &=(a_1c_1+a_2c_2+a_3c_3)\mathbf{b}-(a_1b_1+a_2b_2+a_3b_3)\mathbf{c}=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c}. \end{align*}

De formule wordt soms de \(BAC-CAB\) formule genoemd en geschreven als

\[\mathbf{a}\times(\mathbf{b}\times\mathbf{c})=\mathbf{b}(\mathbf{a}\cdot\mathbf{c})-\mathbf{c}(\mathbf{a}\cdot\mathbf{b}).\]

In deze vorm is het makkelijker te onthouden.

---

Laatst gewijzigd op 1 maart 2021