OnderwijsAnalyse – Tweede orde differentiaalvergelijkingen – Toepassingen
De slinger
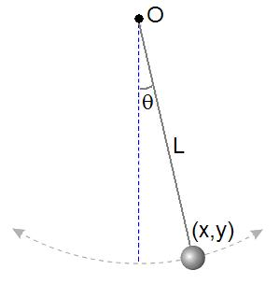De
differentiaalvergelijking die de beweging van een enkelvoudige slinger weergeeft is :
\(\displaystyle\frac{d^2\theta}{dt^2}+\frac{g}{L}\sin(\theta)=0\),
waarbij \(g\) de zwaartekrachtversnelling is, \(L\) de lengte van de slinger en \(\theta\) de
hoekverplaatsing ten opzichte van de evenwichtsstand op tijdstip \(t\).
Het is behoorlijk lastig om deze differentiaalvergelijking op te lossen.
Echter, de linearisering van de functie \(f(x)=\sin(x)\) rond \(x=0\) is
\[L(x)=f(0)+f'(0)(x-0)=x.\]Hieruit volgt dat \(\sin(\theta)\approx\theta\) voor \(\theta\) in de buurt van \(0\).
Merk op dat het veel eenvoudiger is om in plaats die hierboven de differentiaalvergelijking
\[\frac{d^2\theta}{dt^2}+\frac{g}{L}\theta=0\]op te lossen. Dit is een homgene tweede orde lineaire differentiaalvergelijking met constante coëfficiënten. De karakteristieke vergelijking is
\[r^2+\frac{g}{L}=0\quad\Longrightarrow\quad r=\pm i\sqrt{\frac{g}{l}}.\]Hieruit volgt dat de algemene oplossing gelijk is aan
\[\theta(t)=c_1\cos(rt)+c_2\sin(rt)\quad\text{met}\quad r=\sqrt{\frac{g}{L}}\quad\text{en}\quad c_1,c_2\in\mathbb{R}.\]Dus, als (bijvoorbeeld) de beginpositie van de slinger \(\theta_0\) is en deze wordt losgelaten zonder beginsnelheid, dan leidt dit tot het beginwaardeprobleem
\[\theta''(t)+\frac{g}{L}\theta(t)=0,\quad\theta(0)=\theta_0,\quad\theta'(0)=0\]met oplossing \(\theta(t)=\theta_0\cos(\sqrt{\frac{g}{L}}t)\).
Een massa-veer systeem
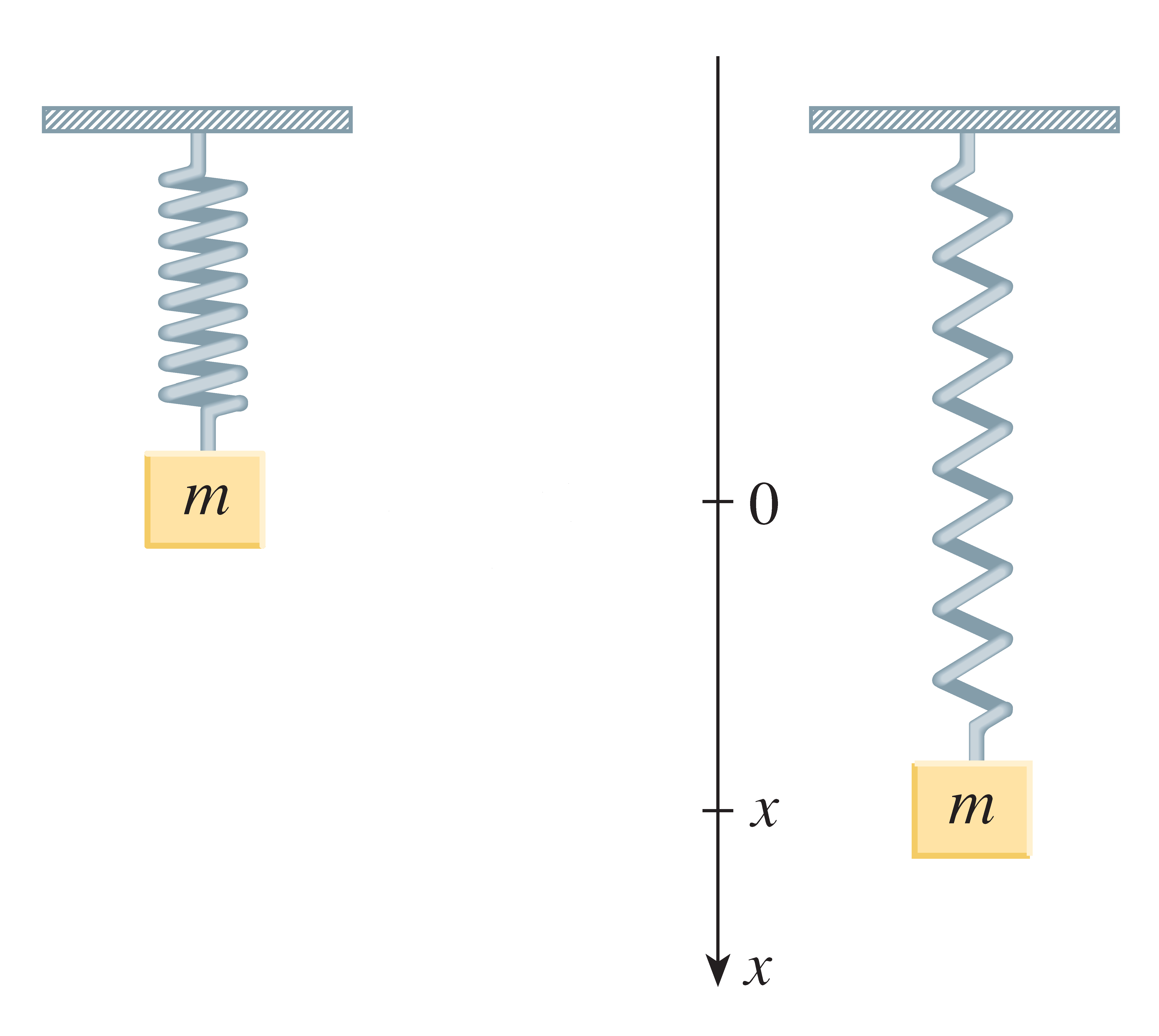Stewart §17.3
Wet van Newton: \(F=m\cdot a\).
Wet van Hooke: \(F=-k\cdot x\).
Hieruit volgt:
\(m\cdot\displaystyle\frac{d^2x}{dt^2}=-k\cdot x(t)\),
waarbij \(k\) een positieve constante is, die de veerconstante wordt genoemd.
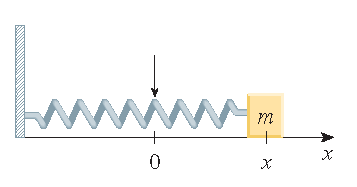
Zonder demping:
\(mx''(t)+kx(t)=0\).
Met demping: \(mx''(t)+cx'(t)+kx(t)=0\),
hier is \(c\) een positieve constante, die de dempingsconstante wordt genoemd.
Stewart §17.3, Voorbeeld 1
Een veer met een massa van \(2\;\text{kg}\) heeft een natuurlijke lengte van \(0.5\;\text{m}\). Een kracht van \(25.6\;\text{N}\) is benodigd
om deze uitgerekt te houden tot een lengte van \(0.7\;\text{m}\). Als de veer wordt uitgerekt tot een lengte van \(0.7\;\text{m}\) en dan
wordt losgelaten met beginsnelheid \(0\), bepaal dan de positie van de massa op tijdstip \(t\).
Oplossing:
Uit de wet van Hooke volgt dat de kracht die nodig is om de veer uit te rekken gelijk is aan \(k\cdot(0.2)=25.6\), dus \(k=\displaystyle\frac{25.6}{0.2}=128\).
Gebruikmakend van deze waarde van de veerconstante \(k\), samen met \(m=2\) volgt dat
De algemene oplossing is \(x(t)=c_1\cos(8t)+c_2\sin(8t)\) waaruit volgt dat \(x'(t)=-8c_1\sin(8t)+8c_2\cos(8t)\). De beginvoorwaarden zijn \(x(0)=0.2\) en \(x'(0)=0\), die leiden tot \(c_1=0.2\) en \(c_2=0\). Dus, de oplossing is \(x(t)=0.2\cos(8t)\).
Stewart §17.3, Voorbeeld 2
Neem aan dat de veer wordt ondergedompeld in een vloeistof met dempingsconstante \(c=40\). Bepaal de positie van de massa op tijstip \(t\) als
deze wordt gestart in de evenwichtspositie met een beginsnelheid van \(0.6\;\text{m}/\text{s}\).
Oplossing:
Met \(m=2\) en \(k=128\) wordt de differentiaalvergelijking
De karakteristieke vergelijking is \(r^2+20r+64=0\;\Longleftrightarrow\;(r+4)(r+16)=0\) met wortels \(r=-4\) en \(r=-16\). Dus, de algemene oplossing is \(x(t)=c_1e^{-4t}+c_2e^{-16t}\) waaruit volgt dat \(x'(t)=-4c_1e^{-4t}-16c_2e^{-16t}\). De beginvoorwaarden zijn \(x(0)=0\) en \(x'(0)=0.6\), die leiden tot \(c_1=0.05\) en \(c_2=-0.05\). Dus, de oplossing is \(x(t)=0.05\left(e^{-4t}-e^{-16t}\right)\).
Nog een voorbeeld van de methode van Feynman (zie: de methode van Feynman)
Beschouw de integraal \(I(t)=\displaystyle\int_0^{\infty}\frac{\cos(xt)}{x^2+\alpha^2}\,dx\) met \(\alpha>0\). Dan volgt: \(I(0)=\displaystyle\int_0^{\infty}\frac{dx}{x^2+\alpha^2}=\frac{1}{\alpha}\arctan\left(\frac{x}{\alpha}\right)\bigg|_0^{\infty}=\frac{\pi}{2\alpha}\) en
\[I'(t)=-\int_0^{\infty}\frac{x\sin(xt)}{x^2+\alpha^2}\,dx=-\int_0^{\infty}\frac{(x^2+\alpha^2-\alpha^2)\sin(xt)}{x(x^2+\alpha^2)}\,dx =-\int_0^{\infty}\frac{\sin(xt)}{x}\,dx+\alpha^2\int_0^{\infty}\frac{\sin(xt)}{x(x^2+\alpha^2)}\,dx.\]Met behulp van de substitutie \(xt=u\) volgt voor \(t>0\) dat \(\displaystyle\int_0^{\infty}\frac{\sin(xt)}{x}\,dx=\int_0^{\infty}\frac{\sin(u)}{u}\,du=\frac{1}{2}\pi\) (zie: de Dirichlet integraal). Dus:
\[I'(t)=-\frac{1}{2}\pi+\alpha^2\int_0^{\infty}\frac{\sin(xt)}{x(x^2+\alpha^2)}\,dx.\]Nu volgt: \(I'(0)=-\dfrac{1}{2}\pi\) en \(I''(t)=\alpha^2\displaystyle\int_0^{\infty}\frac{\cos(xt)}{x^2+\alpha^2}\,dx=\alpha^2I(t)\).
Dus: \(I(t)=c_1e^{\alpha t}+c_2e^{-\alpha t}\) en \(I'(t)=\alpha c_1e^{\alpha t}-\alpha c_2e^{-\alpha t}\) met \(I(0)=\dfrac{\pi}{2\alpha}\) en \(I'(0)=-\dfrac{1}{2}\pi\).
Hieruit volgt: \(c_1+c_2=\dfrac{\pi}{2\alpha}\) en \(c_1-c_2=-\dfrac{\pi}{2\alpha}\). Dus: \(c_1=0\) en \(c_2=\dfrac{\pi}{2\alpha}\).
Conclusie: \(I(t)=\dfrac{\pi}{2\alpha}e^{-\alpha t}\) voor \(\alpha>0\) en \(t>0\).
Laatst gewijzigd op 20 april 2024
