Calculus – Second-order differential equations – Applications

The pendulum

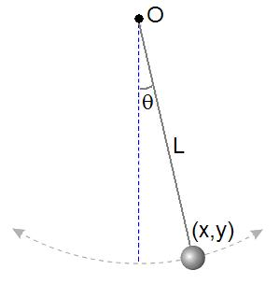The differential equation which represents the motion of a simple pendulum is :

\(\displaystyle\frac{d^2\theta}{dt^2}+\frac{g}{L}\sin(\theta)=0\),

where \(g\) is acceleration due to gravity, \(L\) is the length of the pendulum, and \(\theta\) is
the angular displacement with respect to the equilibrium position at time \(t\).

It is quite difficult to solve this differential equation.

However, the linearization of the function \(f(x)=\sin(x)\) at \(x=0\) is

\[L(x)=f(0)+f'(0)(x-0)=x.\]

This implies that \(\sin(\theta)\approx\theta\) for \(\theta\) near \(0\).

Note that it is much easier to solve the differential equation

\[\frac{d^2\theta}{dt^2}+\frac{g}{L}\theta=0\]

instead of the one above. In fact, this is a homogeneous second-order linear differential equation with constant coefficients. The auxiliary or characteristic equation is

\[r^2+\frac{g}{L}=0\quad\Longrightarrow\quad r=\pm i\sqrt{\frac{g}{l}}.\]

This implies that the general solution is

\[\theta(t)=c_1\cos(rt)+c_2\sin(rt)\quad\text{with}\quad r=\sqrt{\frac{g}{L}}\quad\text{and}\quad c_1,c_2\in\mathbb{R}.\]

So, if (for instance) the starting position of the pundulum is \(\theta_0\) and is released with no initial velocity, then this leads to the initial-value problem

\[\theta''(t)+\frac{g}{L}\theta(t)=0,\quad\theta(0)=\theta_0,\quad\theta'(0)=0\]

with solution \(\theta(t)=\theta_0\cos(\sqrt{\frac{g}{L}}t)\).

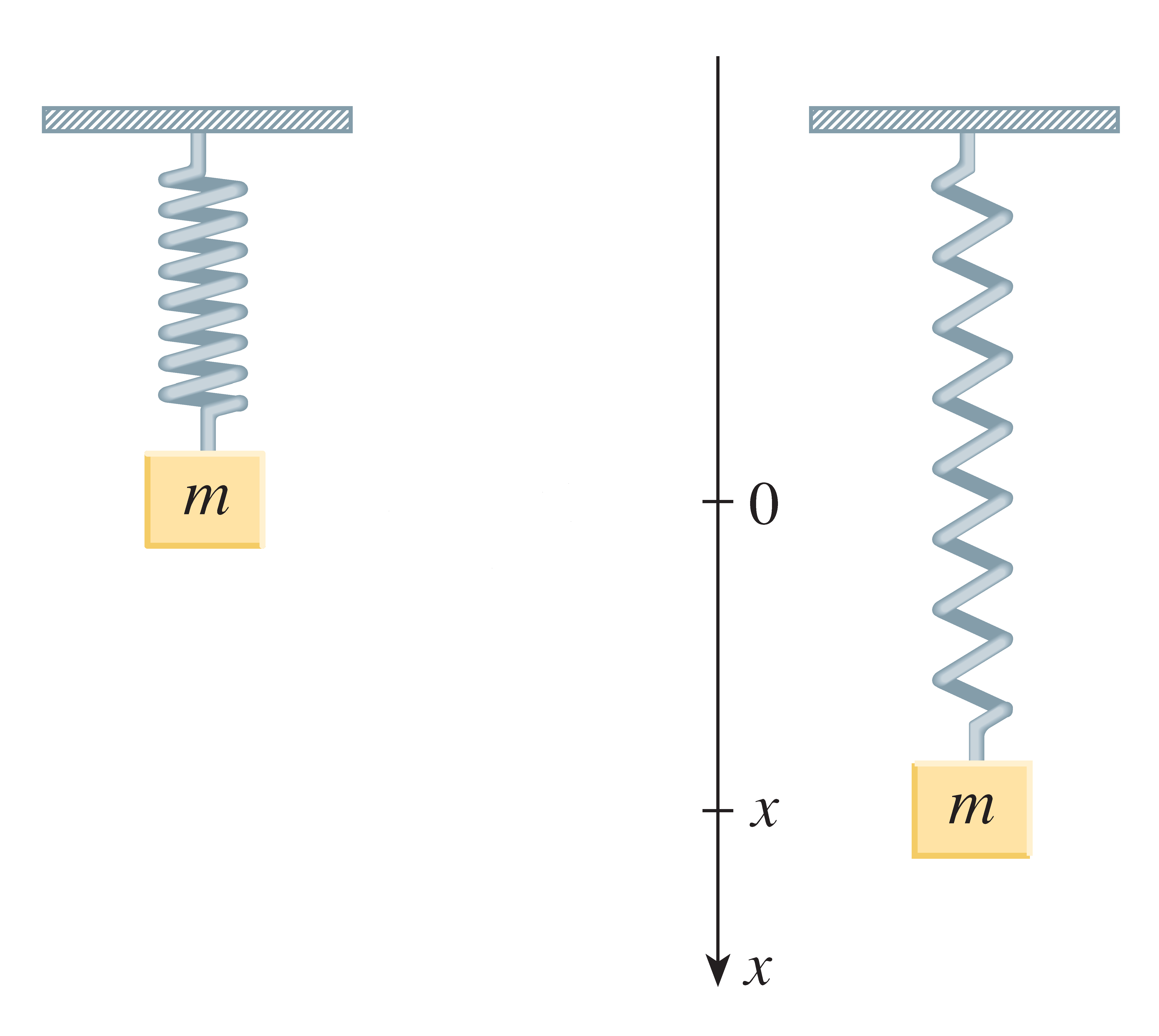
A mass-spring system

Stewart §17.3

Newton's law: \(F=m\cdot a\).

Hooke's law: \(F=-k\cdot x\).

This implies:

\(m\cdot\displaystyle\frac{d^2x}{dt^2}=-k\cdot x(t)\),

where \(k\) is a positive constant, called the spring constant.

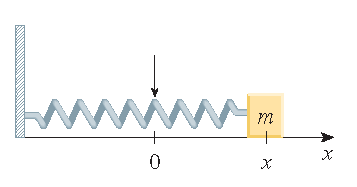
Without damping:

\(mx''(t)+kx(t)=0\).

With damping: \(mx''(t)+cx'(t)+kx(t)=0\),

here \(c\) is a positive constant, called the damping constant.

Stewart §17.3, Example 1
A spring with a mass of \(2\;\text{kg}\) has natural length \(0.5\;\text{m}\). A force of \(25.6\;\text{N}\) is required to maintain it stretched to a length of \(0.7\;\text{m}\). If the spring is stretched to a length of \(0.7\;\text{m}\) and then released with initial velocity \(0\), find the position of the mass at any time \(t\).

Solution:
From Hooke's law, the force required to stretch the spring is \(k\cdot(0.2)=25.6\), so \(k=\displaystyle\frac{25.6}{0.2}=128\). Using this value of the spring constant \(k\), together with \(m=2\) we have

\[2\frac{d^2x}{dt^2}+128x(t)=0.\]

The general solution is \(x(t)=c_1\cos(8t)+c_2\sin(8t)\) which implies that \(x'(t)=-8c_1\sin(8t)+8c_2\cos(8t)\). The initial conditions are \(x(0)=0.2\) and \(x'(0)=0\), which lead to \(c_1=0.2\) and \(c_2=0\). So, the solution is \(x(t)=0.2\cos(8t)\).

Stewart §17.3, Example 2
Suppose that the spring is immersed in a fluid with damping constant \(c=40\). Find the position of the mass at any time \(t\) if it starts from the equilibrium position and is given a push to start it with an initial velocity of \(0.6\;\text{m}/\text{s}\).

Solution:
With \(m=2\) and \(k=128\) the differential equation becomes

\[2\frac{d^2x}{dt^2}+40\frac{dx}{dt}+128x(t)=0\quad\Longleftrightarrow\quad\frac{d^2x}{dt^2}+20\frac{dx}{dt}+64x(t)=0.\]

The auxiliary or characteristic equation is \(r^2+20r+64=0\;\Longleftrightarrow\;(r+4)(r+16)=0\) with roots \(r=-4\) and \(r=-16\). So, the general solution is \(x(t)=c_1e^{-4t}+c_2e^{-16t}\) which implies that \(x'(t)=-4c_1e^{-4t}-16c_2e^{-16t}\). The initial conditions are \(x(0)=0\) and \(x'(0)=0.6\), which lead to \(c_1=0.05\) and \(c_2=-0.05\). So, the solution is \(x(t)=0.05\left(e^{-4t}-e^{-16t}\right)\).

Another example of the Feynman method (see: the Feynman method)

Consider the integral \(I(t)=\displaystyle\int_0^{\infty}\frac{\cos(xt)}{x^2+\alpha^2}\,dx\) with \(\alpha>0\). Then we have: \(I(0)=\displaystyle\int_0^{\infty}\frac{dx}{x^2+\alpha^2}=\frac{1}{\alpha}\arctan\left(\frac{x}{\alpha}\right)\bigg|_0^{\infty}=\frac{\pi}{2\alpha}\) and

\[I'(t)=-\int_0^{\infty}\frac{x\sin(xt)}{x^2+\alpha^2}\,dx=-\int_0^{\infty}\frac{(x^2+\alpha^2-\alpha^2)\sin(xt)}{x(x^2+\alpha^2)}\,dx =-\int_0^{\infty}\frac{\sin(xt)}{x}\,dx+\alpha^2\int_0^{\infty}\frac{\sin(xt)}{x(x^2+\alpha^2)}\,dx.\]

Using the substitution \(xt=u\) we obtain for \(t>0\) that \(\displaystyle\int_0^{\infty}\frac{\sin(xt)}{x}\,dx=\int_0^{\infty}\frac{\sin(u)}{u}\,du=\frac{1}{2}\pi\) (see: the Dirichlet integral). Hence:

\[I'(t)=-\frac{1}{2}\pi+\alpha^2\int_0^{\infty}\frac{\sin(xt)}{x(x^2+\alpha^2)}\,dx.\]

Now we have: \(I'(0)=-\dfrac{1}{2}\pi\) en \(I''(t)=\alpha^2\displaystyle\int_0^{\infty}\frac{\cos(xt)}{x^2+\alpha^2}\,dx=\alpha^2I(t)\).

Hence: \(I(t)=c_1e^{\alpha t}+c_2e^{-\alpha t}\) and \(I'(t)=\alpha c_1e^{\alpha t}-\alpha c_2e^{-\alpha t}\) with \(I(0)=\dfrac{\pi}{2\alpha}\) and \(I'(0)=-\dfrac{1}{2}\pi\).

This implies: \(c_1+c_2=\dfrac{\pi}{2\alpha}\) and \(c_1-c_2=-\dfrac{\pi}{2\alpha}\). Hence: \(c_1=0\) and \(c_2=\dfrac{\pi}{2\alpha}\).

Conclusion: \(I(t)=\dfrac{\pi}{2\alpha}e^{-\alpha t}\) for \(\alpha>0\) and \(t>0\).

---

Last modified on April 20, 2024