Analyse – Complexe getallen – Berekeningen

Als \(z_1=x_1+iy_1\) met \(x_1,y_1\in\mathbb{R}\) en \(z_2=x_2+iy_2\) met \(x_2,y_2\in\mathbb{R}\), dan geldt: \(z_1\pm z_2=x_1\pm x_2+i\left(y_1\pm y_2\right)\). Verder geldt:

\[z_1z_2=(x_1+iy_1)(x_2+iy_2)=x_1x_2+ix_1y_2+ix_2y_1+i^2y_1y_2=x_1x_2-y_1y_2+i(x_1y_2+x_2y_1).\]

Bij delingen maken we gebruik van de eigenschap dat \(z\overline{z}=|z|^2\in\mathbb{R}\). Bijvoorbeeld:

\[\frac{-1+3i}{2-i}=\frac{-1+3i}{2-i}\cdot\frac{2+i}{2+i}=\frac{-2-i+6i+3i^2}{4-i^2}=\frac{-5+5i}{5}=-1+i.\]

Ter controle: \((-1+i)(2-i)=-2+i+2i-i^2=-1+3i\).

Als \(z_1=r_1e^{i\theta_1}=r_1\left(\cos(\theta_1)+i\sin(\theta)\right)\) en \(z_2=r_2e^{i\theta_2}=r_2\left(\cos(\theta_2)+i\sin(\theta_2)\right)\), dan geldt:

\[z_1z_2=r_1r_2e^{i(\theta_1+\theta_2)}=r_1r_2\left(\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)\right)\quad\text{en}\quad \frac{z_1}{z_2}=\frac{r_1}{r_2}e^{i(\theta_1-\theta_2)}=\frac{r_1}{r_2}\left(\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)\right).\]

De deling uiteraard alleen als \(r_2\neq0\).

Hoofdstelling van de algebra: Voor ieder polynoom \(p(x)\) van de graad \(n\in\{1,2,3,\ldots\}\) geldt dat

\[p(x)=c(x-x_1)(x-x_2)\cdots(x-x_n)\quad\text{met}\quad c,x_1,x_2,\ldots,x_n\in\mathbb{C}.\]

Als \(p(x)\) een reëel polynoom is (alle coëfficiënten zijn reëel), dan komen niet-reële nulpunten alleen in complex geconjugeerde paren voor.

In dat geval geldt: als \(\alpha\in\mathbb{C}\), dan is \((z-\alpha)(z-\overline{\alpha})=z^2-(\alpha+\overline{\alpha})z+\alpha\overline{\alpha}=z^2-2\text{Re}(\alpha)z+|\alpha|^2\).

Voorbeelden: \(z^2-5z+6=(z-2)(z-3)\), \(z^3-3z^2+4z-2=(z-1)(z^2-2z+2)=(z-1)\left((z-1)^2+1\right)\), \(z^4-3z^2-4=(z^2-4)(z^2+1)=(z-2)(z+2)(z^2+1)\) en \(z^5-2z^4-z+2=(z-2)(z^4-1)=(z+1)(z-1)(z-2)(z^2+1)\).

Voor kwadratische vergelijkingen van de vorm \(az^2+bz+c=0\) hebben we dan drie mogelijkheden:

1. \(D=b^2-ac>0:\;z=\displaystyle\frac{-b\pm\sqrt{D}}{2a}\).


2. \(D=b^2-4ac=0:\;z=-\displaystyle\frac{b}{2a}\;\text{(tweemaal)}\).


3. \(D=b^2-4ac<0:\;z=\displaystyle\frac{-b\pm i\sqrt{-D}}{2a}\).

Voor machten van complexe getallen gebruiken we de polaire vorm:

Voorbeelden:

Omdat \(1+i=\sqrt{2}\,e^{\frac{1}{4}\pi i}\) en \(\sqrt{3}-i=2\,e^{-\frac{1}{6}\pi i}\), volgt dat:

\[\frac{(1+i)^6}{(\sqrt{3}-i)^2}=\frac{(\sqrt{2}\,e^{\frac{1}{4}\pi i})^6}{(2\,e^{-\frac{1}{6}\pi i})^3} =\frac{2^3}{2^3}\cdot\frac{e^{\frac{3}{2}\pi i}}{e^{-\frac{1}{2}\pi i}}=e^{2\pi i}=e^0=1.\]

Omdat \(1+i\sqrt{3}=2\,e^{\frac{1}{3}\pi i}\) en \(1-i=\sqrt{2}\,e^{-\frac{1}{4}\pi i}\), volgt dat:

\[\frac{(1+i\sqrt{3})^{25}}{(1-i)^{50}}=\frac{(2\,e^{\frac{1}{3}\pi i})^{25}}{(\sqrt{2}\,e^{-\frac{1}{4}\pi i})^{50}} =\frac{2^{25}}{2^{25}}\cdot\frac{e^{\frac{25}{3}\pi i}}{e^{-\frac{25}{2}\pi i}}=e^{\frac{125}{5}\pi i} =e^{\frac{5}{6}\pi i}=-\tfrac{1}{2}\sqrt{3}+\tfrac{1}{2}i.\]

Los op: \(z^5=4-4i\). Neem aan dat \(z=r\,e^{\theta i}\), dan volgt:

\[z^5=4-4i\quad\Longleftrightarrow\quad r^5e^{5\theta i}=4\sqrt{2}\,e^{-\frac{1}{4}\pi i}\quad\Longleftrightarrow\quad r=\sqrt{2}\;\text{en}\;5\theta=-\tfrac{1}{4}\pi+2k\pi,\;k\in\mathbb{Z}.\]

Dus: \(r=\sqrt{2}\) en \(\theta=-\frac{1}{20}\pi+\frac{2}{5}k\pi\) met \(k\in\mathbb{Z}\).

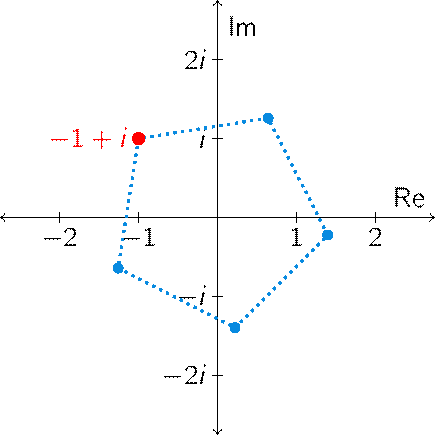Nu vinden we de vijf verschillende oplossingen door
vijf opeenvolgende waarden van \(k\) te kiezen:

1. \(k=0:\;\theta=-\frac{1}{20}\pi\;\Longrightarrow\;z_1=\sqrt{2}e^{-\frac{1}{20}\pi i}\),


2. \(k=1:\;\theta=-\frac{1}{20}\pi+\frac{2}{5}\pi=\frac{7}{20}\pi\;\Longrightarrow\;z_2=\sqrt{2}e^{\frac{7}{20}\pi i}\),


3. \(k=2:\;\theta=-\frac{1}{20}\pi+\frac{4}{5}\pi=\frac{15}{20}\pi=\frac{3}{4}\pi\;\Longrightarrow\;z_3=\sqrt{2}e^{\frac{3}{4}\pi i}=-1+i\),


4. \(k=3:\;\theta=-\frac{1}{20}\pi+\frac{6}{5}\pi=\frac{23}{20}\pi\;\Longrightarrow\;z_4=\sqrt{2}e^{\frac{23}{20}\pi i}=\sqrt{2}e^{-\frac{17}{20}\pi i}\),


5. \(k=4:\;\theta=-\frac{1}{20}\pi+\frac{8}{5}\pi=\frac{31}{20}\pi\;\Longrightarrow\;z_5=\sqrt{2}e^{\frac{31}{20}\pi i}=\sqrt{2}e^{-\frac{9}{20}\pi i}\).

---

Laatst gewijzigd op 1 maart 2021