Analyse – Complexe getallen

Motivatie:

Eerste orde homogene lineaire differentiaalvergelijkingen met constante coëfficiënten hebben oplossingen in de vorm van exponentiële functies.
Bijvoorbeeld: probeer \(y=e^{rx}\) als een oplossing van \(y'+2y=0\), dan vinden we: \(r+2=0\) oftewel \(r=-2\). Dus: \(y=e^{-2x}\) is een oplossing.

Voor tweede orde homogene lineaire differentiaalvergelijkingen met constante coëfficiënten werkt dit principe soms wel, maar soms ook niet.

Bijvoorbeeld: probeer \(y=e^{rx}\) als een oplossing van \(y''+2y'-8y=0\), dan vinden we: \(r^2+2r-8=0\) oftewel \((r+4)(r-2)=0\).
Hieruit volgt dat \(r=-4\) of \(r=2\). Dus: \(y=e^{-4x}\) en \(y=e^{2x}\) zijn oplossingen.

Echter, als we \(y=e^{rx}\) proberen als oplossing van \(y''+2y'+5y=0\), dan vinden we: \(r^2+2r+5=0\) oftewel \((r+1)^2+4=0\).
Dit heeft geen oplossingen voor \(r\in\mathbb{R}\). De differentiaalvergelijking heeft echter wel degelijk oplossingen.

Complexe getallen kunnen worden gebruikt om deze oplossingen te vinden.

Definitie: Het symbool \(i\) is een imaginair getal met de eigenschap dat \(i^2=-1\).

Definitie: Een getal \(z\) van de vorm \(z=x+iy\) met \(x,y\in\mathbb{R}\) heet een complex getal.

\(x=\text{Re}(z)\) heet het reële deel van \(z\).

\(y=\text{Im}(x)\) heet het imaginaire deel van \(z\).

Definitie: Als \(z=x+iy\) met \(x,y\in\mathbb{R}\), dan is \(\overline{z}=x-iy\) de complex geconjugeerde van \(z\).

Complexe getallen kunnen worden weergegeven in het complexe vlak (ook wel: het Argand vlak):

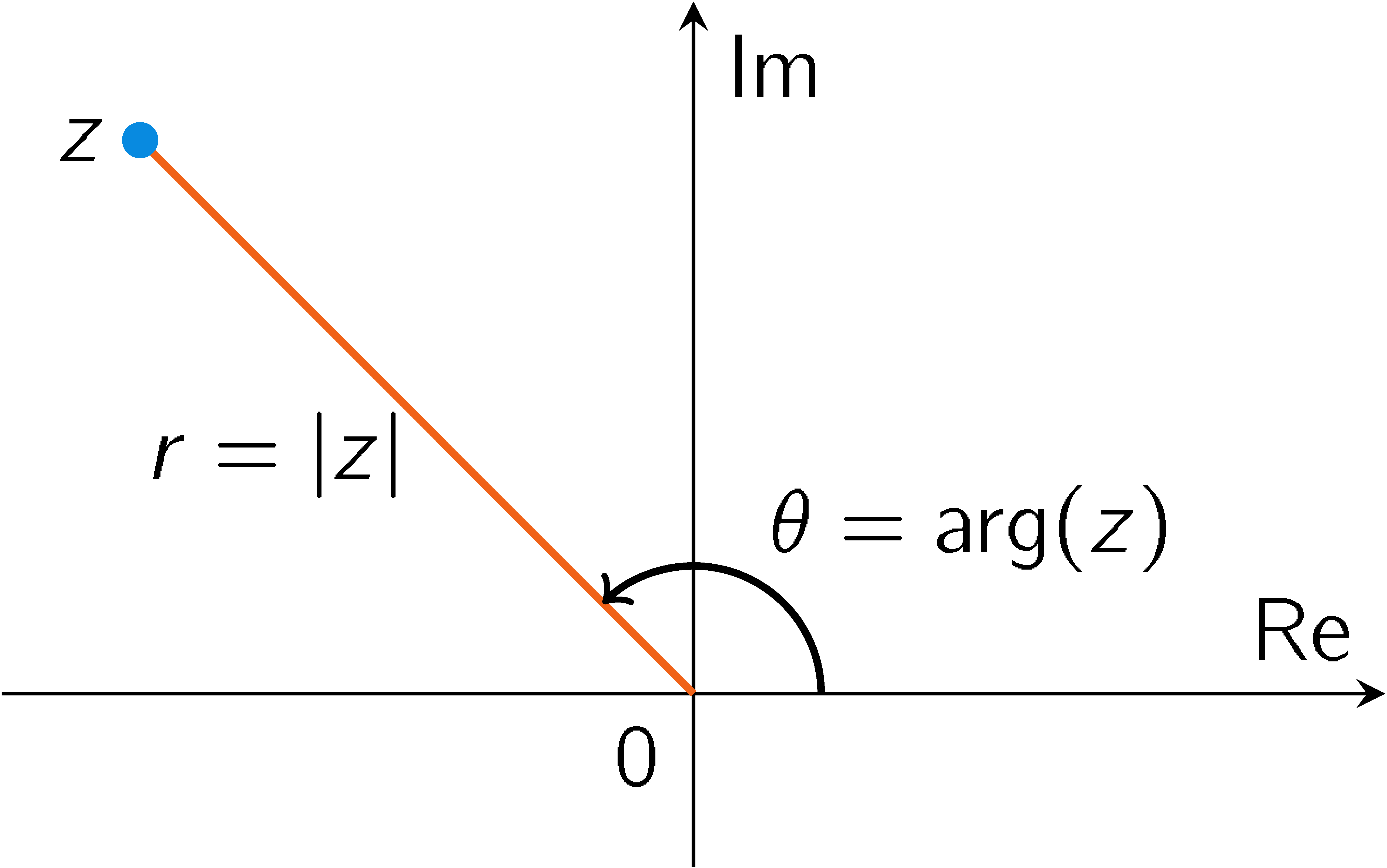
Definitie: Als \(z=x+iy\) met \(x,y\in\mathbb{R}\), dan heet \(r=|z|=\sqrt{x^2+y^2}\), de afstand van \(z\) tot de oorsprong, de modulus van \(z\) en de hoek \(\theta=\arg(z)\) met de positieve reële as heet een argument van \(z\).

De hoek \(\theta=\text{arg}(z)\) is niet uniek; elk tweetal argumenten verschilt een geheel veelvoud van \(2\pi\) van elkaar.

Stelling: Als \(z=x+iy\) met \(x,y\in\mathbb{R}\), dan geldt: \(z\overline{z}=|z|^2\). Verder geldt: \(x=r\cos(\theta)\) en \(y=r\sin(\theta)\).

Definitie: De schrijfwijze \(z=r\left(\cos(\theta)+i\sin(\theta)\right)\) heet een polaire vorm van \(z\).

Formule van Euler: \(e^{\theta i}=\cos(\theta)+i\sin(\theta)\) voor \(\theta\in\mathbb{R}\).

Stelling van De Moivre: Als \(\theta\in\mathbb{R}\), dan is \(\left(\cos(\theta)+i\sin(\theta)\right)^n=\cos(n\theta)+i\sin(n\theta)\) voor \(n\in\mathbb{Z}\).

---

Laatst gewijzigd op 1 maart 2021