Calculus – Complex numbers

Motivation:

First-order homogeneous linear differential equations with constant coefficients have solutions in the form of exponential functions.
For instance: try \(y=e^{rx}\) as a solution of \(y'+2y=0\), then we obtain: \(r+2=0\) or equivalently \(r=-2\). Hence: \(y=e^{-2x}\) is a solution.

For second-order homogeneous linear differential equations with constant coefficients this principle will sometimes work, however sometimes it will not work.

For instance: try \(y=e^{rx}\) as a solution of \(y''+2y'-8y=0\), then we obtain: \(r^2+2r-8=0\) or equivalently \((r+4)(r-2)=0\).
This implies that \(r=-4\) or \(r=2\). Hence: \(y=e^{-4x}\) and \(y=e^{2x}\) are solutions.

However, if we try \(y=e^{rx}\) as a solution of \(y''+2y'+5y=0\), then we obtain: \(r^2+2r+5=0\) or equivalently \((r+1)^2+4=0\).
This has no solutions for \(r\in\mathbb{R}\). However, the differential equation certainly has solutions.

Complex numbers can be used to find these solutions.

Definition: The symbool \(i\) is an imaginary number with the property that \(i^2=-1\).

Definition: A number \(z\) of the form \(z=x+iy\) with \(x,y\in\mathbb{R}\) is called a complex number.

\(x=\text{Re}(z)\) is called the real part of \(z\).

\(y=\text{Im}(x)\) is called the imaginary part of \(z\).

Definition: If \(z=x+iy\) with \(x,y\in\mathbb{R}\), then \(\overline{z}=x-iy\) is the complex geconjugate of \(z\).

Complex numbers can be represented in the complex plane (also called: the Argand plane):

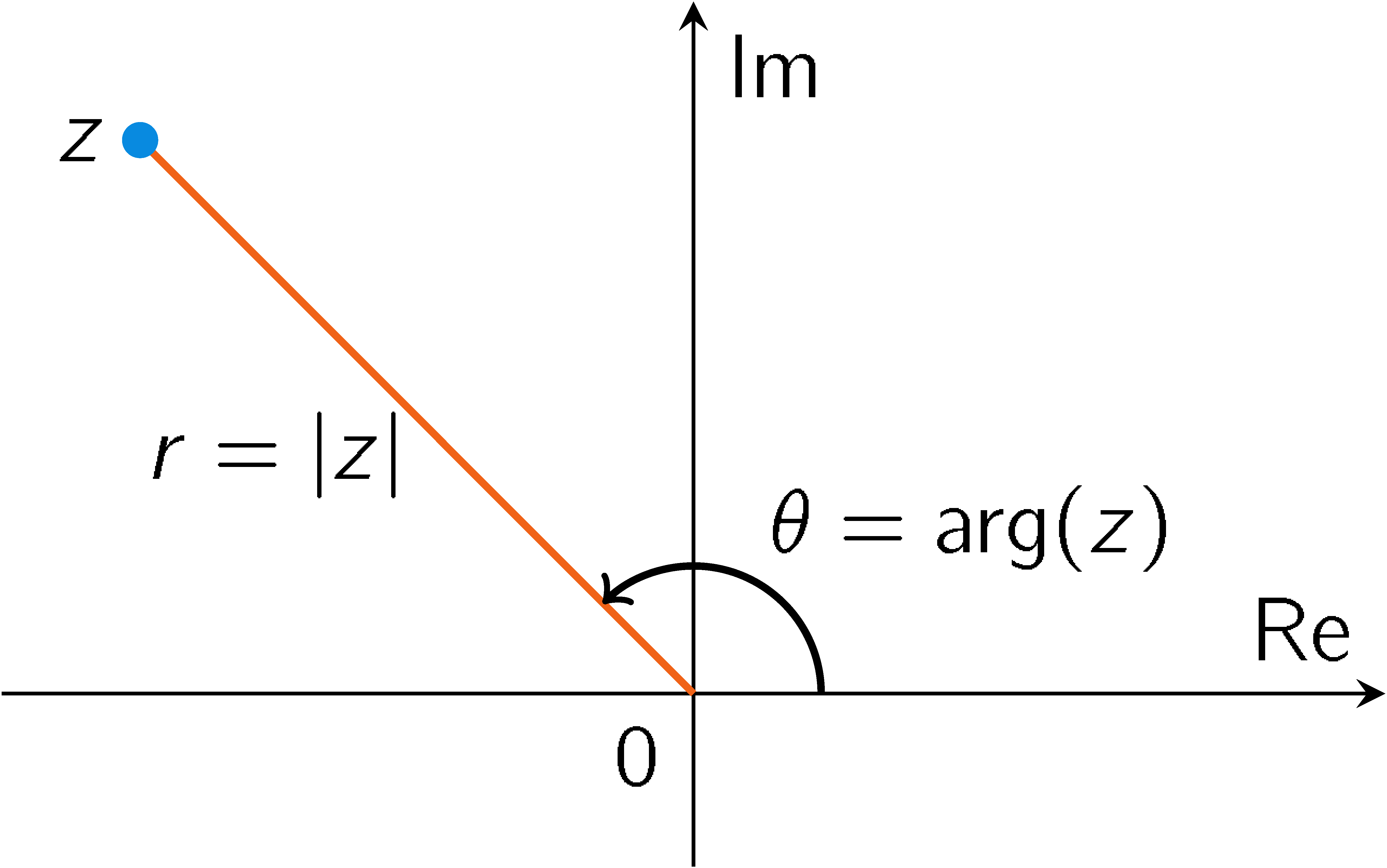
Definition: If \(z=x+iy\) with \(x,y\in\mathbb{R}\), then \(r=|z|=\sqrt{x^2+y^2}\), the distance from \(z\) to the origin, is called the modulus of \(z\) and the angle \(\theta=\arg(z)\) with the positive real axis is called an argument of \(z\).

The angle \(\theta=\text{arg}(z)\) is not unique; any two arguments differ by an integer multiple of \(2\pi\).

Theorem: If \(z=x+iy\) with \(x,y\in\mathbb{R}\), then we have: \(z\overline{z}=|z|^2\). Further we have: \(x=r\cos(\theta)\) and \(y=r\sin(\theta)\).

Definition: The notation \(z=r\left(\cos(\theta)+i\sin(\theta)\right)\) is called a polar form of \(z\).

Euler's formula: \(e^{\theta i}=\cos(\theta)+i\sin(\theta)\) for \(\theta\in\mathbb{R}\).

De Moivre's theorem: If \(\theta\in\mathbb{R}\), then we have \(\left(\cos(\theta)+i\sin(\theta)\right)^n=\cos(n\theta)+i\sin(n\theta)\) for \(n\in\mathbb{Z}\).

---

Last modified on March 1, 2021