Calculus – Complex numbers – Computations

If \(z_1=x_1+iy_1\) with \(x_1,y_1\in\mathbb{R}\) and \(z_2=x_2+iy_2\) with \(x_2,y_2\in\mathbb{R}\), then we have: \(z_1\pm z_2=x_1\pm x_2+i\left(y_1\pm y_2\right)\). Further we have:

\[z_1z_2=(x_1+iy_1)(x_2+iy_2)=x_1x_2+ix_1y_2+ix_2y_1+i^2y_1y_2=x_1x_2-y_1y_2+i(x_1y_2+x_2y_1).\]

For divisions we use the property that \(z\overline{z}=|z|^2\in\mathbb{R}\). For instance:

\[\frac{-1+3i}{2-i}=\frac{-1+3i}{2-i}\cdot\frac{2+i}{2+i}=\frac{-2-i+6i+3i^2}{4-i^2}=\frac{-5+5i}{5}=-1+i.\]

For checking: \((-1+i)(2-i)=-2+i+2i-i^2=-1+3i\).

If \(z_1=r_1e^{i\theta_1}=r_1\left(\cos(\theta_1)+i\sin(\theta)\right)\) and \(z_2=r_2e^{i\theta_2}=r_2\left(\cos(\theta_2)+i\sin(\theta_2)\right)\), then we have:

\[z_1z_2=r_1r_2e^{i(\theta_1+\theta_2)}=r_1r_2\left(\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)\right)\quad\text{and}\quad \frac{z_1}{z_2}=\frac{r_1}{r_2}e^{i(\theta_1-\theta_2)}=\frac{r_1}{r_2}\left(\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)\right).\]

The division of course only if \(r_2\neq0\).

Fundamental theorem of algebra: For every polynomial \(p(x)\) of degree \(n\in\{1,2,3,\ldots\}\) we have that

\[p(x)=c(x-x_1)(x-x_2)\cdots(x-x_n)\quad\text{with}\quad c,x_1,x_2,\ldots,x_n\in\mathbb{C}.\]

If \(p(x)\) is a real polynomial (all coefficients are real), then nonreal zeros only occur in complex conjugate pairs.

In that case we have: if \(\alpha\in\mathbb{C}\), then \((z-\alpha)(z-\overline{\alpha})=z^2-(\alpha+\overline{\alpha})z+\alpha\overline{\alpha}=z^2-2\text{Re}(\alpha)z+|\alpha|^2\).

Examples: \(z^2-5z+6=(z-2)(z-3)\), \(z^3-3z^2+4z-2=(z-1)(z^2-2z+2)=(z-1)\left((z-1)^2+1\right)\), \(z^4-3z^2-4=(z^2-4)(z^2+1)=(z-2)(z+2)(z^2+1)\) and \(z^5-2z^4-z+2=(z-2)(z^4-1)=(z+1)(z-1)(z-2)(z^2+1)\).

For quadratic equations of the form \(az^2+bz+c=0\) we then have three possibilities:

1. \(D=b^2-ac > 0:\;z=\displaystyle\frac{-b\pm\sqrt{D}}{2a}\).


2. \(D=b^2-4ac = 0:\;z=-\displaystyle\frac{b}{2a}\;\text{(tweemaal)}\).


3. \(D=b^2-4ac < 0:\;z=\displaystyle\frac{-b\pm i\sqrt{-D}}{2a}\).

For powers of complex numbers we use the polar form:

Examples:

Since \(1+i=\sqrt{2}\,e^{\frac{1}{4}\pi i}\) and \(\sqrt{3}-i=2\,e^{-\frac{1}{6}\pi i}\), then we have:

\[\frac{(1+i)^6}{(\sqrt{3}-i)^2}=\frac{(\sqrt{2}\,e^{\frac{1}{4}\pi i})^6}{(2\,e^{-\frac{1}{6}\pi i})^3} =\frac{2^3}{2^3}\cdot\frac{e^{\frac{3}{2}\pi i}}{e^{-\frac{1}{2}\pi i}}=e^{2\pi i}=e^0=1.\]

Since \(1+i\sqrt{3}=2\,e^{\frac{1}{3}\pi i}\) and \(1-i=\sqrt{2}\,e^{-\frac{1}{4}\pi i}\), then we have:

\[\frac{(1+i\sqrt{3})^{25}}{(1-i)^{50}}=\frac{(2\,e^{\frac{1}{3}\pi i})^{25}}{(\sqrt{2}\,e^{-\frac{1}{4}\pi i})^{50}} =\frac{2^{25}}{2^{25}}\cdot\frac{e^{\frac{25}{3}\pi i}}{e^{-\frac{25}{2}\pi i}}=e^{\frac{125}{5}\pi i} =e^{\frac{5}{6}\pi i}=-\tfrac{1}{2}\sqrt{3}+\tfrac{1}{2}i.\]

Solve \(z^5=4-4i\). Suppose that \(z=r\,e^{\theta i}\), then we have:

\[z^5=4-4i\quad\Longleftrightarrow\quad r^5e^{5\theta i}=4\sqrt{2}\,e^{-\frac{1}{4}\pi i}\quad\Longleftrightarrow\quad r=\sqrt{2}\;\text{and}\;5\theta=-\tfrac{1}{4}\pi+2k\pi,\;k\in\mathbb{Z}.\]

Hence: \(r=\sqrt{2}\) and \(\theta=-\frac{1}{20}\pi+\frac{2}{5}k\pi\) with \(k\in\mathbb{Z}\).

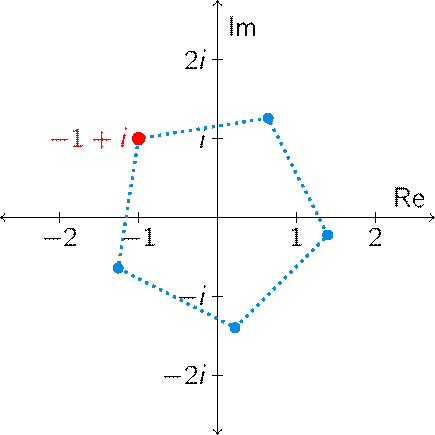Now we find the five different solutions
by choosing five consecutive values of \(k\):

1. \(k=0:\;\theta=-\frac{1}{20}\pi\;\Longrightarrow\;z_1=\sqrt{2}e^{-\frac{1}{20}\pi i}\),


2. \(k=1:\;\theta=-\frac{1}{20}\pi+\frac{2}{5}\pi=\frac{7}{20}\pi\;\Longrightarrow\;z_2=\sqrt{2}e^{\frac{7}{20}\pi i}\),


3. \(k=2:\;\theta=-\frac{1}{20}\pi+\frac{4}{5}\pi=\frac{15}{20}\pi=\frac{3}{4}\pi\;\Longrightarrow\;z_3=\sqrt{2}e^{\frac{3}{4}\pi i}=-1+i\),


4. \(k=3:\;\theta=-\frac{1}{20}\pi+\frac{6}{5}\pi=\frac{23}{20}\pi\;\Longrightarrow\;z_4=\sqrt{2}e^{\frac{23}{20}\pi i}=\sqrt{2}e^{-\frac{17}{20}\pi i}\),


5. \(k=4:\;\theta=-\frac{1}{20}\pi+\frac{8}{5}\pi=\frac{31}{20}\pi\;\Longrightarrow\;z_5=\sqrt{2}e^{\frac{31}{20}\pi i}=\sqrt{2}e^{-\frac{9}{20}\pi i}\).

---

Last modified on March 1, 2021