Lineaire Algebra – Symmetrische matrices en kwadratische vormen – Kwadratische vormen

Een aardige toepassing van symmetrische matrices treedt op in de theorie van kwadratische vormen.

Definitie: Een kwadratische vorm op \(\mathbb{R}^n\) is een functie \(Q:\mathbb{R}^n\to\mathbb{R}\) die voor elke vector \(\mathbf{x}\in\mathbb{R}^n\) geschreven kan worden als \(Q(x)=\mathbf{x}^TA\mathbf{x}\) met \(A\) een symmetrische \(n\times n\) matrix. Deze symmetrische matrix \(A\) heet de matrix van de kwadratische vorm \(Q\).

Voorbeelden:

1) \(A=\begin{pmatrix}7&2\\2&4\end{pmatrix}\): \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}=\begin{pmatrix}x_1&x_2\end{pmatrix} \begin{pmatrix}7&2\\2&4\end{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix}=7x_1^2+4x_1x_2+4x_2^2\).

2) \(Q(\mathbf{x})=x_1^2+2x_1x_2+3x_2^2=\mathbf{x}^TA\mathbf{x}\) met \(A=\begin{pmatrix}1&1\\1&3\end{pmatrix}\). Dus: \(A\) is de matrix van de kwadratische vorm \(Q\). Merk op dat ook geldt dat \(Q(\mathbf{x})=\mathbf{x}^TB\mathbf{x}\) met (bijvoorbeeld) \(B=\begin{pmatrix}1&2\\0&3\end{pmatrix}\), maar \(B\) is geen symmetrische matrix.

3) \(Q(\mathbf{x})=x_1^2+2x_2^2+3x_3^2+4x_1x_2-8x_1x_3-6x_2x_4=\mathbf{x}^TA\mathbf{x}\) met \(A=\begin{pmatrix}1&2&-4\\2&2&-3\\-4&-3&3\end{pmatrix}\). De coëfficiënten van de kwadraten komen op de hoofddiagonaal en de coëfficiënten van de zogenaamde kruisproducten worden netjes over twee plaatsen verdeeld zodat er een symmetrische matrix ontstaat. Deze matrix is dus uniek en heet daarom de matrix van de kwadratische vorm Q.

4) \(Q(\mathbf{x})=(x_1-2x_2)^2+4(x_1+x_3)^2+2(x_2-3x_3)^2\). Dan geldt:

\begin{align*} Q(\mathbf{x})&=x_1^2-4x_1x_2+4x_2^2+4x_1^2+8x_1x_3+4x_3^2+2x_2^2-12x_2x_3+18x_3^2\\[2.5mm] &=5x_1^2+6x_2^2+22x_3^2-4x_1x_2+8x_1x_3-12x_2x_3=\mathbf{x}^TA\mathbf{x}\quad\text{met}\quad A=\begin{pmatrix}5&-2&4\\-2&6&-6\\4&-6&22\end{pmatrix}. \end{align*}

Aan de eerste vorm zien we duidelijk dat \(Q(\mathbf{x})\geq0\). Verder zien we eenvoudig dat: \(Q(\mathbf{x})=0\;\Longleftrightarrow\;\mathbf{x}=\mathbf{0}\). Dus: \(Q(\mathbf{x})>0\) voor alle \(\mathbf{x}\neq\mathbf{0}\). Zo'n kwadratische vorm heet positief definiet. Merk op dat dit bij de laatste vorm niet evident is.

Definitie: Een kwadratische vorm heet

1. positief definiet als \(Q(\mathbf{x})>0\) voor alle \(\mathbf{x}\neq\mathbf{0}\);


2. negatief definiet als \(Q(\mathbf{x})<0\) voor alle \(\mathbf{x}\neq\mathbf{0}\);


3. indefiniet als \(Q(\mathbf{x})\) zowel positieve als negatieve waarden aanneemt.

Als \(Q(\mathbf{x})\geq0\) voor alle \(\mathbf{x}\), dan heet de kwadratische vorm \(Q\) positief semidefiniet en als \(Q(\mathbf{x})\leq0\) voor alle \(\mathbf{x}\), dan heet de kwadratische vorm \(Q\) negatief semidefiniet.

Voorbeelden:

1) \(Q(\mathbf{x})=-(x_1-x_2)^2-(x_1+2x_3)^2-2(x_2-4x_3)^2\) is negatief definiet.

2) \(Q(\mathbf{x})=-(x_1-x_2)^2-(x_1+2x_3)^2\) is negatief semidefiniet. Immers: er geldt (bijvoorbeeld) dat \(Q(\mathbf{x})=0\) voor \(\mathbf{x}=\begin{pmatrix}2\\2\\-1\end{pmatrix}\neq\mathbf{0}\).

3) \(Q(\mathbf{x})=(x_1+x_2)^2-2(x_1-x_3)^2\) is indefiniet, want \(Q(\mathbf{x})=1>0\) voor \(\mathbf{x}=\begin{pmatrix}1\\0\\1\end{pmatrix}\) en \(Q(\mathbf{x})=-2<0\) voor \(\mathbf{x}=\begin{pmatrix}1\\-1\\0\end{pmatrix}\).

4) \(Q(\mathbf{x})=x_1^2+6x_2^2+^22x_3^2+4x_1x_2-12x_2x_3\) is positief definiet, want:

\[Q(\mathbf{x})=(x_1+2x_2)^2+2x_2^2-12x_2x_3+22x_3^2=(x_1+2x_2)^2+2(x_2-3x_3)^2+4x_3^2.\]

Stel dat \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}\) met \(A\) een symmetrische matrix. Dan is \(A\) orthogonaal diagonaliseerbaar, dus: er bestaan een orthogonale matrix \(P\) en een diagonaalmatrix \(D\) zodat \(A=PDP^T\). Stel \(\mathbf{x}=P\mathbf{y}\), dan volgt:

\[Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}=(P\mathbf{y})^TAP\mathbf{y}=\mathbf{y}^TP^TAP\mathbf{y} =\mathbf{y}^TP^PDP^TP\mathbf{y}=\mathbf{y}^TD\mathbf{y}.\]

Omdat \(D\) een diagonaalmatrix is, \(D=\text{diag}(\lambda_1,\ldots,\lambda_n)\), bevat de laatste formule geen kruisproducten:

\[\mathbf{y}^TD\mathbf{y}=\lambda_1y_1^2+\cdots+\lambda_ny_n^2.\]

In deze vorm is gemakkelijk te zien of the kwadratische vorm positief (semi)definiet, negatief (semi)definiet of indefiniet is. Er geldt:

Stelling: Als \(A\) een symmetrische matrix is en \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}\), dan geldt:

1. De kwadratische vorm \(Q\) is positief definiet dan en slechts dan als alle eigenwaarden van \(A\) positief zijn;


2. De kwadratische vorm \(Q\) is negatief definiet dan en slechts dan als alle eigenwaarden van \(A\) negatief zijn;


3. De kwadratische vorm \(Q\) is indefiniet dan en slechts dan als \(A\) zowel positieve als negatieve eigenwaarden heeft.

Als alle eigenwaarden van \(A\) niet-negatief zijn, dan is de kwadratische vorm \(Q\) positief semedefiniet en als alle eigenwaarden van \(A\) niet-postief zijn, dan is de kwadratische vorm \(Q\) negatief definiet.

Door de transformatie \(\mathbf{x}=P\mathbf{y}\) kunnen we de kwadratische vorm \(Q(\mathbf{x}=\mathbf{x}^TA\mathbf{x}\) schrijven in de vorm \(\mathbf{y}^TD\mathbf{y}\) zonder kruisproducten. Dit heet het op hoofdassen brengen van de kwadratische vorm. De kolommen van de matrix \P\) worden wel de hoofdassen van de kwadratische vorm genoemd. Deze termininologie wordt verklaard door de volgende voorbeelden:

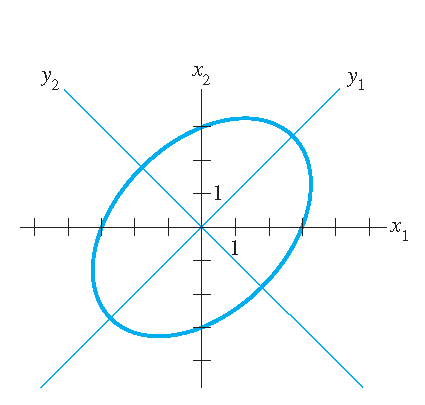
1) Beschouw de vergelijking \(5x_1^2-4x_1x_2+5x_2^2=48\). Dit kan geschreven worden als \(\mathbf{x}^TA\mathbf{x}=48\) met \(A=\begin{pmatrix}5&-2\\-2&5\end{pmatrix}\). Dan volgt:

\[|A-\lambda I|=\begin{vmatrix}5-\lambda&-2\\-2&5-\lambda\end{vmatrix}=\lambda^2-10\lambda+21=(\lambda-7)(\lambda-3).\]

Verder volgt:

\[\lambda_1=7:\quad\begin{pmatrix}-2&-2\\-2&-2\end{pmatrix}\sim\begin{pmatrix}1&1\\0&0\end{pmatrix}\quad\Longrightarrow\quad \mathbf{u}_1=\frac{1}{\sqrt{2}}\begin{pmatrix}-1\\1\end{pmatrix}\]

en

\[\lambda_2=3:\quad\begin{pmatrix}2&-2\\-2&2\end{pmatrix}\sim\begin{pmatrix}1&-1\\0&0\end{pmatrix}\quad\Longrightarrow\quad \mathbf{u}_2=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\1\end{pmatrix}.\]

De vergelijking is dus equivalent met \(7y_1^2+3y_2^2=48\), waarbij \(\mathbf{x}=P\mathbf{y}\) met \(P=\Bigg(\mathbf{u}_1\;\mathbf{u}_2\Bigg) =\dfrac{1}{\sqrt{2}}\begin{pmatrix}-1&1\\1&1\end{pmatrix}\). Dit leidt tot de volgende ellips:

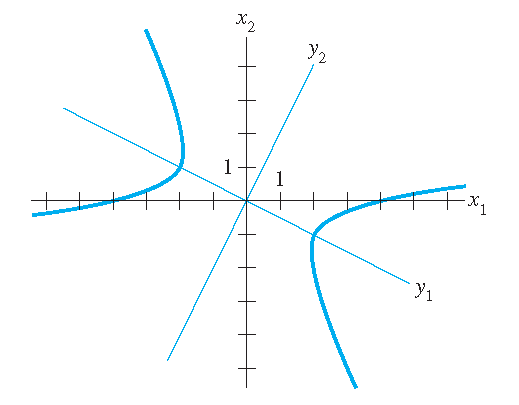
2) Beschouw de vergelijking \(x_1^2-8x_1x_2-5x_2^2=16\). Dit kan geschreven worden als \(\mathbf{x}^TA\mathbf{x}=16\) met \(A=\begin{pmatrix}1&-4\\-4&-5\end{pmatrix}\). Dan volgt:

\[|A-\lambda I|=\begin{vmatrix}1-\lambda&-4\\-4&-5-\lambda\end{vmatrix}=\lambda^2+4\lambda-21=(\lambda-3)(\lambda+7).\]

Verder volgt:

\[\lambda_1=3:\quad\begin{pmatrix}-2&-4\\-4&-8\end{pmatrix}\sim\begin{pmatrix}1&2\\0&0\end{pmatrix}\quad\Longrightarrow\quad \mathbf{u}_1=\frac{1}{\sqrt{5}}\begin{pmatrix}-2\\1\end{pmatrix}\]

en

\[\lambda_2=-7:\quad\begin{pmatrix}8&-4\\-4&2\end{pmatrix}\sim\begin{pmatrix}2&-1\\0&0\end{pmatrix}\quad\Longrightarrow\quad \mathbf{u}_2=\frac{1}{\sqrt{5}}\begin{pmatrix}1\\2\end{pmatrix}.\]

De vergelijking is dus equivalent met \(3y_1^2-7y_2^2=16\), waarbij \(\mathbf{x}=P\mathbf{y}\) met \(P=\Bigg(\mathbf{u}_1\;\mathbf{u}_2\Bigg) =\dfrac{1}{\sqrt{5}}\begin{pmatrix}-2&1\\1&2\end{pmatrix}\). Dit leidt tot de volgende hyperbool:

Voorbeelden:

1) De kwadratische vorm \(Q(\mathbf{x})=7x_1^2+4x_1x_2+4x_2^2\) is positief definiet, want \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}\) met \(A=\begin{pmatrix}7&2\\2&4\end{pmatrix}\) en die heeft de eigenwaarden \(\lambda_1=8\) en \(\lambda_2=3\).

2) De kwadratische vorm \(Q(\mathbf{x})=5x_1^2+5x_2^2+2x_3^2-8x_1x_2-4x_1x_3+4x_2x_3\) is positief definiet, want \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}\) met \(A=\begin{pmatrix}5&-4&-2\\-4&5&2\\-2&2&2\end{pmatrix}\) en die heeft de eigenwaarden \(\lambda_1=10\) (eenmaal) en \(\lambda_2=1\) (tweemaal).

3) De kwadratische vorm \(Q(\mathbf{x})=\mathbf{x}^TB\mathbf{x}\) met \(B=\begin{pmatrix}1&2&6\\0&3&2\\0&0&1\end{pmatrix}\) is indefiniet. Merk op dat \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}\) met \(A=\begin{pmatrix}1&1&3\\1&3&1\\3&1&1\end{pmatrix}\) een symmetrische matrix. Dus: \(A\) is de matrix van de kwadratische vorm \(Q\) (niet \(B\)). Nu geldt:

\begin{align*} |A-\lambda I|&=\begin{vmatrix}1-\lambda&1&3\\1&3-\lambda&1\\3&1&1-\lambda\end{vmatrix}=\begin{vmatrix}-2-\lambda&0&2+\lambda\\ 1&3-\lambda&1\\3&1&1-\lambda\end{vmatrix}=\begin{vmatrix}-2-\lambda&0&0\\1&3-\lambda&2\\3&1&4-\lambda\end{vmatrix}\\[2.5mm] &=(-2-\lambda)\begin{vmatrix}3-\lambda&2\\1&4-\lambda\end{vmatrix}=-(\lambda+2)(\lambda^2-7\lambda+10)=-(\lambda+2)(\lambda-2)(\lambda-5). \end{align*}

De eigenwaarden van \(A\) zijn dus: \(\lambda_1=5\), \(\lambda_2=2\) en \(\lambda_3=-2\). Merk op dat de eigenwaarden van \(B\) dus blijkbaar niets zeggen over de kwadratische vorm \(Q\).

---

Laatst gewijzigd op 2 mei 2021