Linear Algebra – Symmetric matrices and quadratic forms – Quadratic forms

A nice application of symmetric matrices occurs at the theory of quadratic forms.

Definition: A quadratic form on \(\mathbb{R}^n\) is a function \(Q:\mathbb{R}^n\to\mathbb{R}\) that for each vector \(\mathbf{x}\in\mathbb{R}^n\) can be written as \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}\) with \(A\) a symmetric \(n\times n\) matrix. This symmetric matrix \(A\) is called the matrix of the quadratic form \(Q\).

Examples:

1) \(A=\begin{pmatrix}7&2\\2&4\end{pmatrix}\): \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}=\begin{pmatrix}x_1&x_2\end{pmatrix} \begin{pmatrix}7&2\\2&4\end{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix}=7x_1^2+4x_1x_2+4x_2^2\).

2) \(Q(\mathbf{x})=x_1^2+2x_1x_2+3x_2^2=\mathbf{x}^TA\mathbf{x}\) with \(A=\begin{pmatrix}1&1\\1&3\end{pmatrix}\). Hence: \(A\) is the matrix of the quadratic form \(Q\). Note that we also have that \(Q(\mathbf{x})=\mathbf{x}^TB\mathbf{x}\) with (for instance) \(B=\begin{pmatrix}1&2\\0&3\end{pmatrix}\), however \(B\) is not a symmetric matrix.

3) \(Q(\mathbf{x})=x_1^2+2x_2^2+3x_3^2+4x_1x_2-8x_1x_3-6x_2x_4=\mathbf{x}^TA\mathbf{x}\) with \(A=\begin{pmatrix}1&2&-4\\2&2&-3\\-4&-3&3\end{pmatrix}\). The coefficients of the squares appear on the main diagonal and the coefficients of the so-called cross-product terms are neatly divided among two positions such that a symmetric matrix arises. Hence this matrix is unique and is therefore called the matrix of the quadratic form Q.

4) \(Q(\mathbf{x})=(x_1-2x_2)^2+4(x_1+x_3)^2+2(x_2-3x_3)^2\). Then we have:

\begin{align*} Q(\mathbf{x})&=x_1^2-4x_1x_2+4x_2^2+4x_1^2+8x_1x_3+4x_3^2+2x_2^2-12x_2x_3+18x_3^2\\[2.5mm] &=5x_1^2+6x_2^2+22x_3^2-4x_1x_2+8x_1x_3-12x_2x_3=\mathbf{x}^TA\mathbf{x}\quad\text{with}\quad A=\begin{pmatrix}5&-2&4\\-2&6&-6\\4&-6&22\end{pmatrix}. \end{align*}

The first form easily shows that \(Q(\mathbf{x})\geq0\). Moreover, we easily see that: \(Q(\mathbf{x})=0\;\Longleftrightarrow\;\mathbf{x}=\mathbf{0}\). Hence: \(Q(\mathbf{x})>0\) for all \(\mathbf{x}\neq\mathbf{0}\). Such a quadratic form is called positive definite. Note that this is not evident from the latter form.

Definition: A quadratic form is called

1. positive definite if \(Q(\mathbf{x})>0\) for all \(\mathbf{x}\neq\mathbf{0}\);


2. negative definite if \(Q(\mathbf{x})<0\) for all \(\mathbf{x}\neq\mathbf{0}\);


3. indefinite if \(Q(\mathbf{x})\) attains both positive and negative values.

If \(Q(\mathbf{x})\geq0\) for all \(\mathbf{x}\), then the quadratic form \(Q\) is called positive semidefinite and if \(Q(\mathbf{x})\leq0\) for all \(\mathbf{x}\), then the quadratic form \(Q\) is called negative semidefinite.

Examples:

1) \(Q(\mathbf{x})=-(x_1-x_2)^2-(x_1+2x_3)^2-2(x_2-4x_3)^2\) is negative definite.

2) \(Q(\mathbf{x})=-(x_1-x_2)^2-(x_1+2x_3)^2\) is negative semidefinite. Indeed: we have (for instance) that \(Q(\mathbf{x})=0\) for \(\mathbf{x}=\begin{pmatrix}2\\2\\-1\end{pmatrix}\neq\mathbf{0}\).

3) \(Q(\mathbf{x})=(x_1+x_2)^2-2(x_1-x_3)^2\) is indefinite, since \(Q(\mathbf{x})=1>0\) for \(\mathbf{x}=\begin{pmatrix}1\\0\\1\end{pmatrix}\) and \(Q(\mathbf{x})=-2<0\) for \(\mathbf{x}=\begin{pmatrix}1\\-1\\0\end{pmatrix}\).

4) \(Q(\mathbf{x})=x_1^2+6x_2^2+^22x_3^2+4x_1x_2-12x_2x_3\) is positive definite, since:

\[Q(\mathbf{x})=(x_1+2x_2)^2+2x_2^2-12x_2x_3+22x_3^2=(x_1+2x_2)^2+2(x_2-3x_3)^2+4x_3^2.\]

Let \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}\) with \(A\) a symmetric matrix. Then is \(A\) orthogonally diagonizable, so: there exist an orthogonal matrix \(P\) and a diagonal matrix \(D\) such that \(A=PDP^T\). Let \(\mathbf{x}=P\mathbf{y}\), then we have:

\[Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}=(P\mathbf{y})^TAP\mathbf{y}=\mathbf{y}^TP^TAP\mathbf{y} =\mathbf{y}^TP^PDP^TP\mathbf{y}=\mathbf{y}^TD\mathbf{y}.\]

Since \(D\) is a diagonal matrix, \(D=\text{diag}(\lambda_1,\ldots,\lambda_n)\), the latter formula does not contain any cross-product terms:

\[\mathbf{y}^TD\mathbf{y}=\lambda_1y_1^2+\cdots+\lambda_ny_n^2.\]

From this form it is easily seen whether the quadratic form is positive (semi)definite, negative (semi)definite or indefinite. We have:

Theorem: If \(A\) is a symmetric matrix and \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}\), then we have:

1. The quadratic form \(Q\) is positive definite if and only if all eigenvalues of \(A\) are positive;


2. The quadratic form \(Q\) is negative definite if and only if all eigenvalues of \(A\) are negative;


3. The quadratic form \(Q\) is indefinite if and only if \(A\) has both positive and negative eigenvalues.

If all eigenvalues of \(A\) are nonnegative, then the quadratic form \(Q\) is positive semidefinite and if all eigenvalues of \(A\) are nonpositive, then the quadratic form \(Q\) is negative semidefinite.

Using the change of variable \(\mathbf{x}=P\mathbf{y}\) we can transform the quadratic form \(Q(\mathbf{x}=\mathbf{x}^TA\mathbf{x}\) to the form \(\mathbf{y}^TD\mathbf{y}\) without cross-product terms. This is called the principal axes form of the quadratic form. The columns of the matrix \P\) are called the principal axes of the quadratic form. This terminology is explained in the following examples:

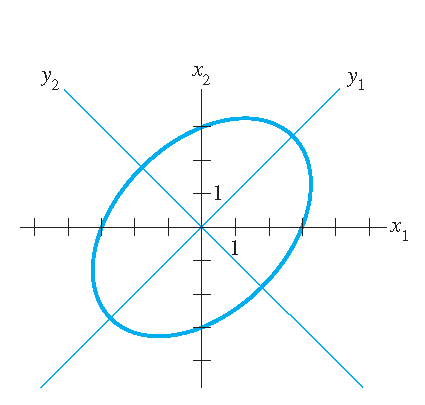
1) Consider the equation \(5x_1^2-4x_1x_2+5x_2^2=48\). This can be written as \(\mathbf{x}^TA\mathbf{x}=48\) with \(A=\begin{pmatrix}5&-2\\-2&5\end{pmatrix}\). Then we have:

\[|A-\lambda I|=\begin{vmatrix}5-\lambda&-2\\-2&5-\lambda\end{vmatrix}=\lambda^2-10\lambda+21=(\lambda-7)(\lambda-3).\]

Moreover, we have:

\[\lambda_1=7:\quad\begin{pmatrix}-2&-2\\-2&-2\end{pmatrix}\sim\begin{pmatrix}1&1\\0&0\end{pmatrix}\quad\Longrightarrow\quad \mathbf{u}_1=\frac{1}{\sqrt{2}}\begin{pmatrix}-1\\1\end{pmatrix}\]

and

\[\lambda_2=3:\quad\begin{pmatrix}2&-2\\-2&2\end{pmatrix}\sim\begin{pmatrix}1&-1\\0&0\end{pmatrix}\quad\Longrightarrow\quad \mathbf{u}_2=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\1\end{pmatrix}.\]

So the equation is equivalent to \(7y_1^2+3y_2^2=48\), where \(\mathbf{x}=P\mathbf{y}\) with \(P=\Bigg(\mathbf{u}_1\;\mathbf{u}_2\Bigg) =\dfrac{1}{\sqrt{2}}\begin{pmatrix}-1&1\\1&1\end{pmatrix}\). This leads to the following ellipse:

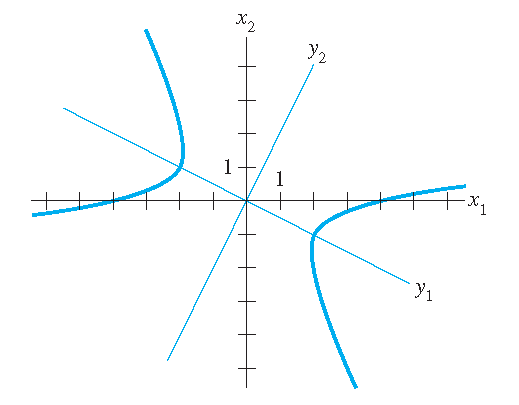
2) Consider the equation \(x_1^2-8x_1x_2-5x_2^2=16\). This can be written as \(\mathbf{x}^TA\mathbf{x}=16\) with \(A=\begin{pmatrix}1&-4\\-4&-5\end{pmatrix}\). Then we have:

\[|A-\lambda I|=\begin{vmatrix}1-\lambda&-4\\-4&-5-\lambda\end{vmatrix}=\lambda^2+4\lambda-21=(\lambda-3)(\lambda+7).\]

Moreover, we have:

\[\lambda_1=3:\quad\begin{pmatrix}-2&-4\\-4&-8\end{pmatrix}\sim\begin{pmatrix}1&2\\0&0\end{pmatrix}\quad\Longrightarrow\quad \mathbf{u}_1=\frac{1}{\sqrt{5}}\begin{pmatrix}-2\\1\end{pmatrix}\]

and

\[\lambda_2=-7:\quad\begin{pmatrix}8&-4\\-4&2\end{pmatrix}\sim\begin{pmatrix}2&-1\\0&0\end{pmatrix}\quad\Longrightarrow\quad \mathbf{u}_2=\frac{1}{\sqrt{5}}\begin{pmatrix}1\\2\end{pmatrix}.\]

So the equation is equivalent to \(3y_1^2-7y_2^2=16\), where \(\mathbf{x}=P\mathbf{y}\) with \(P=\Bigg(\mathbf{u}_1\;\mathbf{u}_2\Bigg) =\dfrac{1}{\sqrt{5}}\begin{pmatrix}-2&1\\1&2\end{pmatrix}\). This leads to the following hyperbola:

Examples:

1) The quadratic form \(Q(\mathbf{x})=7x_1^2+4x_1x_2+4x_2^2\) is positive definite, since \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}\) with \(A=\begin{pmatrix}7&2\\2&4\end{pmatrix}\) which has eigenvales \(\lambda_1=8\) and \(\lambda_2=3\).

2) The quadratic form \(Q(\mathbf{x})=5x_1^2+5x_2^2+2x_3^2-8x_1x_2-4x_1x_3+4x_2x_3\) is positive definite, since \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}\) with \(A=\begin{pmatrix}5&-4&-2\\-4&5&2\\-2&2&2\end{pmatrix}\) which has eigenvales \(\lambda_1=10\) (once) and \(\lambda_2=1\) (twice).

3) The quadratic form \(Q(\mathbf{x})=\mathbf{x}^TB\mathbf{x}\) with \(B=\begin{pmatrix}1&2&6\\0&3&2\\0&0&1\end{pmatrix}\) is indefinite. Note that \(Q(\mathbf{x})=\mathbf{x}^TA\mathbf{x}\) with \(A=\begin{pmatrix}1&1&3\\1&3&1\\3&1&1\end{pmatrix}\) a symmetric matrix. So, \(A\) is the matrix of the quadratic form \(Q\) (not \(B\)). Now we have:

\begin{align*} |A-\lambda I|&=\begin{vmatrix}1-\lambda&1&3\\1&3-\lambda&1\\3&1&1-\lambda\end{vmatrix}=\begin{vmatrix}-2-\lambda&0&2+\lambda\\ 1&3-\lambda&1\\3&1&1-\lambda\end{vmatrix}=\begin{vmatrix}-2-\lambda&0&0\\1&3-\lambda&2\\3&1&4-\lambda\end{vmatrix}\\[2.5mm] &=(-2-\lambda)\begin{vmatrix}3-\lambda&2\\1&4-\lambda\end{vmatrix}=-(\lambda+2)(\lambda^2-7\lambda+10)=-(\lambda+2)(\lambda-2)(\lambda-5). \end{align*}

So, the eigenvalues of \(A\) are: \(\lambda_1=5\), \(\lambda_2=2\) and \(\lambda_3=-2\). Note that the eigenvalues of \(B\) apparently do not say anything about the quadratic form \(Q\).

---

Last modified on May 2, 2021