Differentiaalvergelijkingen – Niet-lineaire differentiaalvergelijkingen – Autonome stelsels

We beschouwen autonome stelsels van de vorm

\[\frac{dx}{dt}=F(x,y)\quad\text{en}\quad\frac{dy}{dt}=G(x,y),\]

waarbij \(F\) en \(G\) dus alleen van \(x\) en \(y\) afhangen en niet expliciet van \(t\).

Een punt \((x_0,y_0)\) heet een kritiek punt of stationair punt van het stelsel als zowel \(F(x_0,y_0)=0\) als \(G(x_0,y_0)=0\). Het stelsel heet lokaal lineair in zo'n kritiek punt \((x_0,y_0)\) als \(F\) en \(G\) continue tweede orde partiële afgeleiden hebben in \((x_0,y_0)\). In dat geval zijn

\[F(x_0,y_0)+F_x(x_0,y_0)(x-x_0)+F_y(x_0,y_0)\]

en

\[G(x_0,y_0)+G_x(x_0,y_0)(x-x_0)+G_y(x_0,y_0)(y-y_0)\]

goede benaderingen van \(F(x,y)\) en \(G(x,y)\) respectievelijk. Dan geldt dus:

\[F(x,y)\approx F(x_0,y_0)+F_x(x_0,y_0)(x-x_0)+F_y(x_0,y_0)\]

en

\[G(x,y)\approx G(x_0,y_0)+G_x(x_0,y_0)(x-x_0)+G_y(x_0,y_0)(y-y_0)\]

in de buurt van het kritieke punt \((x_0,y_0)\). Aangezien \((F(x_0,y_0)=0\) en \(G(x_0,y_0)=0\), volgt dan:

\[\frac{d}{dt}\begin{pmatrix}x-x_0\\y-y_0\end{pmatrix}\approx\begin{pmatrix}F_x(x_0,y_0) & F_y(x_0,y_0)\\G_x(x_0,y_0) & G_y(x_0,y_0)\end{pmatrix} \begin{pmatrix}x-x_0\\y-y_0\end{pmatrix}.\]

Dit betekent dat het gedrag van de oplossingen rond zo'n kritiek of stationair punt \((x_0,y_0)\) vergelijkbaar is met het gedrag van de oplossingen van het bijbehorende lineaire stelsel (rond de oorsprong). De matrix

\[\begin{pmatrix}F_x(x,y) & F_y(x,y)\\G_x(x,y) & G_y(x,y)\end{pmatrix}\]

heet de Jacobi matrix van het stelsel.

Uitzonderingen:

Het gedrag van de oplossingen van het lineaire stelsel kunnen we aflezen uit de eigenwaarden (en eigenvectoren) van de matrix

\[\begin{pmatrix}F_x(x_0,y_0)&F_y(x_0,y_0)\\G_x(x_0,y_0)&G_y(x_0,y_0)\end{pmatrix}.\]

Er zijn twee uitzonderingen:

1. \(r_1=r_2=r\in\mathbb{R}\): de oorsprong \(O\) in het lineaire stelsel is dan een zuivere of een onzuivere knoop. In het niet-lineaire stelsel kan het kritieke of stationaire punt \((x_0,y_0)\) dan ook een spiraalpunt zijn (de stabiliteit wordt bepaald door het teken van \(r\)).


2. \(r_{1,2}=\pm i\beta\) met \(\beta\in\mathbb{R}\): de oorsprong \(O\) in het lineaire stelsel is dan een centerpunt. In het niet-lineaire stelsel kan het kritieke of stationaire punt \((x_0,y_0)\) ook een spiraalpunt zijn (met onbekende stabiliteit).

Voorbeelden:

1) \(\displaystyle\frac{dx}{dt}=4-2y\) en \(\displaystyle\frac{dy}{dt}=12-3x^2\). De kritieke/stationaire punten zijn \((\pm2,2)\). De Jacobi matrix is \(J(x,y)=\begin{pmatrix}0&-2\\-6x&0\end{pmatrix}\).

Nu is \(J(-2,2)=\begin{pmatrix}0&-2\\12&0\end{pmatrix}\) met eigenwaarden \(\pm2i\sqrt{6}\). Dus: \((-2,2)\) is een center- of spiraalpunt met onbekende stabiliteit.

Verder volgt dat \(J(2,2)=\begin{pmatrix}0&-2\\-12&0\end{pmatrix}\) met eigenwaarden \(\pm2\sqrt{6}\). Dus: \((2,2)\) is een instabiel zadelpunt.

In dit geval geldt dat \(\displaystyle\frac{dy}{dx}=\frac{12-3x^2}{4-2y}\) separabel is met impliciete oplossing \(4y-y^2-12x+x^3=c\) met \(c\) een willekeurige constante. Voor enkele waarden van \(c\) zijn deze oplossingen te zien in het volgende plaatje:

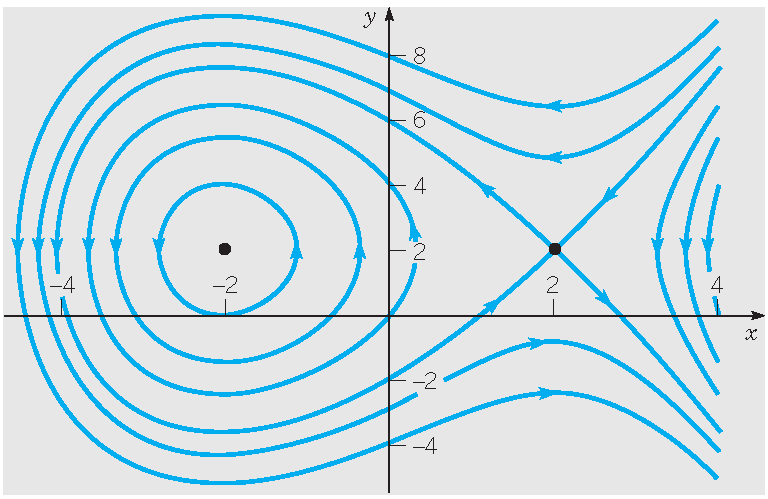
De kromme (met \(c=-12\)) die vanuit het zadelpunt \((2,2)\) naar links wegloopt en uiteindelijk terugkeert in \((2,2)\) wordt een separatrix genoemd.

2) \(\displaystyle\frac{dx}{dt}=-(x-y)(1-x-y)\) en \(\displaystyle\frac{dy}{dt}=x(2+y)\). Voor de kritieke/stationaire punten geldt:

\[\left\{\begin{array}{r}-(x-y)(1-x-y)=0\\[2.5mm]x(2+y)=0\end{array}\right.\quad\Longrightarrow\quad(0,0),\;\;(0,1),\;\;(-2,-2),\;\;(3,-2).\]

De Jacobi matrix is \(J(x,y)=\begin{pmatrix}2x-1&1-2y\\2+y&x\end{pmatrix}\).

Dus: \(J(0,0)=\begin{pmatrix}-1&1\\2&0\end{pmatrix}\) met eigenwaarden \(-2\) en \(1\). Dus: \((0,0)\) is een instabiel zadelpunt.

Verder is \(J(0,1)=\begin{pmatrix}-1&-1\\3&0\end{pmatrix}\) met eigenwaarden \(-\frac{1}{2}\pm\frac{1}{2}i\sqrt{11}\). Dus: \((0,1)\) is een asymptotisch stabiel spiraalpunt.

En \(J(-2,-2)=\begin{pmatrix}-5&5\\0&-2\end{pmatrix}\) met eigenwaarden \(-5\) en \(-2\). Dus: \((-2,-2)\) is een asymptotisch stabiele knoop.

Ten slotte is \(J(3,-2)=\begin{pmatrix}5&5\\0&3\end{pmatrix}\) met eigenwaarden \(3\) en \(5\). Dus: \((3,-2)\) is een instabiele knoop.

3) \(\displaystyle\frac{dx}{dt}=(2-y)(2x-y)\) en \(\displaystyle\frac{dy}{dt}=(2+x)(x-2y)\). Voor de kritieke/stationaire punten geldt:

\[\left\{\begin{array}{r}(2-y)(2x-y)=0\\[2.5mm](2+x)(x-2y)=0\end{array}\right.\quad\Longrightarrow\quad(0,0),\;\;(-2,-4),\;\;(-2,2),\;\;(4,2).\]

De Jacobi matrix is \(J(x,y)=\begin{pmatrix}2(2-y)&-2x+2y-2\\2x-2y+2&-2(2+x)\end{pmatrix}\).

Dus: \(J(0,0)=\begin{pmatrix}4&-2\\2&-4\end{pmatrix}\) met eigenwaarden \(\pm2\sqrt{3}\). Dus: \((0,0)\) is een instabiel zadelpunt.

Verder is \(J(-2,-4)=\begin{pmatrix}12&-6\\6&0\end{pmatrix}\) met dubbele eigenwaarde \(6\). Dus: \((-2,-4)\) is een instabiele knoop of een instabiel spiraalpunt.

En \(J(-2,2)=\begin{pmatrix}0&6\\-6&0\end{pmatrix}\) met eigenwaarden \(\pm6i\). Dus: \((-2,2)\) is een center- of spiraalpunt met onbekende stabiliteit.

Ten slotte is \(J(4,2)=\begin{pmatrix}0&-6\\6&-12\end{pmatrix}\) met dubbele eigenwaarde \(-6\). Dus: \((4,2)\) is een asymptotisch stabiele knoop of een asymptotisch stabiel spiraalpunt.

---

Laatst gewijzigd op 16 augustus 2021